A Regra da Cadeia Para Funções de Várias Variáveis

A Regra da Cadeia, em geral, nos diz como calcular a derivada de uma composição de funções. Nesse artigo queremos estabelecer o conceito de Regra da Cadeia para Funções de Várias Variáveis a Valores Reais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar.

Vamos apresentar esse conceito através de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.

A Regra da Cadeia

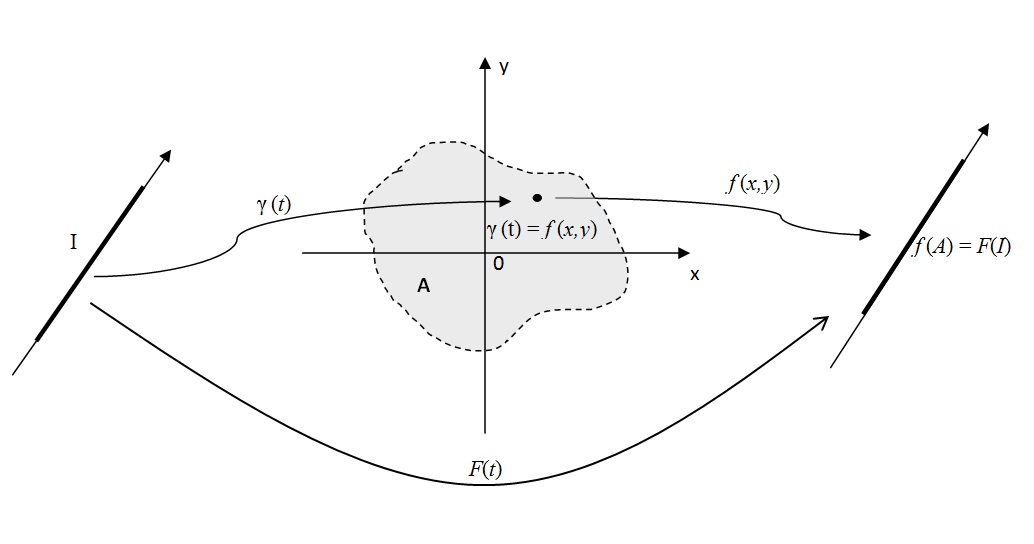
A regra da cadeia é a maneira de definir a diferenciabilidade de funções compostas. Considere f:A \subset \mathbb{R}^2 \rightarrow \mathbb{R}, A um suconjunto aberto do plano, e \gamma: I \rightarrow \mathbb{R}^2, tais que \gamma(t) \in A para todo intervalo I.

Então a composição é dada por F : \mathbb{R} e definida por f(\gamma(t)).

EXEMPLO

Sejam f(x,y) = xy e \gamma (t) = \left( t^3 , t^2 \right).

Vamos calcular F(t) = f(\gamma (t)):

Observe que: $$F(t) = f(\gamma (t)) = f \left( t^3 , t^2 \right) = t^5$$

Agora, vamos verificar se F'(t) = \nabla f \left(\gamma (t) \right). \gamma ` (t).

Primeiro, temos que F'(t) = 5t^4.

Em seguida, $$\nabla f \left( x,y \right) = \left( y , x \right) \Rightarrow \nabla f \left( t^3, t^2 \right) = \left( t^2 , t^3 \right) $$ e $$ \gamma ` (t) = \left( 3t^2 , 2t \right). $$ Assim, $$\nabla f \left(\gamma (t) \right). \gamma ` (t) = \left( t^2 , t^3 \right) . \left( 3t^2 , 2t \right) = 3t^4+2t^4 = 5t^4.$$

Portanto, F'(t) = \nabla f \left(\gamma (t) \right). \gamma ` (t).

TEOREMA (A REGRA DA CADEIA)

Sejam f:A \subset \mathbb{R}^2 \rightarrow \mathbb{R}, A um suconjunto aberto do plano, e \gamma: I \rightarrow \mathbb{R}^2, tais que \gamma(t) \in A para todo intervalo I. Nestas condições, se \gamma for derivável em t_0 e f em (x_0,y_0) = \gamma(t_0), então a composta F : \mathbb{R} \rightarrow \mathbb{R}, dada por F(t)= f(\gamma(t)) é diferenciável em t_0 e vale a regra da cadeia $$F'(t_0) = \nabla f \left(\gamma (t_0) \right). \gamma ` (t_0).$$

Segue deste teorema que se f for diferenciável em um conjunto aberto A do plano e \gamma derivável em I, então a composta F(t) = f\left( \gamma (t) \right) será diferenciável e, para todo t, $$F'(t) = \nabla f \left(\gamma (t) \right). \gamma `(t).$$

Fazendo \gamma (t) = \left( x(t), y(t) \right) e lembrando que $$\nabla f \left( x,y \right) = \left( \frac{\partial f}{\partial x} (x(t),y(t)) , \frac{\partial f}{\partial y} (x(t),y(t)) \right) = $$ e $$ \gamma `(t) = \left( \frac{dx}{dt}, \frac{dy}{dt} \right) $$

resulta:

$$\frac{dF}{dt} (t)= \frac{\partial f}{\partial x} (x(t),y(t)) \frac{dx}{dt} + \frac{\partial f}{\partial y} (x(t),y(t)) \frac{dy}{dt}$$ e na notação clássica $$\frac{dF}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}.$$

Com frequência, temos a função composta dada por z=f(x(t),y(t)) e pede, calcular-se \frac{dz}{dt}.

Assim, $$\frac{dz}{dt} = \frac{d}{dt}\left[ f(x,y) \right] = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}.$$

EXEMPLO

Sejam z=x^2y, x=e^{t^2} e y=2t+1. Calcule \frac{dz}{dt}.

Pelo teorema,

\begin{eqnarray*}
\frac{dz}{dt} & = & \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}\\
& = & \frac{\partial }{\partial x}(x^2y) \frac{d}{dt} \left( e^{t^2} \right) + \frac{\partial }{\partial y} (x^2y) \frac{d}{dt} (2t+1)\\
& = & 2xy(2t e^{t^2})+x^2(2t+1)\\
& = & 2e^{t^2}(2t+1)(2t e^{t^2})+\left( e^{t^2} \right)^2(2t+1)\\
\end{eqnarray*}

\begin{eqnarray*}
\frac{dz}{dt} & = & \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}\\
& = & \frac{\partial }{\partial x}(x^2y) \frac{d}{dt} \left( e^{t^2} \right) + \frac{\partial }{\partial y} (x^2y) \frac{d}{dt} (2t+1)\\
& = & 2xy(2t e^{t^2})+x^2(2t+1)\\
& = & 2e^{t^2}(2t+1)(2t e^{t^2})+\left( e^{t^2} \right)^2(2t+1)\\
\end{eqnarray*}

EXEMPLO

Seja F(t) = f\left( e^{t^2} , \sin(t) \right), sendo f(x,y) uma função diferenciável em \mathbb{R}^2.

Vamos expressar F'(t) em termos das derivadas parciais de f.

$$\frac{dF}{dt} (t)= \frac{\partial f}{\partial x} \left( e^{t^2} , \sin(t) \right) 2te^{t^2} + \frac{\partial f}{\partial y} \left( e^{t^2} , \sin(t) \right) \cos{t}$$

Sabendo que \frac{\partial f}{\partial y}(1,0) = 5, calculemos F'(0).

$$\frac{dF}{dt} (0)= \frac{\partial f}{\partial x} \left( 1 , 0 \right) 2.0.e^{0^2} + \frac{\partial f}{\partial y} \left( 1 , 0 \right) \cos{0} = 1. 5 = 5$$

A REGRA DA CADEIA PARA A COMPOSIÇÃO DE FUNÇÕES DE VÁRIAS VARIÁVEIS

Sejam A e B conjuntos abertos em \mathbb{R}^2 e sejam z=f(u,v) uma função que tem derivadas parciais de primeira ordem contínuas em A, u=u(x,y) e v=v(x,y) funções diferenciáveis em B tais que para todo (x,y) \in B tais que para todo (x,y) \in B temos que \left( u(x,y) , v(x,y) \right) \in A.

Seja a função composta $$h(x,y) = f\left( u(x,y) , v(x,y) \right),\;\;\;\;(x,y)\in B.$$

Então a função composta h(x,y) é diferenciável para todo (x,y) \in B, valendo:
$$\frac{\partial h}{\partial x} = \frac{\partial f}{\partial u} . \frac{\partial u}{\partial x} + \frac{\partial f}{\partial v} . \frac{\partial v}{\partial x}$$
$$\frac{\partial h}{\partial y} = \frac{\partial f}{\partial u} . \frac{\partial u}{\partial y} + \frac{\partial f}{\partial v} . \frac{\partial v}{\partial y}$$ que na forma matricial é dada por

$$\left[ \begin{array}{lr}
\frac{\partial h}{\partial x} & \frac{\partial h}{\partial y} \end{array} \right] = \left[ \begin{array}{lr}
\frac{\partial f}{\partial u} & \frac{\partial f}{\partial v} \end{array} \right] . \left[ \begin{array}{rl}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}\\
\\
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{array} \right]$$

EXEMPLO

Considere h(x,y) = f\left( x+y , x^2y-1 \right) com f(u^2 - v + 4). Encontre as derivadas parcias de h.

$$\frac{\partial h}{\partial x} \left( x , y \right) = 2 u . 1 + -1 . 2xy = 2(x+y) -2xy = 2x + 2y -2xy$$

$$\frac{\partial h}{\partial y} \left( x , y \right) = 2u . 1 + -1 . x^2 = 2(x+y) – x^2$$

A regra da cadeia pode ser generalizada e os exemplos a seguir mostram a sistemática utilizada.

EXEMPLO

Considere a função f(x,y,z)=x^2+y^2+z^2-1 e x(t)=\sin{t}, y(t) = \cos{t} e z(t)=t. Encontre \frac{df}{dt}.

Pela regra da cadeia,

$$\frac{df}{dt} = \frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt} + \frac{\partial f}{\partial z}\frac{dz}{dt} = $$ $$= 2x. (\cos{t}) + 2y(-\sin{t})+1.2z=2\sin{t}\cos{t}- 2\cos{t}\sin{t}+ 2t = 2t $$

EXEMPLO

Seja z=f\left( r^2+s^2-t , rst \right) onde f(x,y) é uma função diferenciável. Encontrar \frac{\partial z}{\partial r}, \frac{\partial z}{\partial s} e \frac{\partial z}{\partial t} em termos das derivadas parcias de f.

Temos que z=f\left( r^2+s^2-t , rst \right) com x(t)=r^2 +s^2 - t e y(t) = rst. Pela regra da cadeia

$$\frac{\partial z}{\partial r} = \frac{\partial f}{\partial r} (2r) + \frac{\partial f}{\partial y} st$$

$$\frac{\partial z}{\partial s} = \frac{\partial f}{\partial s} 2s + \frac{\partial f}{\partial y} rt$$

$$\frac{\partial z}{\partial t} = \frac{\partial f}{\partial t} (-1) + \frac{\partial f}{\partial y} rs$$

EXEMPLO

Considere F(r, \theta ) = f(x , y) onde x = r cos \theta e y = r sen \theta , sendo f(x,y) uma função diferenciável dada.

Observe que pela regra da cadeia $$ \frac{\partial F}{\partial r} (r, \theta ) = \frac{ \partial f }{\partial x}(x,y) \frac{\partial x}{\partial r} + \frac{ \partial f }{\partial y}(x,y) \frac{\partial y}{\partial r}$$ ou $$ \frac{\partial F}{\partial r} (r, \theta ) = cos \theta \frac{ \partial f }{\partial x}(x,y) + sen \theta \frac{ \partial f }{\partial y}(x,y)$$

Analogamente $$ \frac{\partial F}{\partial \theta } (r, \theta ) = \frac{ \partial f }{\partial x}(x,y) \frac{\partial x}{\partial \theta} + \frac{ \partial f }{\partial y}(x,y) \frac{\partial y}{\partial \theta }$$ ou $$ \frac{\partial F}{\partial \theta } (r, \theta ) = -r sen \theta \frac{ \partial f }{\partial x}(x,y) + r cos \theta \frac{ \partial f }{\partial y}(x,y)$$

Ou seja, $$ \frac{1}{r} \frac{\partial F}{\partial \theta } (r, \theta ) = – sen \theta \frac{ \partial f }{\partial x}(x,y) +  cos \theta \frac{ \partial f }{\partial y}(x,y)$$

Facilmente, conseguimos mostrar, usando produtos por seno e cosseno nas duas derivadas parciais de F(r, \theta ) , que

$$ \frac{\partial f}{\partial x} (x,y) = cos \theta \frac{\partial F}{\partial x} (r, \theta ) – \frac{ sen \theta}{r} \frac{\partial F}{\partial y} (r, \theta ) $$

$$ \frac{\partial f}{\partial y} (x,y) = \frac{cos \theta}{r}  \frac{\partial F}{\partial x} (r, \theta ) + sen \theta \frac{\partial F}{\partial y} (r, \theta ) $$

Lista de Exercícios:

• A Regra da Cadeia Para Campos Escalares | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• Derivadas Parciais de Segunda Ordem | Funções de Várias Variáveis
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Várias Variáveis Reais a Valores Reais ou Campos Escalares

Assista Nossa Vídeo-Aula Sobre A Regra da Cadeia: