Transformada de Laplace | Sistema Linear com Coeficientes Constantes

O método de Laplace pode ser aplicado para solucionar sistemas de Equações Diferenciais Ordinárias. Desde que sejam especificadas condições iniciais, a Transformada de Laplace reduz um sistema de equações diferenciais lineares com coeficientes constantes a um conjunto de equações algébricas simultâneas nas funções transformadas que pode ser resolvido matricialmente ou algebricamente.

Entendo o Método por Sistemas de E.D.O.’s de 1ª Ordem

Um sistema de equações lineares de primeira ordem com coeficientes constantes é dada da forma $$\left\{ \begin{array}{l} y_1′ = a_{11}y_1+a_{12}y_2 + g_1(t)\\ \\ y_2′ = a_{21}y_1+a_{22}y_2 + g_2(t) \end{array} \right. $$

Considerando Y_1 = \mathscr{L}(y_1), Y_2 = \mathscr{L}(y_2), G_1 = \mathscr{L}(g_1) e G_2 = \mathscr{L}(g_2), encontramos $$\left\{ \begin{array}{l}
sY_1 – y_1(0) = a_{11}Y_1+a_{12}Y_2 + G_1(s)
\\
sY_2 – y_2(0) = a_{21}Y_1+a_{22}Y_2 + G_2(s)
\end{array} \right.
$$ que fica $$\left\{ \begin{array}{l}
(a_{11} – s)Y_1 + a_{12}Y_2 = -y_1(0) + G_1(s)\\
\\
(a_{21})Y_1 + (a_{22} – s)Y_2 = -y_2(0) + G_2(s)
\end{array} \right.
$$ que pode ser escrito na forma matricial $$\left[ \begin{array}{lr}
a_{11} -s & a_{12}\\
\\
a_{21} & a_{22} – s\\
\end{array} \right] \left[ \begin{array}{l}
Y_1 \\
\\
Y_2
\end{array} \right] = \left[ \begin{array}{l}
G_1(s) -y_1(0) \\
\\
G_2(s) -y_2(0)
\end{array} \right],$$ donde $$ \left[ \begin{array}{l}
Y_1 \\
\\
Y_2
\end{array} \right] = \left[ \begin{array}{lr}
a_{11} -s & a_{12}\\
\\
a_{21} & a_{22} – s\\
\end{array} \right] ^{-1} \left[ \begin{array}{l}
G_1(s) -y_1(0) \\
\\
G_2(s) -y_2(0)
\end{array} \right]$$ que nos dá um sistema onde as soluções serão obtidas pela transforma inversa, sabendo que y_1(t) = \mathscr{L}^{-1} (Y_1) e y_2(t) = \mathscr{L}^{-1} (Y_2).

EXEMPLO 1: Resolva o problema de valor inicial $$\left\{ \begin{array}{rcl} x’ -2y & =  & 4t\\ \\ y’ +2y – 4x & =  & -4t-2 \end{array} \right. $$ cujas condições iniciais são dadas por x(0) = 4 e y(0) = -5.

Aplicando a transformada de Laplace nos dois lados das equações diferenciais, e considerando \mathscr{L}\{ x(t) \} = X(s) e \mathscr{L}\{ y(t) \} = Y(s) temos $$\left\{ \begin{array}{l} sX(s) – 2Y(s) = \frac{4s^2 + 4}{s^2}\\ \\ -4X(s) + (s+2) Y(s) = – \frac{5s^2 + 2s+ 4}{s^2} \end{array} \right. $$

Para eliminar Y(s) do sistema, multiplicamos a primeira equação por (s+2) e a segunda por 2 e depois somamos para obter $$\left[ s(s+2)-8 \right] X(s)= \frac{(s+2)(4s^2 +4)}{s^2}- \frac{10s^2 + 4s +8}{s^2}$$ que é simplificado para $$X(s) = \frac{4s-2}{(s+4)(s-2)}.$$

Para calcular a transformada inversa, escrevemos X(s) em termos de frações parciais $$X(s) = \frac{3}{s+4}+ \frac{1}{s-2}.$$ Logo, pela tabela de transformada de Laplace, descobrimos que $$x(t) = 3e^{-4t}+e^{2t}.$$

Para determinar y(t), poderíamos resolver o sistema para Y(s) e depois calcular sua transformada de Laplace inversa. Porém, é mais fácil apenas resolver a primeira equação no sistema para y(t) em termos de x(t) . Assim, $$y(t) = \frac{1}{2}x'(t)-2t.$$ Substituindo x(t) descobrimos que $$y(t) = -6e^{-4t}+e^{2t}-2t.$$

A solução do problema de valor inicial consiste no par de funções $$x(t) = 3e^{-4t}+e^{2t} \qquad \text{e} \qquad y(t) = -6e^{-4t}+e^{2t}-2t.$$

EXEMPLO 2: Considere uma mistura de água e sal em um tanque que gera as seguintes equações: $$\left\{ \begin{array}{l} y_1′ = 0,08y_1+0,02y_2 + 6\\ \\ y_2′ = 0,08y_1 – 0,08y_2
\end{array} \right. $$ cujas condições iniciais são dadas por y_1(0) = 0 e y_2(0) = 150.

Aplicando a transformada de Laplace obtemos $$\left\{ \begin{array}{l} (0,08 – s)Y_1 + 0,02Y_2 = \frac{6}{s}\\ \\ 0,08Y_1 + (-0,08 – s)Y_2 = -150 \end{array} \right. $$ o que nos leva à solução $$Y_1(s) = -\frac{1875\,s+30000}{625\,{s}^{3}+4950\,{s}^{2}-401\,s}$$ $$Y_2(s) = \frac{93750\,{s}^{2}-7500\,s-300}{625\,{s}^{3}+4950\,{s}^{2}-401\,s}$$ e aplicando a transformada de Laplace inversa, encontramos: $$y_1(t) = \frac{{e}^{-\frac{99\,t}{25}}\,\left( -\frac{1875046875\,\mathrm{senh}\left( \frac{\sqrt{10202}\,t}{25}\right) }{401\,\sqrt{10202}}-\frac{18750000\,\mathrm{cosh}\left( \frac{\sqrt{10202}\,t}{25}\right) }{401}\right) }{625}+\frac{30000}{401}$$ $$y_2 (t) = \frac{{e}^{-\frac{99\,t}{25}}\,\left( \frac{37406250\,\mathrm{cosh}\left( \frac{\sqrt{10202}\,t}{25}\right) }{401}-\frac{3815531250\,\mathrm{sinh}\left( \frac{\sqrt{10202}\,t}{25}\right) }{401\,\sqrt{10202}}\right) }{625}+\frac{300}{401}$$

De uma Equação Diferencial Ordinária para um Sistema de Equações

Suponhamos uma equação diferencial linear de ordem n dada inicialmente como $$ y^{(n)}= -\frac{a_0}{a_n}y – \frac{a_1}{a_n}y’ – \ldots – \frac{a_{n-1}}{a_n}y^{(n-1)} + f(t) .$$ Introduzindo as variáveis $$ y = x_1, \;\;\; y’ = x_2, \;\;\; \ldots, \;\;\; y^{(n-1)} = x_n , $$ decorre que  $$ y’ = x_1′ = x_2, \;\;\; y” = x_2′ = x_2, \;\;\; \ldots, \;\;\; y^{(n-1)} = x’_{n-1} =x_n  \;\;\; y^{(n)} = x’_{n}. $$

Logo, por estas relações podemos verificar que um equação diferencial linear de ordem n pode ser expressa como um sistema de equações de equações de primeira ordem com n equações: \begin{eqnarray} x’_1 & = & x_2 \\ x’_2 & = & x_3 \\ x’_3 & = & x_4 \\ & \vdots & \\ x’_{n-1} & = & x_n \\ x’_n & = & -\frac{a_0}{a_n}x_1 – \frac{a_1}{a_n}x_2 – \ldots – \frac{a_{n-1}}{a_n}x_{n} + f(t). \end{eqnarray}

EXEMPLO 3: Reduzindo a equação de terceira ordem $$2 y”’ – 6 y” +4y’ +y = \text{sen}(t) $$ a um sistema de equações de primeira ordem encontramos \begin{eqnarray} x’ _1 & = & x_2 \\ x’ _2 & = & x_3 \\ x’ _3 & = & -\frac{1}{2} x_1 – 2 x_2 +3 x_3 + \frac{1}{2} \text{sen}(t) \end{eqnarray} ao fazermos $$ y = x_1, y’ = x_2, y”’ = x_3 .$$

Que, após aplicar a Transformada de Laplace no sistema, considerando as condições iniciais $$x_1 (0) = A, \qquad x_2 (0) = B, \qquad x_3 (0) = C,$$ nos leva a  $$ \left[ \begin{array}{l} X_1 \\ X_2 \\ X_3 \end{array} \right] = \left[ \begin{array}{ccc} -s & 1 & 0\\ 0 &  – s & 0 \\ -1/2 & -2 & 3 -s \end{array} \right] ^{-1} \left[ \begin{array}{l} -A  \\ – B \\ \frac{1}{2(s^2 +1)} – C \end{array} \right]$$ $$ \left[ \begin{array}{l} X_1 \\ X_2 \\ X_3 \end{array} \right] = \left[ \begin{array}{ccc}-\frac{1}{s} & -\frac{1}{{s}^{2}} & 0\cr 0 & -\frac{1}{s} & 0\cr \frac{1}{2\,{s}^{2}-6\,s} & \frac{4\,s+1}{2\,{s}^{3}-6\,{s}^{2}} & -\frac{1}{s-3}\end{array} \right] \left[ \begin{array}{l} -A  \\ – B \\ \frac{1}{2(s^2 +1)} – C \end{array} \right].$$

Efetuando a multiplicação de matrizes, encontramos \begin{eqnarray} X_1 (s) & = & \frac{A}{s} + \frac{B}{{s}^{2}} \\ X_2 (s) & = & \frac{B}{s} \\ X_3 (s) & = & \frac{-A}{2\,{s}^{2}-6\,s} -B \times \frac{4\,s+1}{2\,{s}^{3}-6\,{s}^{2}} – \frac{1}{s-3} \left( \frac{1}{2(s^2 +1)} – C \right)\\ & = & \frac{-A}{2\,{s}^{2}-6\,s} -B \times \frac{4\,s+1}{2\,{s}^{3}-6\,{s}^{2}} + \frac{\left( 2\,{s}^{2}+2\right) \,C-1}{2\,{s}^{3}-6\,{s}^{2}+2\,s-6} \end{eqnarray} e aplicando a Transformada de Laplace Inversa obtemos \begin{eqnarray} x_1 (t) & = & A + B \\ x_2 (t) & = & B \\ x_3 (t) &= & -A \left( \frac{{e}^{3\,t}}{6}-\frac{1}{6} \right) – B \left( \frac{13\,{e}^{3\,t}}{18}-\frac{t}{6}-\frac{13}{18} \right) + \\ & & + \frac{{e}^{3\,t}\,\left( 20\,C-1\right) }{20}+\frac{3\,\mathrm{sen}\left( t\right) }{20}+\frac{\mathrm{cos}\left( t\right) }{20} \end{eqnarray}

Aplicações dos Sistemas de Equações Diferenciais por Transformada de Laplace

Agora, vamos falar sobre algumas aplicações elementares que envolvem sistemas de equações diferenciais. As soluções dos problemas que vamos considerar podem ser obtidas, seja pelos método da seção precedente seja pela aplicação da transformada de Laplace.

MOLAS ACOPLADAS

Duas massas m_1 e m_2 estão apenas a duas molas A e B de massa desprezível, com contantes k_1 e k_2 , respectivamente. Por sua vez, as duas molas estão unidas conforme mostra a figura abaixo:

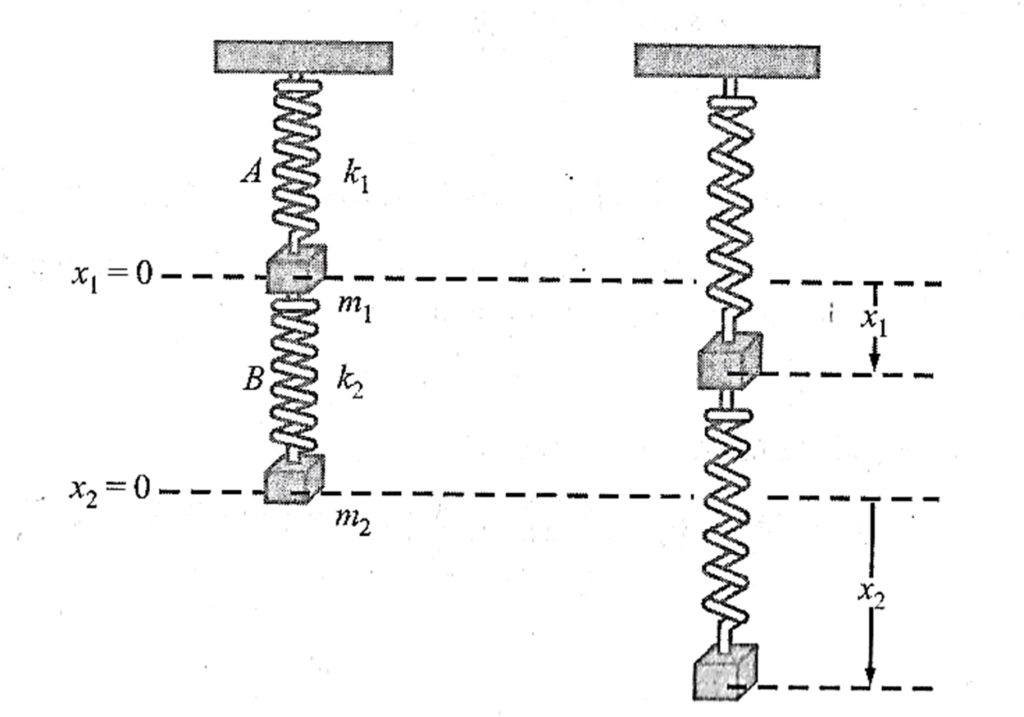
Denotemos por x_1(t) e x_2(t) são deslocamentos verticais das massas em relação às duas posições de equilíbrio. Quando o sistema está em movimento, a mola B está sujeita tanto a um alongamento como a uma compressão; logo, seu alongamento toral é x_2 - x_1 . Decorre, portanto, da lei de Hooke, que as molas A e B exercem forças $$ -k_1 x_1 \text{ e } k_2 \left( x_2 – x_1 \right),$$ respectivamente, sobre m_1 .

Se nenhuma força externa atua sobre o sistema e se não existe qualquer força de amortecimento, então a força resultante sobre m_1 é $$-k_1 x_1 + k_2 \left( x_2 – x_1 \right).$$ Pela segunda lei de Newton, podemos escrever $$ m_1 \frac{d^2 x_1}{dt^2} = -k_1 x_1 + k_2 \left( x_2 – x_1 \right).$$

Analogamente, a força externa resultante sobre a massa m_2 é devida somente ao alongamento total de B; isto é, $$-k_2 \left( x_2 – x_1 \right),$$  decorrendo, assim, que $$ m_2 \frac{d^2 x_2}{dt^2} = -k_2 \left( x_2 – x_1 \right).$$

Em outras palavras, o movimento do sistema acoplado é representado pelo sistema de equações diferenciais de segunda ordem simultâneas \begin{eqnarray} m_1 x_{1} ”& = & -k_1 x_1 + k_2 \left( x_2 – x_1 \right)\\ \\ m_2 x_{2}” & =  &-k_2 \left( x_2 – x_1 \right) \end{eqnarray} e este sistema pode ser resolvido usando a Transformada de Laplace.

REDES ELÉTRICAS

Uma rede elétrica com mais de uma malha também dá origem a equações diferenciais simultâneas. Conforme vemos na ilustração abaixo, a corrente i_1 (t) se bifurca nas direções indicadas no ponto B_1 , chamado ponto de ramificação da rede. 

Pela primeira lei de Kirchhoff, podemos escrever $$ i_1 (t) = i_2 (t) + i_3 (t). \tag{1}$$ Além disso, podemo também aplicar a segunda lei de Kirchhoff a cada malha. Para a malha A_1 B_1 B_2 A_2 A_1 , somando as quedas de voltagem através de cada parte da malha, obtemos $$E(t) = i_1 R_1 + L_1 \frac{d i_2 }{dt}+ i_2 R_2.$$ Analogamente, para a malha A_1 B_1 C_1 C_2 A_2 A_1 , temos $$ E(t) = i_1 R_1 + L_2 \frac{d i_3 }{dt}.$$ Utilizando (1) para eliminar i_1 nas duas equações diferenciais, obtemos um sistema de equações diferenciais de primeira ordem para as correntes i_2 (t) e i_3 (t) \begin{eqnarray} L_1 \frac{d i_2 }{dt} + (r_1 + R_2) i_2 + R_1 i_3 & = & E(t) \\ L_2 \frac{d i_3 }{dt} + R_1  i_2 + R_1 i_3 & = & E(t) \end{eqnarray}, onde dadas as condições iniciais adequadas podemos usar a Transformada de Laplace para solucionar.

Usando um raciocínio análogo, podemos mostrar que o sistema de equações diferenciais que descrevem as correntes i_1 (t) e i_2 (t) na rede que contém um resistor, um indutor e um capacitor conforme a figura abaixo,

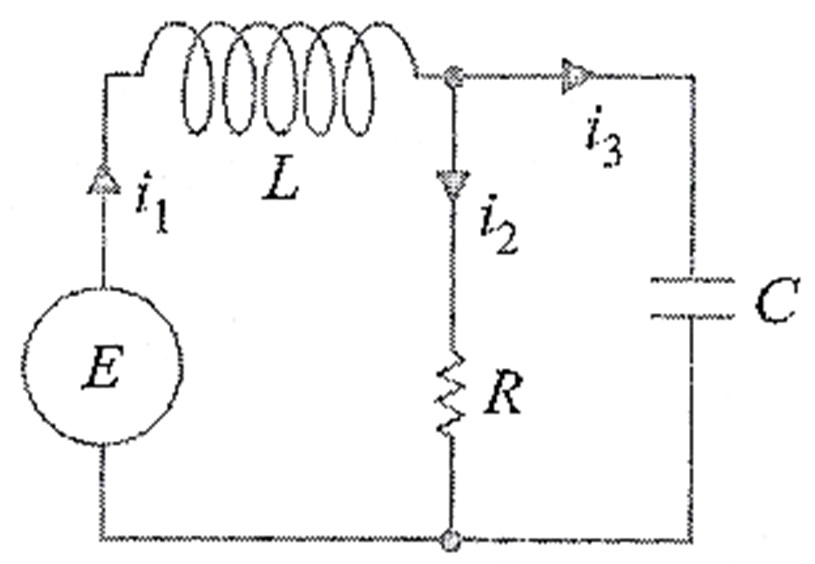
é \begin{eqnarray} L \frac{d i_1 }{dt} + R i_2 + R_1 i_3 & = & E(t) \\ RC \frac{d i_2 }{dt} +  i_2 – i_1 & = & 0 \end{eqnarray}.

Referências Blibliográficas

1. BOYCE, W.; DIPRIMA R. Equações Diferenciais Elementares e Problemas de Valores de Contorno, LTC, Rio de Janeiro,2002
2. ZILL, D. G. Equações Diferenciais com Aplicações em Modelagem, Editora Pioneira – Thomson Learning, São Paulo, 2003.
3. KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.

Leia Mais:

• Circuitos em Série | Aplicações da Transformada de Laplace
• Solucionando Eq. Diferenciais Ordinárias Via Transformada de Laplace
• Transformada de Laplace Inversa | Lista de Exercícios Resolvidos
• Transformada de Laplace | Das Definições Básicas à Função Delta