A matemática financeira estuda o valor do dinheiro ao longo do tempo. Para isso precisamos entender conceitos básicos como o fluxo de caixa a taxa de juros.

O objeto essencial do estudo da matemática financeira são os juros, que podem ser entendidos como sendo a remuneração do capital empregado. Para entender como o dinheiro sofre a ação do tempo geralmente usa-se o fluxo de caixa.
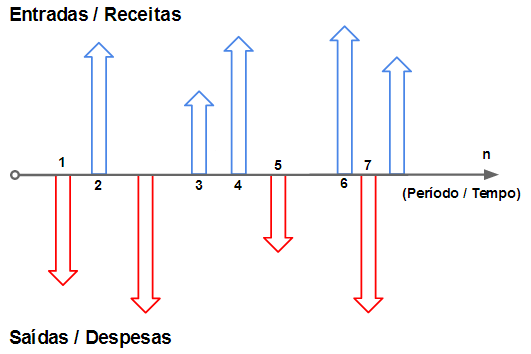 Diagrama de fluxo de caixa: A linha horizontal registra a escala de tempo, e as setas indicam saídas (para baixo) ou aplicações (para cima) de dinheiro.
Diagrama de fluxo de caixa: A linha horizontal registra a escala de tempo, e as setas indicam saídas (para baixo) ou aplicações (para cima) de dinheiro.
Isso porque essencialmente receber uma quantia em dinheiro hoje ou no futuro não é a mesma coisa. Efetuar análises e comparações dos vários fluxos de entrada e saída de dinheiro de caixa verificados em diferentes momentos é o objetivo.
Protelarmos uma entrada de recursos (caixa) nos atribui um certo sacrifício financeiro. Esse sacrifício têm um custo, o qual denominamos de “juros”. Os juros são calculados através de uma taxa. As taxas de juros são sempre expressas em percentual e em unidade de tempo.
1 – Taxas de Juros
O que são taxas de juros?
taxa percentual taxa unitária.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Taxas de juros percentual e unitária
taxa de juro percentualtaxa unitária
| EXEMPLOS DE TAXAS DE JUROS PERCENTUAIS E UNITÁRIAS | |
| Taxa Percentual | Taxa Unitária |
| 1,5% | 0,015 |
| 8% | 0,08 |
| 17% | 0,17 |
| 86% | 0,86 |
| 120% | 1,20 |
| 1.500% | 15,0 |
Taxas de Juros e Prazos
Pra que servem as taxas de juros?
As taxas de juros devem ser eficientes de maneira a remunerar:
- O risco envolvido na operação (empréstimo ou aplicação), representado genericamente pela incerteza com relação ao futuro;
- a perda do poder de compra do capital motivada pela inflação. A inflação é um fenômeno que corrói o capital, determinando um volume cada vez menor de compra com o mesmo montante;
- o capital emprestado/aplicado. Os juros devem gerar um lucro (ou ganho) ao proprietário do capital como forma de compensar sua privação por determinado período de tempo. Este ganho é estabelecido basicamente em função das diversas outras oportunidades de investimentos e definido por custo de oportunidade.
Leia Mais:
- Juros Simples | Fórmulas de Exercícios Resolvidos
- Manual Básico da Calculadora HP 12C | Matemática Financeira
- Calculadora HP 12c | Como calcular Juros Simples e a Taxa?
- Calculadora HP 12c | Operações algébricas, datas e porcentagem
Referências Bibliográficas do Artigo:
- Fábio Gomes de Faria – “Matemática Financeira – Prática e Fácil” [Link do livro]
- Alexandre Assaf Neto – “Matemática Financeira e suas Aplicações” [Link do livro]

