Sistemas Lineares: 5 Exercícios Resolvidos Passo-a-Passo

Precisa de ajuda para resolver sistemas lineares? Confira estes 5 exercícios resolvidos que irão guiá-lo durante o processo e melhorar sua compreensão dos sistemas de equações lineares.

Se você está estudando sistemas lineares, neste artigo, fornecemos soluções para 5 exercícios diferentes que o ajudarão a compreender o conceito dos sistemas de equações lineares e a melhorar suas habilidades de resolução de problemas. Quer você seja um iniciante ou um aluno de graduação, estes exercícios resolvidos irão guiá-lo passo a passo pelo processo.

O que São Sistemas Lineares?

Sistemas lineares são conjuntos de equações lineares que possuem uma ou mais incógnitas. Essas equações são chamadas de lineares porque envolvem apenas variáveis elevadas à primeira potência e não possuem termos com expoentes diferentes ou produtos entre as variáveis.

Resolver um sistema linear significa encontrar os valores das incógnitas que satisfaçam todas as equações simultaneamente

Como Classificar Sistemas Lineares Quanto a Solução?

Existem três classificações possíveis para sistemas lineares quanto à solução: sistema possível e determinado, sistema possível e indeterminado e sistema impossível.

1. Sistema possível e determinado: Nesse caso, o sistema possui uma única solução.

2. Sistema possível e indeterminado: Nesse caso, o sistema possui infinitas soluções.

3. Sistema impossível: Nesse caso, o sistema não possui solução.

Ao classificar um sistema linear, é importante analisar as equações e determinar se elas são consistentes ou inconsistentes. Isso ajudará a identificar o tipo de solução que o sistema possui. Praticar a classificação de sistemas lineares é fundamental para aprofundar seu conhecimento em álgebra linear e resolver problemas mais complexos.

Por que estudar Sistemas Lineares?

Estudar sistemas lineares é fundamental para a compreensão e resolução de problemas matemáticos mais complexos. Os sistemas lineares são amplamente utilizados em diversas áreas, como engenharia, física, economia e ciências da computação.

Além disso, o estudo de sistemas lineares ajuda a desenvolver habilidades de análise, raciocínio lógico e resolução de problemas, que são essenciais em diversas áreas profissionais. Portanto, dedicar tempo ao estudo e prática de sistemas lineares é uma maneira eficaz de aprimorar suas habilidades matemáticas e ampliar suas oportunidades acadêmicas e profissionais.

5 Melhores Livros Para Estudar Sistemas Lineares

1. “Fundamentos de matemática elementar – Volume 4: Sequências, matrizes, determiantes e sistemas”, de Gelson Iezzi.
2. “Álgebra Linear”, de Alfredo Steinbruch
3. “Álgebra Linear”, de J. L. Boldrini e outros
4. “Matrizes e Sistemas de Equações Lineares”, de Nilo Kuhlkamp
5. “Álgebra linear e suas aplicações”, de Gilbert Strang

5 Exercícios Resolvidos Sobre Sistemas Lineares

1) Resolva os sistemas lineares abaixo usando a técnica mais adequada:

a) \left\{ \begin{array}{lll} 2x-3y & = & 1\\ x+2y & = & 4 \end{array} \right. 

Solução: Da primeira equção temos que $$y = \frac{2x-1}{3}.$$ E substituindo na segunda equação temos $$ x + 2 \left( \frac{2x-1}{3} \right) = 4 \Rightarrow x + \frac{4x-2}{3} = 4 \Rightarrow 3x + 4x – 2 = 12 \Rightarrow x = 2.$$ Assim, $$y = \frac{2\times 2 -1}{3} = 1.$$ Portanto o conjunto solução deste sistema é \{ 2,1 \} .

b) \left\{ \begin{array}{lll} x - 2 y  & = & 4\\ -2x +4y & = & -8 \end{array} \right. 

Solução: Observe que a segunda equação deste sistema é múltipla da primeira equação, logo, usando o método da adição, encontramos: $$ \left\{ \begin{array}{lll} x – 2 y  & = & 4\\ -2x +4y & = & -8 \end{array} \right.  \sim \left\{ \begin{array}{rll} x – 2 y  & = & 4\\ 0 & = & 0 \end{array} \right. $$ Por isso o sistema é possível e indeterminado e usando a primeira equação do sistema temos que $$ x – 2y = 4 \Rightarrow x = 2y +4.$$ Portanto o conjunto solução deste sistema é \{ (2y+4, y); y \in \mathbb{R} \} .

c) \left\{ \begin{array}{lll} 3x - y & = & 2\\6x - 2y  & = & 3\end{array} \right. 

Solução: Multiplicando a primeira equação por -2 e somando na segunda equação encontramos $$ \left\{ \begin{array}{lll} 3x – y & = & 2\\6x – 2y  & = & 3\end{array} \right. \sim \left\{ \begin{array}{rll} 3x – y & = & 2\\ 0  & = & -1 \end{array} \right.$$ Portanto o sistema é impossível.

2) Determine o valor de m \in \mathbb{R} para que o sistema linear abaixo seja possível e determinado: $$ \left\{ \begin{array}{lll} x+2y+z  & = & 5\\ 2x-y+2z & = & 5 \\ 3x+y+mz & = & 0 \end{array} \right. $$

Solução: Para que este sistema seja possível e determinado precisamos que o determinante $$ \left| \begin{array}{rrrr} 8 & -4 & 1\\ 3 & 7 & 9 \\  -4 & 2 & 5\\ \end{array} \right| = -m +12 +2 +3 -2 -4m = -5m +15 $$ seja diferente de zero. Assim $$ -5m +15 \neq 0 \Rightarrow m \neq 3 .$$ Portanto, os valores de m \in \mathbb{R} , para que o sistema seja possível e determinado, são dados pelos elementos do conjunto: $$ \{ m \in \mathbb{R}; m \neq 3 \} .$$

3) Escalone e resolva os sistemas lineares abaixo:

a) \left\{ \begin{array}{lll} 3x+2y+z & = & 10\\ x+2y +2z & = & 11 \\ x+y +z & = & 6 \end{array} \right. 

Solução: Escalonando o sistema linear acima obtemos

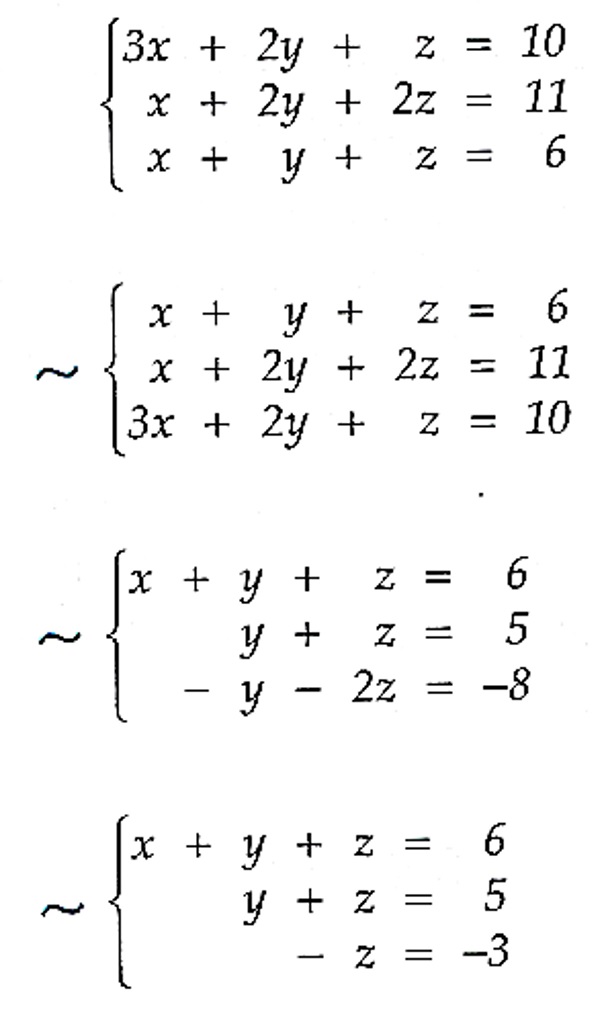
Daí, temos que z = 3 . Substituindo este valor na segunda equação, temos que $$ y + 3 = 5 \Rightarrow y = 2. $$ Agora, substituindo estes dois valores na primeira equação obtemos $$ x + y + z = 6 \Rightarrow x + 2 + 3 = 6 \Rightarrow x = 1 .$$ Portanto, teremos S = \{ 1,2,3 \} .

b) \left\{ \begin{array}{lll}a + b + c  & = & 12\\ 3a - b +2c & = & 14 \\ 2a - 2b +c & = & -3 \end{array} \right. 

Solução: Escalonando este sistema encontramos

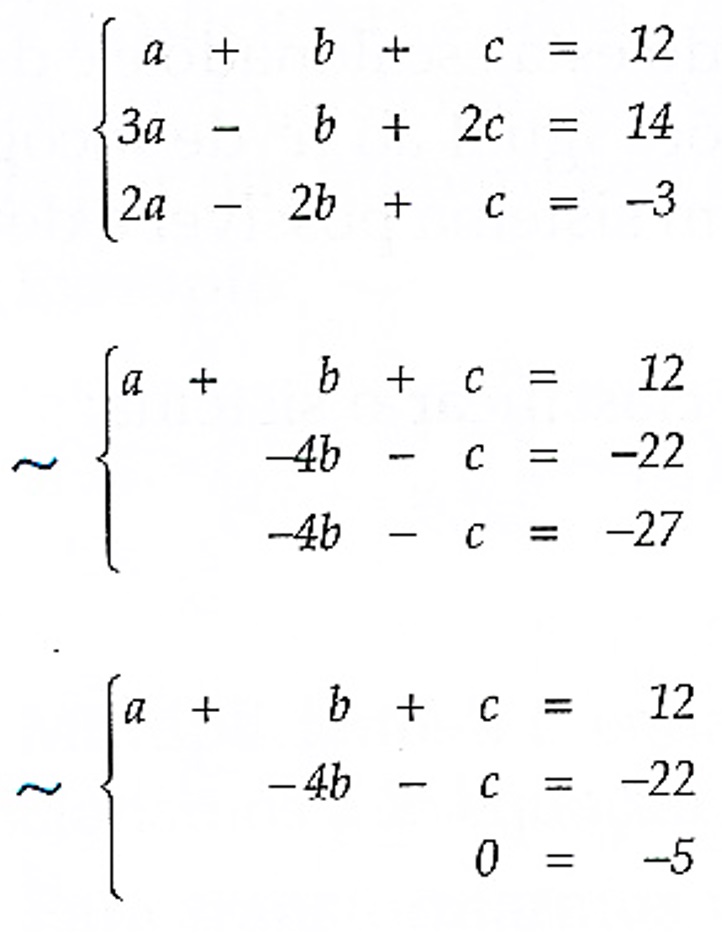
Portanto, o sistema é impossível, pois a 3ª equação nunca será satisfeita. Assim, S = \emptyset .

c) \left\{ \begin{array}{lll} x+2y-z& = & 4\\3x - y  + z & = & 5\end{array} \right. 

Solução: Escalonando este sistema linear obtemos

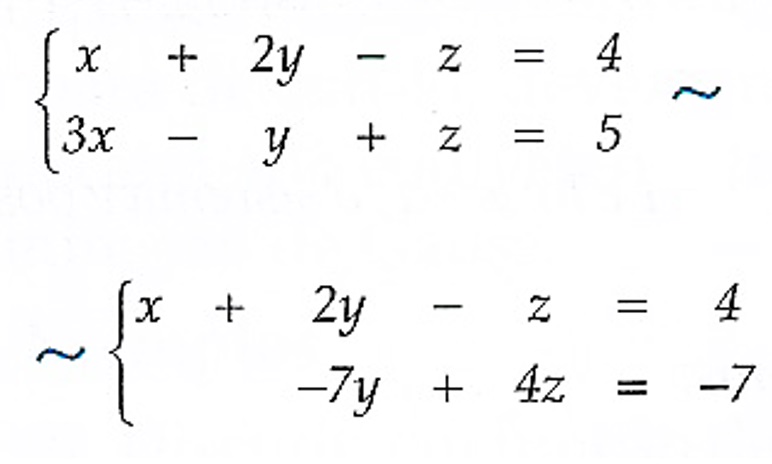
Desta forma, o sistema é possível e indeterminado, sendo y a variável a ser isolada na segunda equação. Assim, $$ -7y + 4z = -7 \Rightarrow y = \frac{4z+7}{7} .$$ Substituindo na primeira equação: $$ x + 2 \left( \frac{4z+7}{7} \right) – z = 4 \Rightarrow x = \frac{14-z}{7}.$$ Portanto, $$ S = \left\{ \frac{14-z}{7} , \frac{4z+7}{7} , z ; z \in \mathbb{R} \right\} .$$

4) Resolva o sistema linear abaixo usando a Regra de Cramer: $$ \left\{ \begin{array}{lll} x+2y+3z  & = & 2\\ 2x-y+ z & = & -1 \\ -2x-3y+3z & = & -11 \end{array} \right. $$

Solução: Vamos calcular os determinantes que iremos usar na Regra de Cramer: $$ \text{det}(A) =  \left| \begin{array}{rrrr} 1 & 2 & -2 \\ 2 & -1 & -3 \\  3 & 1 & 3\\ \end{array} \right| = -40 \qquad  \text{det}( D_1 ) = \left| \begin{array}{rrrr} 2 & 2 & -2 \\ -1 & -1 & -3 \\  -11 & 1 & 3\\ \end{array} \right| = -40 \\  \text{det}( D_2 ) = \left| \begin{array}{rrrr} 1 & 2 & -2 \\ 2 & -1 & -3 \\  3 & – 11 & 3 \\ \end{array} \right| = – 80 \qquad \text{det}(D_3) =  \left| \begin{array}{rrrr} 1 & 2 & 2 \\ 2 & -1 & -1 \\  3 & 1 & -11\\ \end{array} \right| = 40.$$ Desta forma, temos que $$ x = \frac{\text{det}( D_1 )}{\text{det}(A )} = 1; \qquad y = \frac{\text{det}( D_2 )}{\text{det}(A )} = 2 ; \qquad z = \frac{\text{det}( D_3 )}{\text{det}(A )} = -1.$$ Portanto, pela Regra de Cramer, a solução do sistema é S = \{(1,2,-1) \} .

5) Considere o sistema $$ \left\{ \begin{array}{lll} x \cdot \text{sen} ( \theta ) \; – \; y \cdot \text{cos} ( \theta ) & = &  \text{sen} ( \beta ) \\ x \cdot \text{cos} ( \theta ) + y \cdot \text{sen} ( \theta )& = &  \text{cos} ( \theta ) \end{array} \right. $$

a) Mostre que, qualquer que seja \theta \in \mathbb{R} , o sistema linear é possível e determinado;

Solução: Calculemos $$ D = \left| \begin{array}{rrr} \text{sen} ( \theta ) & – \text{cos} ( \theta ) \\ \text{cos} ( \theta ) & \text{sen} ( \theta )\\ \end{array} \right| = \text{sen} ^2 ( \theta ) + \text{cos}^2 ( \theta ) = 1,$$ pela relação fundamental trigonométrica. Como D \neq , concluímos que, para todo \theta \in \mathbb{R} , o sistema é sempre possível e determinado.

b) Resolva este sistema linear pela  Regra de Cramer.

Solução: Observe que $$ D_1 = \left| \begin{array}{rrr} \text{sen} ( \beta ) & – \text{cos} ( \theta ) \\ \text{cos} ( \beta ) & \text{sen} ( \theta )\\ \end{array} \right| = \text{sen} ( \beta ) \text{sen} ( \theta ) + \text{cos} ( \beta ) \text{cos} ( \theta ) = \text{cos} ( \theta – \beta ) $$ $$ D_2 = \left| \begin{array}{rrr} \text{sen} ( \theta ) & \text{sen} ( \beta ) \\ \text{cos} ( \theta ) & \text{cos} ( \beta ) \\ \end{array} \right| = \text{cos} ( \beta ) \text{sen} ( \theta ) – \text{sen} ( \beta ) \text{cos} ( \theta ) = \text{sen} ( \theta – \beta ). $$ Aplicando a Regra de Cramer, temos que $$ x = \frac{D_1}{D} = \frac{\text{cos} ( \theta – \beta )}{1} = \text{cos} ( \theta – \beta ) $$ e $$ y = x = \frac{D_2}{D} = \frac{\text{sen} ( \theta – \beta )}{1} = \text{sen} ( \theta – \beta ) $$ são as soluções deste sistema linear.

5 Melhores Livros Para Estudar Sistemas Lineares

1. “Fundamentos de matemática elementar – Volume 4: Sequências, matrizes, determiantes e sistemas”, de Gelson Iezzi.
2. “Álgebra Linear”, de Alfredo Steinbruch
3. “Álgebra Linear”, de J. L. Boldrini e outros
4. “Matrizes e Sistemas de Equações Lineares”, de Nilo Kuhlkamp
5. “Álgebra linear e suas aplicações”, de Gilbert Strang

Leia Mais:

1. Sistemas Lineares de Ordem 2: Métodos da Adição e da Substituição
2. Sistemas Lineares: Forma Matricial e a Regra de Cramer
3. Eliminação Gaussiana: Resolvendo sistemas lineares por escalonamento
4. Sistemas Lineares | Lista de Exercícios Resolvidos
5. Matrizes e Sistemas Lineares | 1ª Lista de Exercícios Resolvidos