Máximos e Mínimos de Campos Escalares | 2ª Lista de Exercícios Resolvidos

Diz-se que (x_0, y_0) é ponto de máximo de uma função f(x,y) se $$f(x,y) \leq f(x_0, y_0)$$ para todo (x,y) \in D_f. Analogamente, (x_0, y_0) é ponto de mínimo de uma função f(x,y) se $$f(x,y) \geq f(x_0, y_0)$$ para todo (x,y) \in D_f.

Seja (x_0, y_0) um ponto interior de D_f e suponhamos que \frac{\partial f}{\partial x}(x_0,y_0) e \frac{\partial f}{\partial y}(x_0,y_0) existam. Nestas condições, uma condiçao necessária para que (x_0, y_0) seja um extremante local de f é que \frac{\partial f}{\partial x}(x_0,y_0) = \frac{\partial f}{\partial y}(x_0,y_0) = 0.

Agora, seja f duas vezes diferenciável e seja (x_0, y_0) um ponto interior do domínio de f. Então:

1. Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) > 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de mínimo local de f
2. Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) < 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de máximo local de f
3. Se H(x_0,y_0) < 0, então (x_0,y_0) não será um extremante local, neste caso será um ponto de sela de f.
4. Se H(x_0,y_0) = 0 nada podemos afirmar quanto ao ponto (x_0,y_0)

Além disso, se f(x,y) for contínua num conjunto compacto então esta função assumirá um valor de máximo e de mínimo neste conjunto.

2ª Lista de Exercícios Resolvidos sobre Máximos e Mínimos

1. Determine os valores máximo e mínimo da função dada, na região indicada.

a) f(x,y) = x+ 2y; no retângulo de vértices (1,-2), (1,2), (-1,2) e (-1,-2).

Como \nabla f(x,y) = (1,2) então não existem pontos críticos a serem determinados dentro do retângulo abaixo:

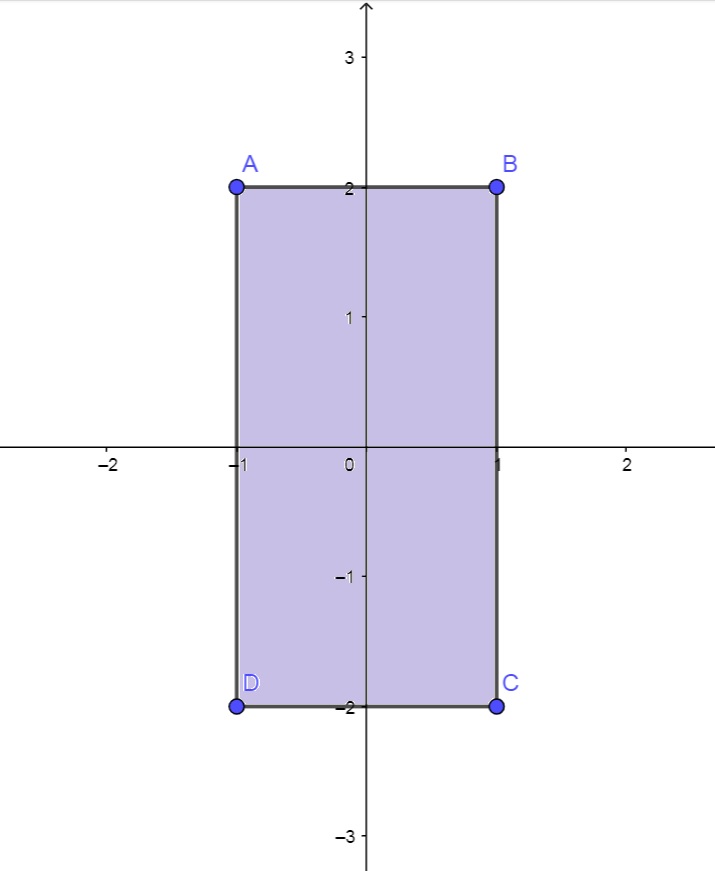
Vamos analisar o que acontece nos pontos de fronteira. Observe que no segmento \bar{AB} temos pontos na forma (x,2). Desta forma, $$g(x) = f(x,2) = x+4$$ é uma função que não admite pontos críticos dentro das técnicas do cálculo de uma variável real.

De modo análogo chegaremos à mesma conclusão para os demais três segmentos. Ou seja, os únicos pontos candidatos a máximo e mínimo dentro do retângulo são os vértices.

Como $$f(-1,2) = 3;\;\;\; f(1,2) = 5; \;\;\;f(-1,-2) = -5; \;\;\;e\;\;\; f(1,-2) = -3$$ podemos concluir que (1,2) é ponto de máximo e (-1,-2) é ponto de mínimo dentro do retângulo.

b) z= xy; no círculo x^2 + y^2 \leq 1.

Observando que $$ \nabla f(x,y) = (y,x) = (0,0) \Leftrightarrow (x,y) = (0,0),$$ percebemos que temos apenas um candidato a extremante local dentro do círculo x^2 + y^2 < 1.

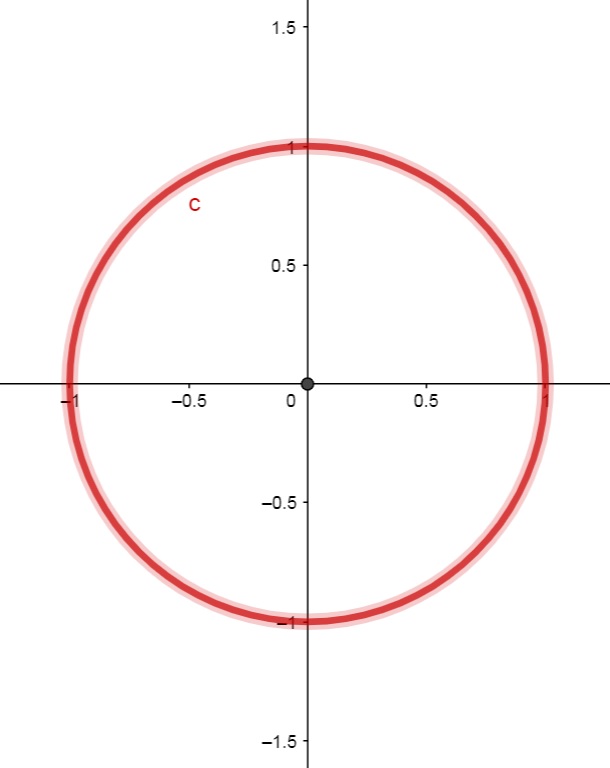Como H(x,y) = -1, então esse ponto (x,y) = (0,0) é um ponto de sela de f(x,y) .

Agora precisamos investigar o que acontece na fronteira do círculo x^2 +y^2 = 1.

Para isso, considere $$x(t) = cost \;\;\;e \;\;\; y = sen(t).$$ Logo, os valores de f(x,y) na fronteira do círculo é dada por $$g(t) = f(cost, sent) = cos(t) sen(t) = \frac{1}{2} sen(2t)\;\;\;0\leq t \leq 2 \pi.$$

Usando técnicas de investigação de extremantes de funções de uma variável, podemos encontrar t = \frac{1}{4} \pi e t = \frac{5}{4} \pi como pontos de máximo; e t = \frac{3}{4} \pi e t = \frac{7}{4} \pi como pontos de mínimo.

Isso pode ser visto também pelo gráfico abaixo:

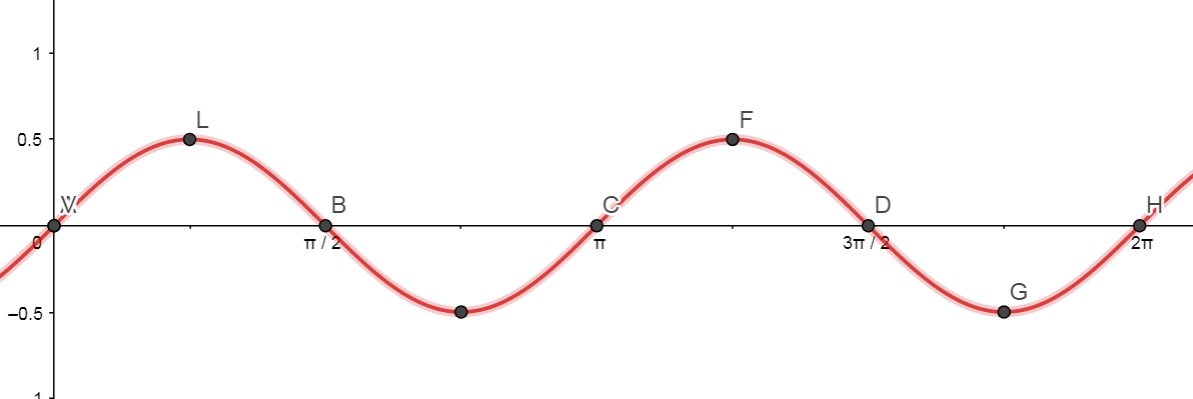
Daí, segue que $$\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\;\;\;e\;\;\; \left( -\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \right),$$ ambos os pontos com imagem de f igual \frac{1}{2} , são pontos de máximo de f(x,y).

Analogamente, podemos verificar que $$\left( \frac{\sqrt{2}}{2}, – \frac{\sqrt{2}}{2} \right)\;\;\;e\;\;\; \left( -\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2} \right),$$ ambos os pontos com imagem de f igual - \frac{1}{2} , são pontos de mínimo de f(x,y).

2) Determine os extremantes da função f(x,y) = xy(3 - x - y) , definida no domínio A = \{ (x,y) \in \mathbb{R} ^2 | x \geq 0, y \geq 0, x+y \leq 3 \} .

SOLUÇÃO: O conjunto A está ilustrado abaixo:

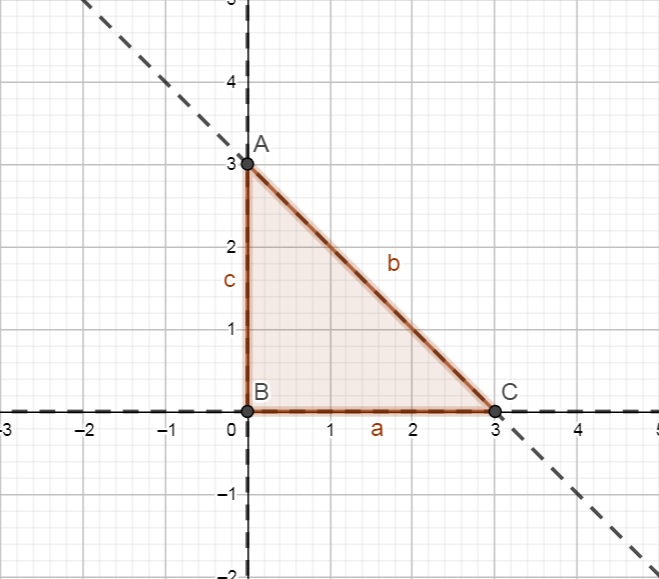
Esta função tem um único ponto crítico no interior conjunto A, os restantes estão todos na fronteira. Eles são obtidos resolvendo as equações $$ \frac{\partial f}{\partial x} = 3y – 2xy – y^2 = 0$$ $$ \frac{\partial f}{\partial y} = 3x – 2xy – x^2 = 0$$ o que nos dão os pontos $$(0,0), \;\;\; (3,0), \;\;\; (1,1), \;\;\;e\;\;\; (0,3).$$

O único interior ao conjunto A é o ponto (1,1).

Porém, observe que todos os pontos da fronteira anulam a função. Isso facilmente pode ser visto na imagem abaixo, com o gráfico da função tomando o domínio restrito ao conjunto A:

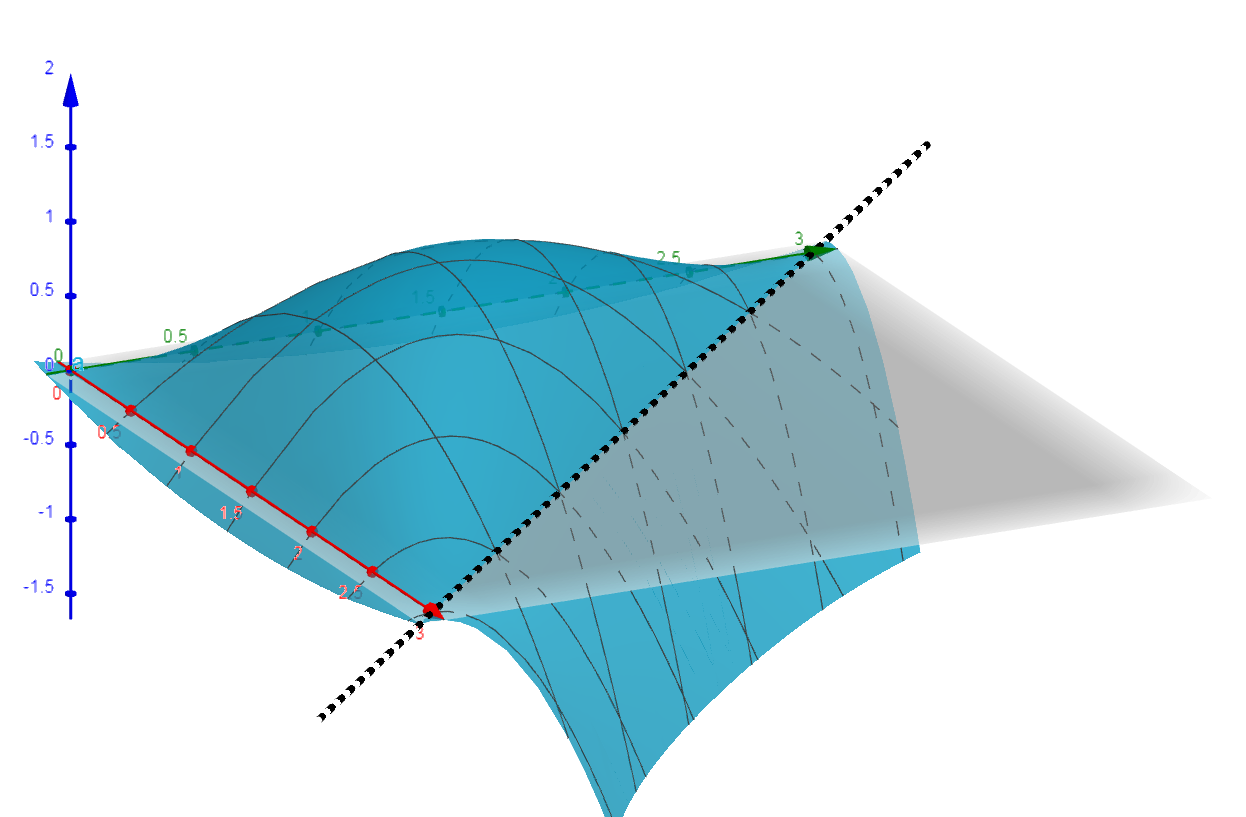
Como todo os demais pontos além de (1,1), estão sobre a fronteira e a função se anula nos pontos da fronteira, podemos concluir, percebendo que f(1,1)=1, que este é obviamente um ponto de máximo da função dentro deste conjunto.

Não havendo outro ponto crítico interno ao conjunto A, só podemos assumir que os pontos de mínimo da função, com domínio restrito ao conjunto A, estão nos pontos de fronteira, cujas imagens são sempre zero.

3) Determine os extremantes da função f(x,y) =(x-2)^2 y + y^2 - y , definida no domínio A = \{ (x,y) \in \mathbb{R} ^2 | x \geq 0, y \geq 0, x+y \leq 4 \} .

SOLUÇÃO: Primeiro procuramos localizar os pontos críticos da função ao resolver o sistema $$ \frac{\partial f}{\partial x} = 2y(x-2) = 0$$ $$ \frac{\partial f}{\partial y} =(x-2)^2 +2y -1 = 0$$

Das soluções encontradas, (1,0), (3,0) e (2, 1/2), só iremos considerar a última, pois ela é a única interna ao conjunto A. Como $$ H(2,1/2) = -2 <0 $$ $$ \frac{\partial^2 f}{\partial x^2} (2,1/2)> 0$$ podemos ver que este ponto é um mínimo relativo.

Devemos agora analisar o comportamento da função na fronteira de A, um triângulo que tem como vértices os ponto do plano: O(0,0), A(4,0) e B(0,4).

No segmento OA (y=0 e 0 \leq x \leq 4 ) a função é sempre nula, de forma que todos os pontos de OA são de máximo e mínimo para a função f(x,0).

No segmento OB (x=0 e 0 \leq y \leq 4 ) a função f(x,y) se reduz a h(y) = y^2 +3y. Como esta função é estritamente crescente, ela tem um mínimo em y = 0 e uma máximo em y=4.

Finalmente, no segmento AB (x= 4-y) a função se reduz a $$F(y) = f(4-y, y) = y^3 – 3y^2 +3y; 0 \leq y \leq 4 .$$ Esta função é crescente neste intervalo com valor mínimo no ponto y=0 (que é o ponto A) e máximo no ponto y=4 (que é o ponto B).

Portanto, verificando as imagens destes casos destacados sobre a fronteira de A: f(x,y) assume o valor mínimo em todos os pontos  do segmento OA e o valor máximo no ponto B(0,4).

Comparando os valores de f(x,y) em OA, B e (1,1), elas são zero, 28 e -1/4, respectivamente. Portanto, podemos concluir que que esta função assume valor mínimo igual a -1/4 no ponto (1,1) e valor máximo, igual a 28, no ponto (0,4), sobre a fronteira.

Leia Mais:

• Máximos e Mínimos de Funções de Várias Variáveis
• Máximos e Mínimos de Campos Escalares | 1ª Lista de Exercícios Resolvidos
• Máximos e Mínimos de Campos Escalares | 3ª Lista de Exercícios Resolvidos
• Maximos e Mínimos: O Método dos Multiplicadores de Lagrange

Assista Nossa Vídeo-Aula Sobre Máximos e Mínimos: