Máximos e Mínimos de Campos Escalares | 3ª Lista de Exercícios Resolvidos

Diz-se que (x_0, y_0) é ponto de máximo de uma função f(x,y) se $$f(x,y) \leq f(x_0, y_0)$$ para todo (x,y) \in D_f. Analogamente, (x_0, y_0) é ponto de mínimo de uma função f(x,y) se $$f(x,y) \geq f(x_0, y_0)$$ para todo (x,y) \in D_f.

Seja (x_0, y_0) um ponto interior de D_f e suponhamos que \frac{\partial f}{\partial x}(x_0,y_0) e \frac{\partial f}{\partial y}(x_0,y_0) existam. Nestas condições, uma condiçao necessária para que (x_0, y_0) seja um extremante local de f é que \frac{\partial f}{\partial x}(x_0,y_0) = \frac{\partial f}{\partial y}(x_0,y_0) = 0.

Agora, seja f duas vezes diferenciável e seja (x_0, y_0) um ponto interior do domínio de f. Então:

1. Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) > 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de mínimo local de f
2. Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) < 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de máximo local de f
3. Se H(x_0,y_0) < 0, então (x_0,y_0) não será um extremante local, neste caso será um ponto de sela de f.
4. Se H(x_0,y_0) = 0 nada podemos afirmar quanto ao ponto (x_0,y_0)

Além disso, se f(x,y) for contínua num conjunto compacto então esta função assumirá um valor de máximo e de mínimo neste conjunto.

3ª Lista de Exercícios Resolvidos sobre Máximos e Mínimos

1) Nos exercícios abaixo determine e classifique os pontos estacionários das funções dadas abaixo:

a) f(x,y) = xy(x+y-1)

SOLUÇÃO: Procuramos localizar os pontos críticos da função ao resolver o sistema $$ \frac{\partial f}{\partial x} = 2xy + y^2 -y= 0$$ $$ \frac{\partial f}{\partial y} = x^2 +2xy – x = 0.$$

Da segunda equação: $$ x^2 + x (2y -1) = x[x+(2y-1)]=0 \Rightarrow x=0 \;\;\; ou \;\;\; x = -2y +1.$$

E substituindo as duas possibilidades na primeira equação encontramos quatro pontos $$A(0,0), B(1,0), C ( 0 ,1), D \left( \frac{1}{3} ,  \frac{1}{3} \right) .$$

Observando que $$H(x,y) = 4xy – (2x + 2y -1)^2 $$ $$ \frac{\partial ^2 f}{\partial x^2} (x,y) = 2y $$ então podemos classificar os pontos A, B e C como pontos de sela e o ponto D como ponto de mínimo.

Isso pode ser observado na ilustração abaixo:

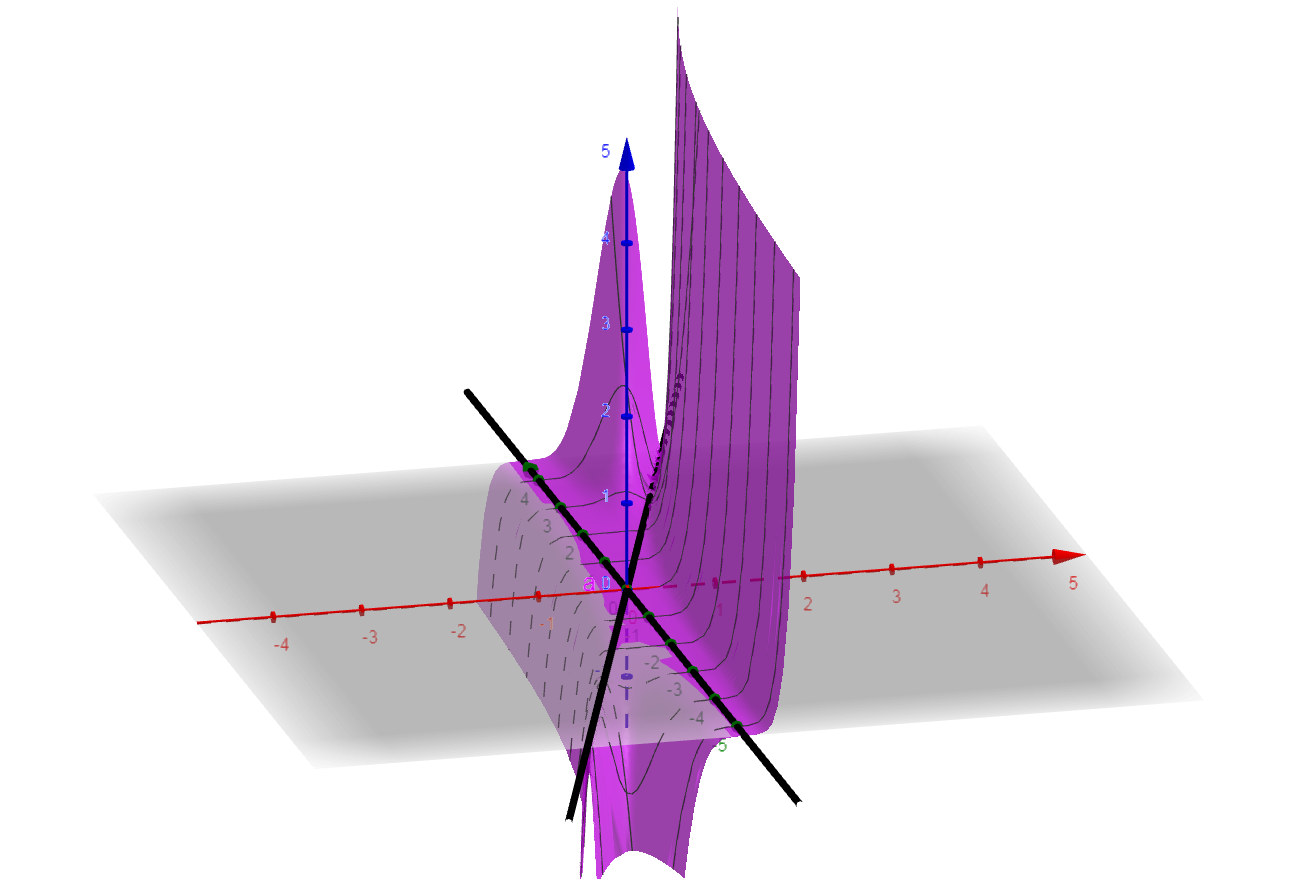
b) f(x,y) = x^5 - (y-3x)^2

SOLUÇÃO: Procuramos localizar os pontos críticos da função ao resolver o sistema $$ \frac{\partial f}{\partial x} = 5\,{x}^{4}\,{y}^{2}-36\,{x}^{5}\,y+63\,{x}^{6} = 0$$ $$ \frac{\partial f}{\partial y} = 2\,{x}^{5}\,\left( y-3\,x\right)  = 0.$$

Por este sistema percebemos que os nossos pontos críticos estão sobre as retas x=0 e y = 3x .

Neste caso, $$H(x,y) = -60\,{x}^{8}\,{y}^{2}+360\,{x}^{9}\,y-540\,{x}^{10}$$ e $$ H(0,y) = H(x,3x) = 0 .$$ Ou seja, em ambos os casos nada podemos concluir. Isso fica claro na imagem abaixo, onde trazemos o gráfico da função e as duas retas.

2) Dada f(x,y) = x^2 - xy +y^2 , determine seus pontos críticos e classifique-os quando possível.

SOLUÇÃO:

Os pontos críticos são dados por $$\frac{\partial f}{\partial x} = 2x-y = 0 \Leftrightarrow y = 2x $$ $$\frac{\partial f}{\partial y} = 2y-x = 0 $$ Usando o resultado da primeira linha na segunda linha obtemos $$ 3x = 0 \Leftrightarrow x = 0 \Leftrightarrow y = 2 \times 0 = 0 \Leftrightarrow P_1(0,0).$$

Logo, obtemos um único ponto crítico.

O Hessiano desta função é dado por H(x,y) = 3 >0 e como \frac{\partial ^2 f}{\partial x^2} (x,y) = 2 >0 , podemos classificar P_1(0,0) como um ponto de mínimo global, como podemos ver no gráfico abaixo

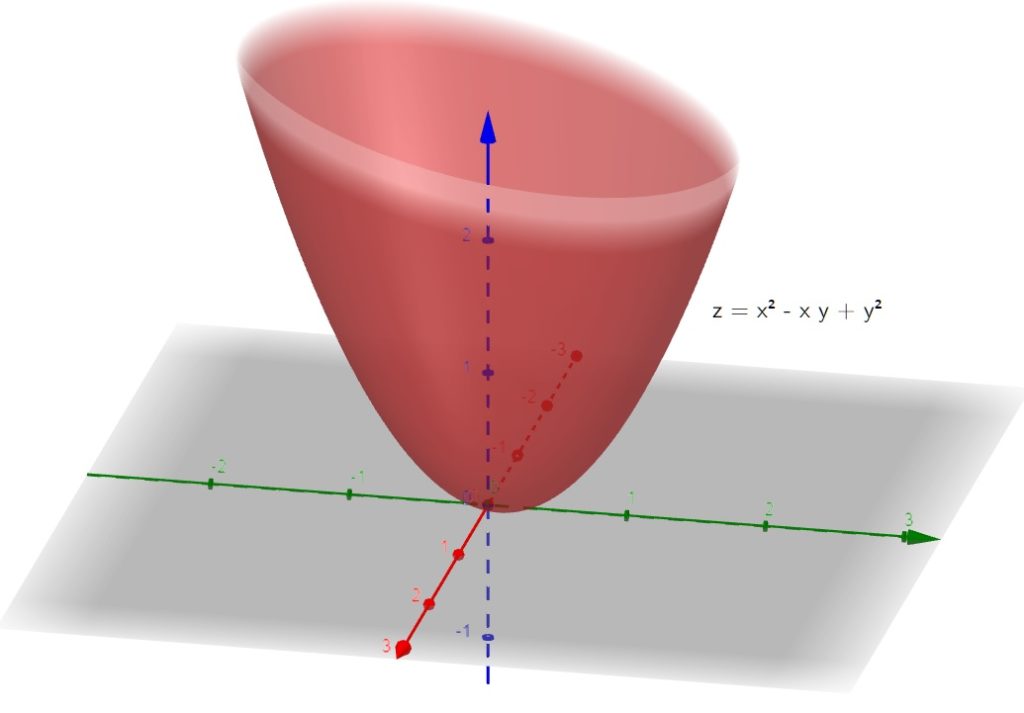
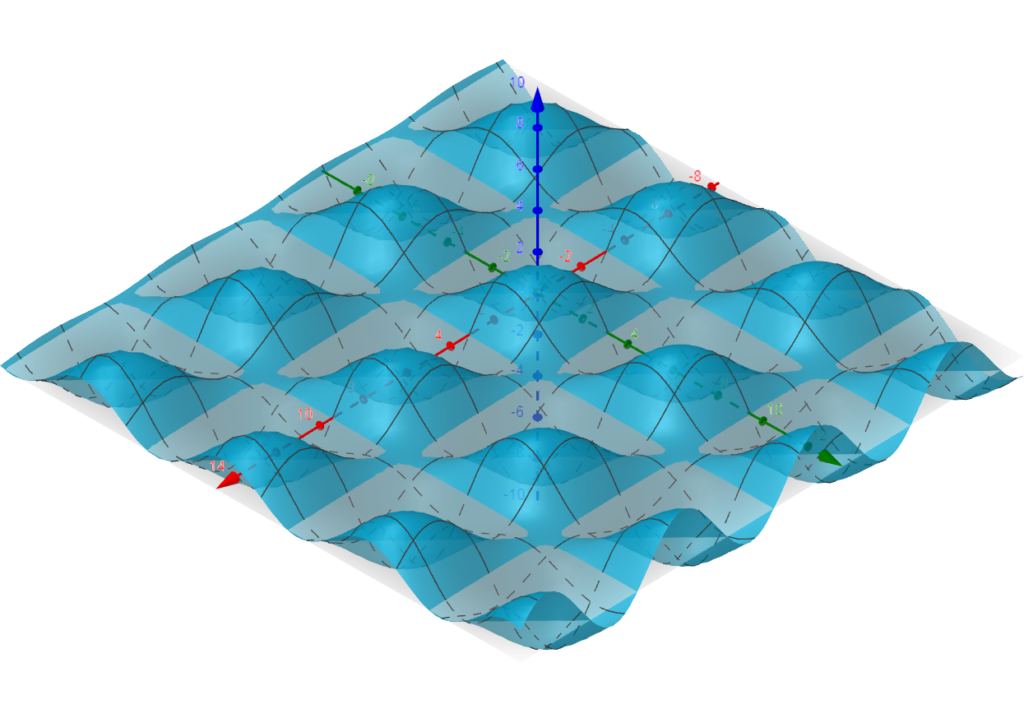
3) Determine os pontos estacionários e verifique os que são de máximo, de mínimo ou pontos de sela, da função f(x,y) = sen(x)+sen(y)+sen(x+y).

SOLUÇÃO: Para encontrar os pontos críticos desta função vamos resolver o sistema: \begin{eqnarray} \frac{\partial f }{\partial x }  & = &  cos(x) + cos(x+y) = 0  \\ \frac{\partial f }{\partial y }  & = & cos(y) + cos(x+y) = 0    \end{eqnarray} Este sistema nos diz que \begin{eqnarray}  cos(x) & = & – cos(x+y)  \\ cos(y) & = & – cos(x+y)  \end{eqnarray}, ou seja, $$cos(x) = cos(y) \Rightarrow x = y . $$ Substituindo x = y em alguma das derivadas parciais acima encontramos $$cos(x) + cos(2x) = 0 \Rightarrow cos(x) = – cos(2x), $$ ou seja, encontraremos os valores $$x_{k_1} = \frac{\pi }{3} + 2k \pi; x_{k_2} = (2k+1) \pi; x_{k_3} = \frac{5 \pi }{3} + 2k \pi;  \qquad k \in \mathbb{Z} $$ que podem ser visualizados no círculo trigonométrico abaixo:

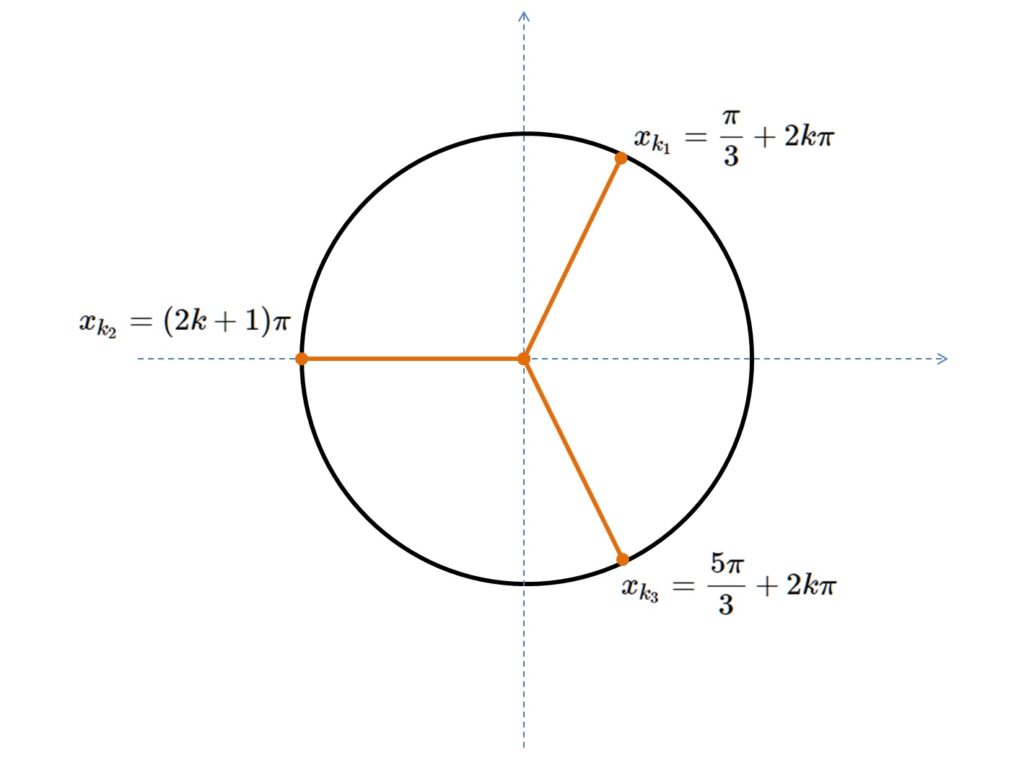
Desta forma teremos infinitos pontos críticos devido à característica periódica da nossa função, estes infinitos pontos críticos podem ser separados em três grupos dados por:  \begin{eqnarray} P_{k_1} & = & \left( \frac{\pi }{3} + 2k \pi ,  \frac{\pi }{3} + 2k \pi  \right) \\ P_{k_2} & = & \left( [2k+1] \pi ,  [2k+1] \pi \right) \\ P_{k_3} & = & \left( \frac{5 \pi }{3} + 2k \pi , \frac{5 \pi }{3} + 2k \pi \right) ; \qquad k \in \mathbb{Z}  \end{eqnarray}

Agora, vamos classificá-los usando o fato de que \begin{eqnarray} \frac{\partial ^2 f }{\partial x ^2 }  & = & -\mathrm{sen}\left( y+x\right) -\mathrm{sen}\left( x\right) \\ H(x,y) & = & \left( -\mathrm{sen}\left( y+x\right) -\mathrm{sen}\left( x\right) \right) \,\left( -\mathrm{sen}\left( y+x\right) -\mathrm{sen}\left( y\right) \right) -{\mathrm{sen}\left( y+x\right) }^{2} \\ & = & \left( \mathrm{sen}\left( y\right) +\mathrm{sen}\left( x\right) \right) \,\mathrm{sen}\left( y+x\right) +\mathrm{sen}\left( x\right) \,\mathrm{sen}\left( y\right) \end{eqnarray} e como nos nossos pontos críticos x = y, podemos escrever  \begin{eqnarray} \frac{\partial ^2 f }{\partial x ^2 }  & = & -\mathrm{sen}\left( 2\,x\right) -\mathrm{sen}\left( x\right) \\ H(x,y) & = & 2\,\mathrm{sen}\left( x\right) \,\mathrm{sen}\left( 2\,x\right) +{\mathrm{sen}\left( x\right) }^{2}\end{eqnarray}

Para os pontos P_{k_1} temos que: $$ H \left( \frac{\pi }{3} + 2k \pi ,  \frac{\pi }{3} + 2k \pi  \right) = 9/4 > 0; \qquad \frac{\partial ^2 f }{\partial x ^2 } \left( \frac{\pi }{3} + 2k \pi ,  \frac{\pi }{3} + 2k \pi  \right) = – \sqrt{3} <0 ,$$ portanto, estes serão pontos de máximo.

Para os pontos P_{k_2} temos que: $$ H \left( [2k+1] \pi ,  [2k+1] \pi \right) = 0, $$ logo, nada podemos concluir.

Para os pontos P_{k_3} temos que: $$ H \left( \frac{5 \pi }{3} + 2k \pi , \frac{5 \pi }{3} + 2k \pi \right) = 9/4 > 0; \qquad \frac{\partial ^2 f }{\partial x ^2 } \left( \frac{\pi }{3} + 2k \pi ,  \frac{\pi }{3} + 2k \pi  \right) = \sqrt{3} >0 ,$$ portanto, estes serão pontos de mínimo.

O gráfico desta função pode ser visto abaixo:

Leia Mais:

• Máximos e Mínimos de Funções de Várias Variáveis
• Máximos e Mínimos de Campos Escalares | 2ª Lista de Exercícios Resolvidos
• Máximos e Mínimos de Campos Escalares | 1ª Lista de Exercícios Resolvidos
• Maximos e Mínimos: O Método dos Multiplicadores de Lagrange

Assista Nossa Vídeo-Aula Sobre Máximos e Mínimos: