Como multiplicar matrizes? Um guia passo a passo com exemplos

Aprenda os fundamentos da multiplicação de matrizes com teoria e exemplos de uma forma simples e direta.

A multiplicação de matrizes é um processo de combinação de duas matrizes para produzir uma terceira matriz. É uma ferramenta importante usada em muitos aspectos da matemática e da ciência e pode ser usada para resolver sistemas de equações lineares ou calcular transformações no espaço-tempo.

O que é uma matriz?

Uma matriz A, m \times n (lê-se: m por n), é uma tabela de m \cdot n números dispostos em m linhas e n colunas. Desta forma, representamos uma matriz colocando a tabela dentro de parênteses ou de colchetes, ou ladeado a tabela, à esquerda e à direita, por duas barras verticais, do seguinte modo: $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right] .$$

Neste sentido, podemos estabelecer que a i- ésima linha de A é dada por $$\left[ \begin{array}{cccc} a_{i1} & a_{i2} & \ldots & a_{in} \end{array} \right]$$para j = 1, . . . ,n e a j- ésima coluna de A é $$\left[ \begin{array}{cccc} a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj}\\ \end{array} \right] .$$ Dizemos que a_{ij} é o elemento ou a entrada de posição i,j da matriz A.

Indicaremos por \mathbb{M}_{m \times n} \left( \mathbb{R} \right) como o conjunto das matrizes reais de ordem m \times n. Se m = n, ao invés de \mathbb{M}_{n \times n} \left( \mathbb{R} \right) usa-se a notação \mathbb{M}_{n} \left( \mathbb{R} \right) .

Multiplicação: Como calcular o produto de matrizes?

Para que duas matrizes sejam compatíveis para multiplicação, o número de colunas na primeira matriz deve ser igual ao número de linhas na segunda matriz. Ao realizar a multiplicação de matrizes, cada elemento em uma matriz é multiplicado por todos os elementos na outra matriz e, em seguida, somados para formar um valor resultante para essa posição na matriz de saída. Mas antes, vamos falar sobre o produto de um escalar por uma matriz.

Multiplicação de uma matriz por um número (ou escalar)

O produto da matriz A pelo número real \alpha é dada pela multiplicação de \alpha por cada entrada da matriz A. Desta forma, matricialmente, sendo A \in \mathbb{M}_{m \times n} , dada por $$ A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{array} \right]$$ e \alpha \in \mathbb{R} , esta operação transforma cada par ( \alpha , A) \in \left( \mathbb{R} , \mathbb{M}_{m \times n} \right) em uma matriz \alpha A \in \mathbb{M} _{m \times n} , que é dada por $$ \alpha \cdot A = \left[ \begin{array}{cccc} \alpha a_{11} & \alpha a_{12} & \ldots & \alpha a_{1n} \\ \alpha a_{21} & \alpha a_{22} & \ldots & \alpha a_{2n} \\ \vdots & \ddots & \cdots & \vdots \\ \alpha a_{m1} & \alpha a_{m2} & \cdots & \alpha a_{mn}\\ \end{array} \right] .$$

Exemplo: 3 \times \left[ \begin{array}{cccc} 1 & 0 & 78 \\ 0 & 7 & 0 \\ \end{array} \right]=\left[ \begin{array}{cccc} 3 & 0 & 234 \\ 0 & 21 & 0 \\ \end{array} \right].

Propriedades do produto de um escalar por uma matriz

Sendo A é B matrizes m \times n e \alpha , \beta números reais, valem as seguintes propriedades.

1. 1 \times A = A;
2. (-1)\times A =- A, ou seja, a matriz oposta de A é ela mesma multiplicada pelo escalar -1 ;
3. \alpha \times 0=0, ou seja, qualquer constante real multiplicada pela matriz nula ainda gera a matriz nula;
4. 0 \times A=0, ou seja, qualquer matriz multiplicada pela constante zero se torna a matriz nula;
5. (\alpha \beta ) A = \alpha ( \beta A ) = \beta ( \alpha A );
6. ( \alpha + \beta ) A = \alpha A + \beta A ;
7. \alpha ( A + B ) = \alpha A + \alpha B ;
8. \left( \alpha A \right)^{T}  = \alpha A^{T} .

EXEMPLO: Dadas A^{T} = [ 20 \;\;\; 12 \;\;\; 5] , B^{T} = [ 8 \;\;\; 2 \;\;\; 10] e C^{T} = [ -10 \;\;\; 0 \;\;\; -8] , vamos determinar a matriz X tal que $$2A-B+2X +C = 0.$$

Primeiramente, observe que algebricamente temos $$ 2A-B+2X +C = 0 \Leftrightarrow 2X = -2A+B – C \Leftrightarrow X = -A + \frac{1}{2} B – \frac{1}{2} C.$$ Portanto, substituindo as matrizes A,B, \text{ e } C , encontramos $$ X = -A + \frac{1}{2} B – \frac{1}{2} C = \left[ \begin{array}{cccc} -20 \\ -12 \\ -5 \\ \end{array} \right] + \frac{1}{2} \left[ \begin{array}{cccc} 8 \\ 2 \\ 10 \\ \end{array} \right] – \frac{1}{2} \left[ \begin{array}{cccc} -10 \\ 0 \\ -8 \\ \end{array} \right] = \left[ \begin{array}{cccc} -11 \\ -11 \\ 4 \\ \end{array} \right] .$$

Multiplicação de Matrizes

Assim se A = (a_{ij})_{m×p} e B = (b_{ij})_{p×n} o produto entre A e B é definido pela matriz de ordem m × n $$C = AB$$ obtida da seguinte forma: $$c_{ij} = a_{i1} b_{1j} + a_{i2} b_{2j} + . . . + a_{ip} b_{pj},$$ para i = 1, . . . ,m e j = 1, . . . , n.

Matricialmente, temos que:

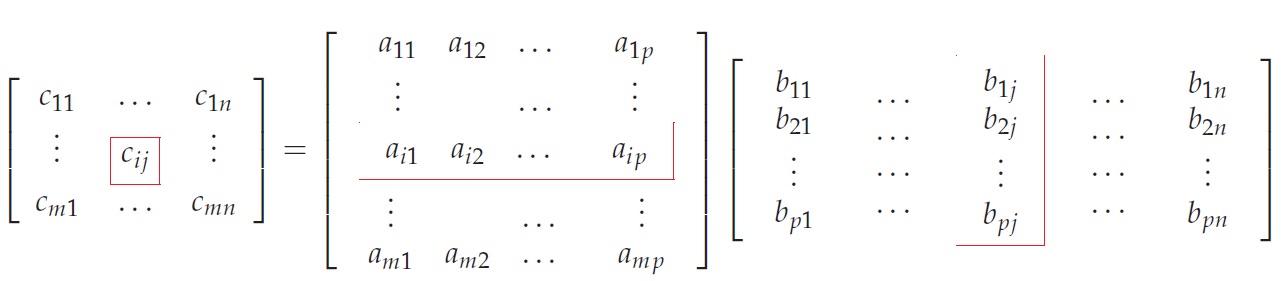
OBSERVAÇÕES: 

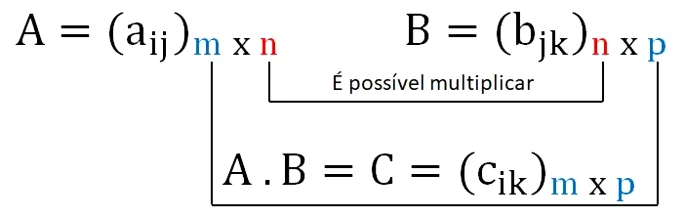
1. Pela definição podemos concluir que o produto de duas matrizes só existe quando o número de colunas da primeira matriz é igual ao número de linhas da segunda matriz;
2. Podemos concluir que o número de linhas da matriz-produto é igual ao número de linhas da primeira matriz e o número de colunas da matriz-produto é o número de colunas da segunda matriz;

A imagem abaixo ilustra estas duas observações quanto ao produto de matrizes:

EXEMPLO: Dadas as matrizes A=\left[ \begin{array}{cccc} 2 & 1 \\ 3 & 4 \\ 5 & 6 \\ \end{array} \right] e B=\left[ \begin{array}{cccc} 7 & 8 & 0 \\ 10 & 5 & -2 \\ \end{array} \right] temos que:

1) Existe o produto A \times B , pois o número de colunas de A é igual ao número de linhas de B e A \times B é de ordem 3:

2) Existe o produto B \times A , pois o número de colunas de B é igual ao número de linhas de A e B \times A é de ordem 2:

OBSERVAÇÃO: É importante observar que nem sempre conseguimos executar os produtos A \times B e  B \times A . Além disso, quando estes produtos existe, em geral, A \times B \neq B \times A , ou seja, os produto entre matrizes não é comutativo. Quando A \times B = B \times A , dizemos que estas matrizes são comutativas. 

EXEMPLO: Vamos determinar as matrizes que comutam com A=\left[ \begin{array}{cccc} 1 & 1 \\ 0 & 1 \\ \end{array} \right].

Considere uma matriz B que comuta com A. Neste caso, B precisa ser quadrada e de ordem 2. Seja B=\left[ \begin{array}{cccc} x & u \\ y & v \\ \end{array} \right]. Então, temos que $$ A \times B = B \times A = \left[ \begin{array}{cccc} 1 & 1 \\ 0 & 1 \\ \end{array} \right] \times \left[ \begin{array}{cccc} x & u \\ y & v \\ \end{array} \right] = \left[ \begin{array}{cccc} x & u \\ y & v \\ \end{array} \right] \times \left[ \begin{array}{cccc} 1 & 1 \\ 0 & 1 \\ \end{array} \right] \Leftrightarrow $$ $$ \Leftrightarrow \left[ \begin{array}{cccc} x + y & u + v \\ y & v \\ \end{array} \right] = \left[ \begin{array}{cccc} x  & u + x \\ y & v + y \\ \end{array} \right]$$ o que nos leva ao sistema de equações $$ x+y = x \Leftrightarrow y = 0 \\ u+v = x+u \Leftrightarrow v = x \\ v = y +v \Leftrightarrow y = 0 .$$

Portanto, toda matriz na forma $$ B=\left[ \begin{array}{cccc} x & u \\ 0 & x \\ \end{array} \right], \forall x,u \in \mathbb{R}$$ comuta com a matriz A .

Propriedades da Multiplicação de Matrizes:

Considerando matrizes A, B e C de forma conveniente e
\alpha \in \mathbb{R}, são válidas as seguintes propriedades:

1. (A.B).C=A.(B.C)
2. C.(A+B)=C.A+C.B. Cuidado: Mantenha sempre a ordenação original, C.(A+B) \neq A.C + C.B ou C.(A+B) \neq C.A + B.C ou C.(A+B) \neq A.C + B.C.
3. A.I=I.A=A
4. (\alpha . A).B = A. (\alpha B) = \alpha (A.B)
5. A. 0=0.A=0
6. (A.B)^T= B^T. A^T
7. A lei do cancelamento nem sempre é válida para a multiplicação de matrizes, ou seja, A.B=A.C não significa que B=C.
8. Se as matrizes A e B não comutam, então, (A+B)^2 \neq A^2 + 2AB +B^2

Leia Mais Artigos Sobre Matrizes

• Matrizes – Definições Básicas e Primeiros Exemplos
• Estes são os 10 Principais Tipos de Matrizes na Matemática
• Como Somar Matrizes? Um guia passo a passo com exemplos
• O que é o Jacobiano? E como calcular a Matriz Jacobiana?
• Matemática Comercial Básica | 36 Exercícios Resolvidos