A Integral de Fourier | 1ª Lista de Exercícios Resolvidos

A Integral de Fourier é uma extensão das Séries de Fourier que permite obter expansões de funções que não são periódicas. A Integral de Fourier de uma função f definida no intervalo (-\infty, \infty) é dada por $$f(x) = \frac{1}{\pi}\int\limits_{0}^{\infty}{\left[ A(\alpha)\cos{(\alpha x)}+B(\alpha)\sin{(\alpha x)}\right]d\alpha}$$ onde $$A(\alpha) = \int\limits_{-\infty}^{\infty}{f(x)\cos{(\alpha x)}dx}\;\;\;e\;\;\;B(\alpha) = \int\limits_{-\infty}^{\infty}{f(x)\sin{(\alpha x)}dx}.$$

A Integral de Fourier vale se x é ponto de continuidade de f(x) . Se x é o ponto de descontinuidade, devemos substituir f(x) por \dfrac{f(x+0) + f(x-0) }{2}, sendo f(x+0) o limite de f(x) à direita de x e f(x-0) o limite de f(x) à esquerda de x.

1ª Lista de Exercícios Resolvidos Sobre a Integral de Fourier

1) Prove que: a) \lim\limits_{ \alpha \rightarrow \infty}{\int \limits_{0}^{L}{\dfrac{sen ( \alpha v)}{v}dv}} = \dfrac{\pi}{2}; b) \lim\limits_{ \alpha \rightarrow \infty}{\int \limits_{-L}^{0}{\dfrac{sen ( \alpha v)}{v}dv}} = \dfrac{\pi}{2}

SOLUÇÃO: Seja \alpha v = y.

Então $$ \lim\limits_{ \alpha \rightarrow \infty}{\int \limits_{0}^{L}{\frac{sen ( \alpha v)}{v}dv}} = \lim\limits_{ \alpha \rightarrow \infty}{\int \limits_{0}^{\alpha L}{\frac{sen ( y)}{y}dy}} = \int \limits_{0}^{\infty }{\frac{sen ( y)}{y}dy} = \frac{\pi}{2} $$ o que prova o item (a).

Por um raciocínio análogo, podemos mostrar o item (b).

Seja \alpha v = - y.

$$ \lim\limits_{ \alpha \rightarrow \infty}{\int \limits_{-L}^{0}{\frac{sen ( \alpha v)}{v}dv}} = \lim\limits_{ \alpha \rightarrow \infty}{\int \limits_{0}^{\alpha L}{\frac{sen ( y)}{y}dy}} = \int \limits_{0}^{\infty }{\frac{sen ( y)}{y}dy} = \frac{\pi}{2} .$$

2) Vamos usar a Integral de Fourier para resolver o seguinte problema: Uma barra delgada semi-infinita cuja superfície é isolada, tem temperatura inicial igual a f(x). Em dado instante, aplica-se à extremidade x =0 um temperatura zero, que é então mantida. Queremos solucionar o problema de contorno para a temperatura u(x,t)  num ponto x no instante t.

SOLUÇÃO: O problema de contorno é dado por $$k\frac{\partial ^2 u}{\partial x^2} = \frac{\partial u}{\partial t},\;\;\;\;\; x >0, \;\;\;\;\;t>0,$$ sujeita a $$u(x,0) = f(x), \qquad u(0,t) = 0 , \qquad | u(x,t) | \leq M $$ onde a última condição decorre do fato de a temperatura ser limitada, por motivos físicos.

Usando o método da separação das variáveis, de forma análoga ao que fizemos neste artigo, obtém-se como solução $$u(x,t) = e^{-k \lambda ^2 t} \left( A cos( \lambda x) + B sen( \lambda x) \right) .$$

Da condição u(0,t) = 0 , obtemos A = 0 , de modo que $$u(x,t) = B e^{-k \lambda ^2 t} sen( \lambda x) .$$

Como não há restrições quanto a \lambda podemos substituir B nesta solução por uma função B( \lambda) e ter ainda uma solução.

Além disso, podemos integrar sobre \lambda de 0 a \infty e ainda obter uma solução. Tal processo é análogo ao teorema da superposição para valores discretos de \lambda utilizado nas séries de Fourier. Chegamos assim à solução possível $$ u(x, t) = \int \limits_{0}^{\infty}{B( \lambda ) e^{-k \lambda ^2 t} sen( \lambda x) } d \lambda.$$

Pela condição u(x,0) = f(x) obtemos $$ f(x) = \int \limits_{0}^{\infty}{B( \lambda ) sen( \lambda x) } d \lambda$$ que é uma equação integral para a determinação de B( \lambda ) .

Podemos ver que como f(x) deve ser uma função ímpar, se tem $$ B( \lambda ) = \frac{2}{\pi} \int \limits_{0}^{\infty}{f(x) sen( \lambda x) } d x = \frac{2}{\pi} \int \limits_{0}^{\infty}{f(v) sen( \lambda v) } d v$$

Levando este resultado na solução do problema, encontramos $$u(x, t) = \frac{2}{\pi} \int \limits_{0}^{\infty} {\int\limits_{0}^{\infty}{f(v)  e^{-k \lambda ^2 t}  sen( \lambda x)  sen( \lambda v)  d \lambda} dv}.$$

Usando uma propriedade trigonométrica (item 1) das relações entre seno e cosseno deste artigo) percebemos que $$ sen( \lambda x)  sen( \lambda v) = \frac{1}{2} \left[ cos( \lambda [v-x]) – cos( \lambda [v+x]) \right]$$ o que nos leva a escrever $$u(x, t) = \frac{1}{\pi} \int \limits_{0}^{\infty} {\int\limits_{0}^{\infty}{f(v)  e^{-k \lambda ^2 t}  \left[ cos( \lambda [v-x]) – cos( \lambda [v+x]) \right] d \lambda} dv}=$$ $$ = \frac{1}{\pi} \int \limits_{0}^{\infty} { f(v) \left[ \int\limits_{0}^{\infty}{e^{-k \lambda ^2 t} cos( \lambda [v-x]) d \lambda} – \int\limits_{0}^{\infty}{e^{-k \lambda ^2 t} cos( \lambda [v+x]) d \lambda} \right] dv} $$

Da integral $$ \int_{0}^{ \infty}{e^{-\alpha \lambda ^2} cos ( \beta \lambda ) d \lambda}= \frac{1}{2} \sqrt{\frac{\pi}{2}} e^{-\beta ^2/4 \alpha},$$ que calculamos no exercício 5 deste artigo, decorre $$u(x, t) = \frac{1}{2 \sqrt{ \pi k t }} \left[ \int \limits_{0}^{\infty}{f(v)  e^{- (v – x)^2 / 4 k t } dv} – \int \limits_{0}^{\infty}{f(v)  e^{- (v + x)^2 / 4 k t } dv} \right]$$ fazendo \dfrac{(v-x)}{2 \sqrt{kt} } = w na primeira integral e \dfrac{(v+x)}{2 \sqrt{kt} } = w na segunda integral, obtemos $$u(x, t) = \frac{1}{\sqrt{ \pi }} \left[ \int \limits_{-\frac{x}{2 \sqrt{kt} }}^{\infty}{f(2w \sqrt{kt} + x )  e^{-w^2} dw} – \int \limits_{\frac{x}{2 \sqrt{kt} }}^{\infty}{f(2w \sqrt{kt} – x)  e^{- w^2 } dw} \right]$$

3) Resolva o mesmo problema do exercício anterior para o caso da temperatura inicial de f(x) ser uma constante, u_0 .

Usando o resultado do exercício anterior, ao fazermos f(x,t) = u_0 , obtemos $$u(x, t) = \frac{u_0}{\sqrt{ \pi }} \left[ \int \limits_{-\frac{x}{2 \sqrt{kt} }}^{\infty}{e^{-w^2} dw} – \int \limits_{\frac{x}{2 \sqrt{kt} }}^{\infty}{e^{- w^2 } dw} \right] = $$ $$ = \frac{u_0}{\sqrt{ \pi }}\int \limits_{-\frac{x}{2 \sqrt{kt} }}^{\frac{x}{2 \sqrt{kt} }}{e^{-w^2} dw} = \frac{2 u_0}{\sqrt{ \pi }}\int \limits_{0}^{\frac{x}{2 \sqrt{kt} }}{e^{-w^2} dw}.$$

Lembrando que, como definimos no artigo sobre a Função Erro, ela é denotada por erf(x) , é $$ erf(x) = \frac{2}{\sqrt{ \pi }} \int_{0}^{x}{e^{-u^2} du}, $$ então, obtemos como solução deste problema a relação

$$u(x, t) =  \frac{2 u_0}{\sqrt{ \pi }}\int \limits_{0}^{\frac{x}{2 \sqrt{kt} }}{e^{-w^2} dw} = u_0 erf \left( \frac{x}{2 \sqrt{kt} } \right).$$

4) Esboce o gráfico e determine a representação por uma Integral de Fourier, da função $$ f(x) = \left\{\begin{array}{rl} 0, &x<0 \\ 1, & 0 < x <2 \\ 0, & x>2 \end{array} \right.$$

SOLUÇÃO: 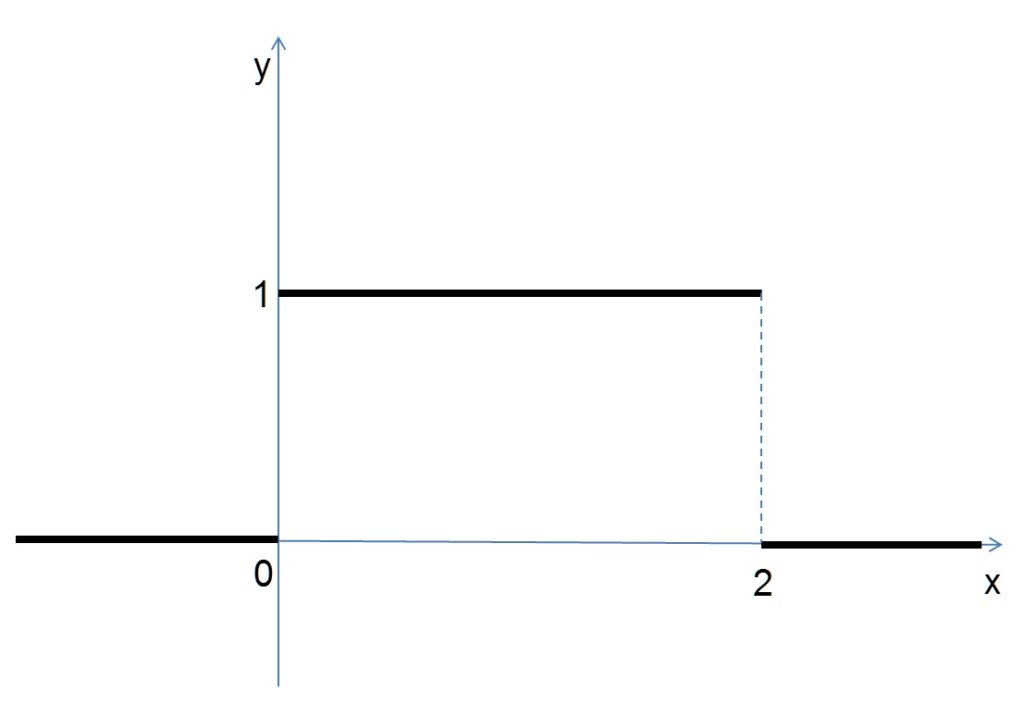A função, cujo gráfico é apresentado na figura abaixo, terá coeficientes da integral de Fourier dada por:

$$A(\alpha) = \int\limits_{- \infty}^{0}{f(x)cos(\alpha x ) dx} + \int\limits_{0}^{2}{f(x)cos(\alpha x ) dx} + \int\limits_{2}^{\infty}{f(x)cos(\alpha x ) dx} = $$ $$ = \int\limits_{0}^{2}{cos(\alpha x ) dx} = \frac{sen( 2 \alpha )}{\alpha}$$ $$ B( \alpha ) = \int\limits_{- \infty}^{\infty}{f(x)sen(\alpha x ) dx}  = \int\limits_{0}^{2}{sen(\alpha x ) dx} = \frac{1 – cos( 2 \alpha )}{\alpha}.$$ Assim, $$f(x) = \frac{1}{\pi}\int\limits_{0}^{\infty}{\left[ \left( \frac{sen( 2 \alpha )}{\alpha} \right)cos(\alpha x) + \left( \frac{1 – cos( 2 \alpha )}{\alpha} \right)sen(\alpha x) \right] d \alpha} = $$ $$ = \frac{2}{\pi}\int\limits_{0}^{\infty}{\frac{sen( \alpha ) cos( \alpha [x-1])}{ \alpha } d \alpha}.$$

Leia Mais:

• Integral de Fourier | Fator Descontínuo de Dirichlet e Integrais de Laplace
  
• A Integral de Fourier | 2ª Lista de Exercícios Resolvidos
• Séries de Fourier | História, Definição e Condições de Existência.
• Uma Introdução à Transformada de Fourier
  

Assista Nossa Vídeo-Aula Sobre a Integral de Fourier