A Integral de Fourier | 2ª Lista de Exercícios Resolvidos

Nesta segunda lista de exercícios sobre a Integral de Fourier queremos aprofundar uma pouco mais na dificuldade dos tópicos e das suas particularidades, inclusive utilizando esta ferramenta para solucionar problemas de valores iniciais e de contorno.

Lembrando que a Integral de Fourier é uma extensão das Séries de Fourier que permite obter expansões de funções que não são periódicas. A Integral de Fourier de uma função f definida no intervalo (-\infty, \infty) é dada por $$f(x) = \frac{1}{\pi}\int\limits_{0}^{\infty}{\left[ A(\alpha)\cos{(\alpha x)}+B(\alpha)\sin{(\alpha x)}\right]d\alpha}$$ onde $$A(\alpha) = \int\limits_{-\infty}^{\infty}{f(x)\cos{(\alpha x)}dx}\;\;\;e\;\;\;B(\alpha) = \int\limits_{-\infty}^{\infty}{f(x)\sin{(\alpha x)}dx}.$$

2ª Lista de Exercícios Sobre Integral de Fourier

1) Determine uma solução limitada da equação de Laplace \nabla ^2 v = 0 para o semi-plano y > 0 , se v toma o valor de f(x) no eixo x , ou seja, v(x,0) = f(x) .

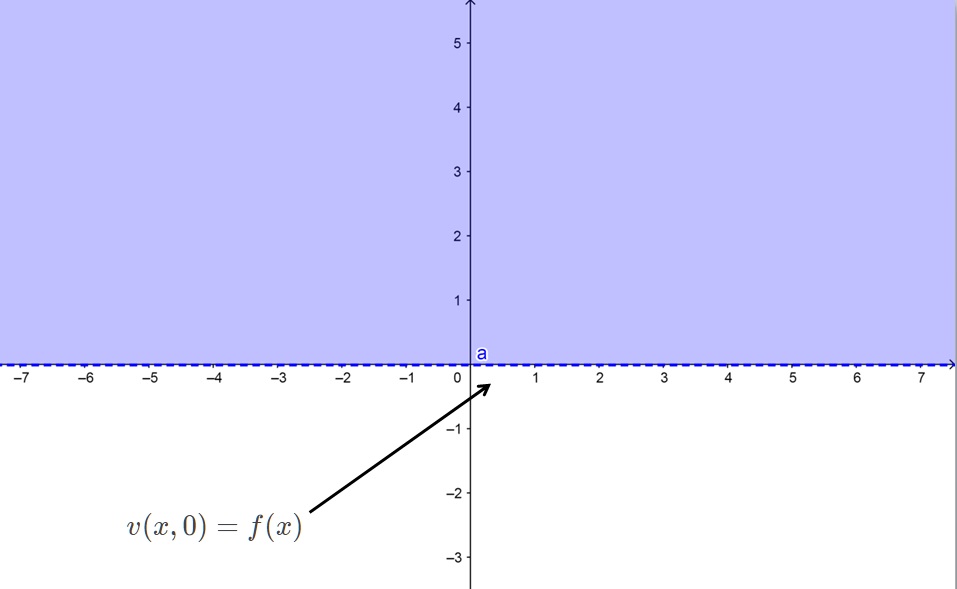
O problema de contorno para a determinação de v(x,y) é dado por $$\frac{\partial ^2 v}{\partial x^2} + \frac{\partial ^2 v}{\partial y^2}=0$$ $$ v(x,0) = f(x); \qquad | v(x,y)| < M . $$

Usaremos o método da separação das variáveis para resolver este problema, fazendo $$v(x,y) = X(x) Y(y)$$ na equação diferencial parcial. Desta forma, assim como feito para a equação da onda unidimensional neste artigo,  encontramos $$\frac{X”}{X} = \frac{\ddot{Y}}{Y} = – \lambda ^2 .$$

O fato de igualharmos a uma constante é imediato, pois temos duas funções dadas em variáveis diferentes que são iguais, logo estas funções só podem ser constantes. A escolha dela como uma constante negativa k = - \lambda ^2 pode ser feita sem perda de generalidade, apenas para sistematizar nossa análise.

Desta forma, obtemos duas equações diferenciais ordinárias, dadas por $$ X” + \lambda ^2 X = 0, \qquad \ddot{Y} – \lambda ^2 Y = 0 $$, que são EDOs de 2ª ordem homogêneas com coeficientes constantes, com soluções dadas por $$ X(x) = a_1 cos (\lambda x ) + b_1 sen ( \lambda x ), \qquad Y(y) = a_2 e^{ \lambda y} + b_2 e^{ – \lambda y}.$$

Então, a solução é $$u(x,y) = \left( a_1 cos (\lambda x ) + b_1 sen ( \lambda x ) \right) \left(  a_2 e^{ \lambda y} + b_2 e^{ – \lambda y} \right).$$

Se \lambda > 0 o termo em e^{\lambda y} é não-limitado quando y \rightarrow \infty ; assim, para manter v(x,y) limitada devemos ter a_2 = 0. O que conduz à solução $$ v(x,y) = e^{- \lambda y} \left[ A cos( \lambda x ) + B sen( \lambda x ) \right] .$$

Como não há restrição sobre \lambda , podemos substituir A por A( \lambda ) , B por B ( \lambda ) , e integrar em relação a \lambda para obter $$ v(x,y) = \int \limits_{0}^{\infty}{e^{- \lambda y} \left[ A cos( \lambda x ) + B sen( \lambda x ) \right] d \lambda} .$$

A condição de contorno v(x, 0) = f(x) dá $$ v(x,0) = \int \limits_{0}^{\infty}{\left[ A cos( \lambda x ) + B sen( \lambda x ) \right] d \lambda} = f(x).$$

Assim, pelo teorema da integral de Fourier $$ A( \lambda ) = \frac{1}{\pi}\int\limits_{- \infty}^{\infty}{f(u)cos( \lambda u ) du}, \qquad B( \lambda ) = \frac{1}{\pi}\int\limits_{- \infty}^{\infty}{f(u)sen( \lambda u ) du}$$

Levando essas expressões para a solução v(x,y) , temos finalmente: $$ v(x,y) = \int \limits_{0}^{\infty}{e^{- \lambda y} \left[ \left( \frac{1}{\pi}\int\limits_{- \infty}^{\infty}{f(u)cos( \lambda u ) du} \right) cos( \lambda x ) + \left( \frac{1}{\pi}\int\limits_{- \infty}^{\infty}{f(u)sen( \lambda u ) du} \right) sen( \lambda x ) \right] d \lambda} = $$ $$ = \frac{1}{\pi} \int\limits_{0}^{\infty}\int\limits_{- \infty}^{\infty}{e^{- \lambda y} f(u)cos( \lambda u ) cos( \lambda x ) du d \lambda} + \frac{1}{\pi} \int\limits_{0}^{\infty}\int\limits_{- \infty}^{\infty}{e^{- \lambda y} f(u)sen( \lambda u ) sen( \lambda x ) du d \lambda } = $$ $$ = \frac{1}{\pi} \int\limits_{0}^{\infty}\int\limits_{- \infty}^{\infty}{e^{- \lambda y} f(u) \left[ cos( \lambda u ) cos( \lambda x ) +sen( \lambda u ) sen( \lambda x ) \right] du d \lambda } .$$ Pelas relações entre seno e cosseno desta lista de propriedades e identidades trigonométricas, encontramos $$ v(x,y) = \frac{1}{\pi} \int\limits_{0}^{\infty}\int\limits_{- \infty}^{\infty}{e^{- \lambda y} f(u)  cos( \lambda [u – x] ) du d \lambda }. $$

Para refinar um pouco mais este resultado vamos observar que $$ v(x,y) = \frac{1}{\pi} \int\limits_{- \infty}^{\infty}{f(u) \left[ \int\limits_{0}^{\infty}{e^{- \lambda y}  cos( \lambda [u – x] ) d \lambda} \right] du }. $$

Por integração elementar, temos $$ \int\limits_{0}^{\infty}{e^{- \lambda y}  cos( \lambda [u – x] ) d \lambda} = \frac{y}{y^2 + (u-x)^2} $$ de modo que a solução do problema é dado por

$$ v(x,y) = \frac{1}{\pi} \int\limits_{- \infty}^{\infty}{ \frac{y f(u) }{y^2 + (u-x)^2} du }. $$

Leia Mais:

• Integral de Fourier | Fator Descontínuo de Dirichlet e Integrais de Laplace
  
• A Integral de Fourier | 1ª Lista de Exercícios Resolvidos
• Séries de Fourier | História, Definição e Condições de Existência.
• Uma Introdução à Transformada de Fourier
  

Assista Nossa Vídeo-Aula Sobre a Integral de Fourier