O que São Histogramas e Polígonos de Frequência? | Estatística

As duas representações gráficas mais utilizadas para distribuições de frequência são os Histogramas e os Polígonos de Frequência. Enquanto um histograma é uma espécie de gráfico de barras que demonstra uma distribuição de frequências, um polígono de Frequência é um gráfico em linha, sendo as frequências marcadas sobre perpendiculares ao eixo horizontal, levando em consideração os pontos médios dos intervalos de classe.

O histograma é usado para analisar a frequência de vezes que as saídas de um processo estão padronizadas, atendendo aos requisitos estabelecidos e qual a variação que elas sofrem. Já o Polígono de Frequência, geralmente, são usados quando se pretende mostrar mais de uma distribuição ou a classificação cruzada de uma variável quantitativa contínua com uma qualitativa ou quantitativa discreta num mesmo gráfico.

Histograma ou Histograma de Frequência

Consiste em um conjunto de retângulos que tem:

1) as bases sobre um eixo horizontal (eixo dos X) com centro no ponto médio e as larguras iguais às amplitudes dos intervalos das classes;

2) As áreas são proporcional às frequências das classes.

Se todos os intervalos tiverem a mesma amplitude, as alturas dos retângulos serão proporcionais às frequências das classes e, então, costuma-se tomar as alturas numericamente iguais a estas frequências. Se os intervalos de classe não tiverem a mesma amplitude, essas alturas deverão ser ajustadas.

Considere, por exemplo, a tabela abaixo é uma distribuição de frequência das alturas de 40 estudantes da Universidade XYZ:

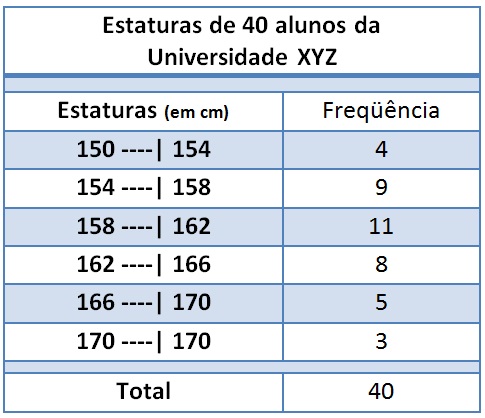
Para a tabela da distribuição de frequência das alturas (em cm) de 40 alunos da Universidade XYZ temos o seguinte Histograma:

Polígono de Frequência

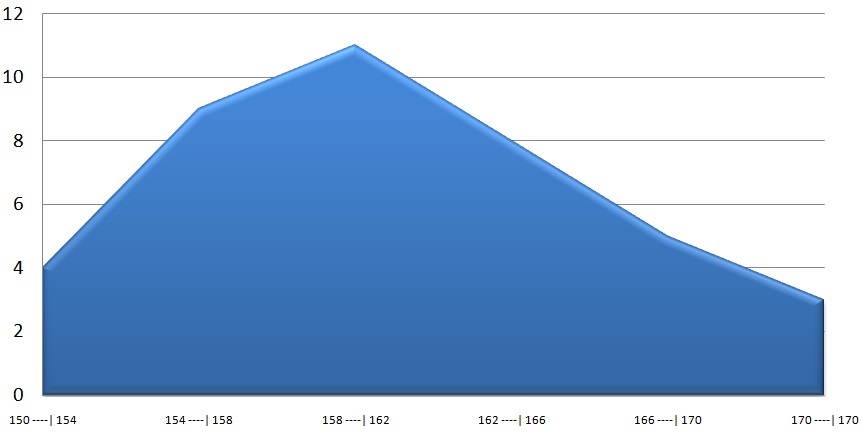
É um gráfico de linha em que as frequências são locadas sobre perpendiculares levantadas nos pontos médios. Pode-se também obtê-los ligando os pontos médios dos topos dos retângulos de um histograma. Para a tabela da distribuição de frequência das alturas (em cm) de 40 alunos da Universidade XYZ temos o seguinte Polígono de Frequência:

Exercício Resolvido sobre Distribuição de Frequência

Considere a tabela abaixo que apresenta a distribuição de frequências do salário de 70 funcionários da empresa KX.

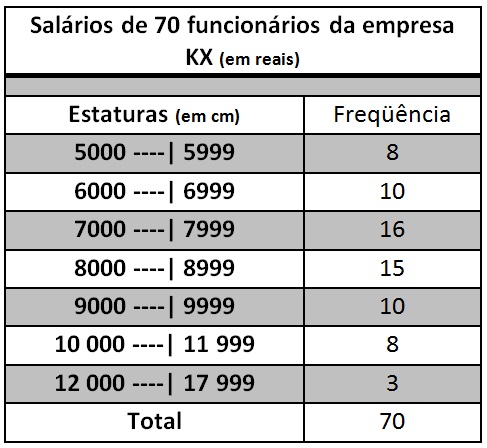
Observe que as duas últimas classes possuem amplitudes diferentes que as outras. Para construir o histograma destes dados devemos lembrar da propriedade de que a áreas devem ser proporcionais às frequências. Note que a primeira e a sexta classes possuem frequências iguais, logo dever ter a mesma área, porém suas bases são diferentes (as amplitudes são diferentes).

A área do retângulo da primeira classe é dado por 8 \times 999=7992, logo 8 multiplicado pela altura do retângulo da sexta classe deve ser 7992\div 1998 = 4. A amplitude da última classe é 5999, sabendo que a medida da área para um frequência igual a 8 é de 7992, por uma regra de três simples obtemos que a área para uma frequência de 3 é igual a 2997. Assim, como a base do retângulo é de 5999 (amplitude da classe) encontramos a altura de \dfrac{2997}{5999}=0,49958326387731288548091348558093\simeq 0,5.

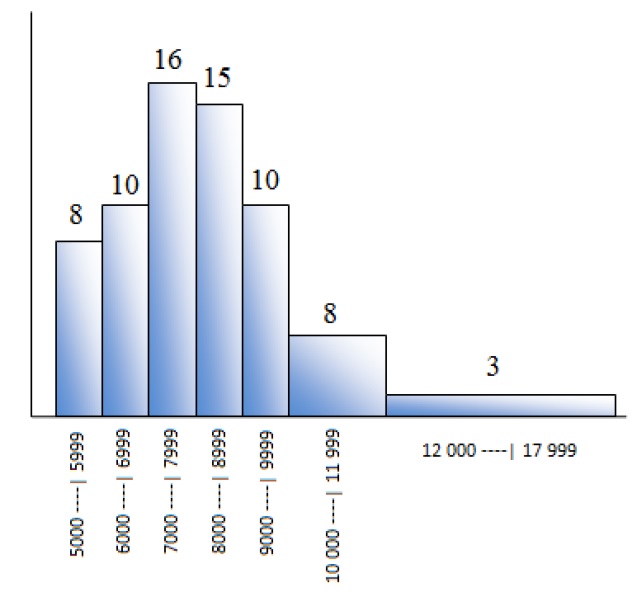
Por fim, o histograma dos dados analisados esta representado pela tabela da distribuição de frequências dos salários de 70 funcionários da empresa KX será dado por:

Leia Mais:

• Distribuições de Frequência Acumulada e Relativa | Estatística
• Conceito Básicos e a diferença entre Estatística Descritiva e Inferência!
• O que é uma Distribuição de Frequências? | Estatística Descritiva
• Gráficos | Da Análise Estatística ao Mercado de Ações