A Função Exponencial Complexa | Funções Analíticas Complexas

Uma função complexa f definida em um subconjunto S \subset \mathbb{R} é uma regra que associa cada z do conjunto S a um número complexo w, denominado valor de f em z. Desta forma, escrevemos $$f(z) = w,$$ onde z é denominada variável complexa, o conjunto S é o domínio da função f. Neste contexto, queremos, explorar a função exponencial complexa.

A Exponencial de um Número Complexo

Sabemos pelo artigo sobre expansão em Série de Potências que \begin{eqnarray*}
e^x & = & \sum_{n=0}^{\infty}{\frac{x^n}{n!}} = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+…. \\
\cos{x} & = & \sum_{n=0}^{\infty}{\frac{(-1)^n x^{2n}}{(2n)!}} = 1- \frac{x^2}{2!}+\frac{x^4}{4!}-…. \\
\sin{x} & = & \sum_{n=0}^{\infty}{\frac{(-1)^n x^{2n+1}}{(2n+1)!}} = x- \frac{x^3}{3!}+\frac{x^5}{5!}-…. \end{eqnarray*}

Considere z=x+yi. Assim,

\begin{eqnarray*}
e^z & = & e^{x+yi} \\
& = & e^x e^{iy} \\
& = & e^x \left( \sum_{n=0}^{\infty}{\frac{(yi)^n}{n!}} \right) \\
& = & e^x \left( 1+yi+\frac{(yi)^2}{2!}+\frac{(yi)^3}{3!}+…. \right) \\
& = & e^x \left( 1+yi-\frac{(y)^2}{2!}-i\frac{(y)^3}{3!}+\frac{(y)^4}{4!} + i \frac{(y)^5}{5!}+…. \right) \\
& = & e^x \left( 1-\frac{y^2}{2!}+\frac{(y)^4}{4!} -\frac{y^6}{6!}…. \right) + e^x \left( y-\frac{y^3}{3!}+\frac{y^5}{5!} -\frac{y^7}{7!}…. \right)i\\
& = & e^x (\cos{y} + i \sin{y})
\end{eqnarray*}

EXEMPLO Calcule exp{(3 + 7 \pi i)}. Pela fórmula da exponencial $$exp{(3 + 7 \pi i)} = e^3 \left( \cos{7 \pi} + i \sin{7\pi} \right) = e^3 \left( -1 \right) = -e^3.$$

Propriedades da Exponencial de um Número Complexo

Da definição da exponencial complexa e^{z} que acabou de ser enunciada, e das propriedades das funções e^x, \sin{x} e \cos{x}, decorrem as seguintes propriedades da exponencial:

1. e^{z_1} e^{z_2} = e^{z_1 + z_2}
2. e^{-z} =\frac{1}{e^{z}}
3. \left( e^z \right)^n = e^{nz}; n inteiro.
4. e^z \neq 0, \forall z;
5. \left| e^{z} \right| = e^{Re(z)}
6. e^z = 1 \Leftrightarrow z= 2k\pi i, k inteiro.

OBSERVAÇÕES:

1. Se considerarmos z escrito a sua forma polar, então e^z assume sua forma compacta dada por $$e^z = r e^{i \theta}.$$
2. Muitas vezes, quando o expoente é muito carregado utilizamos a notação exp (z). Por exemplo, costuma-se escrever $$exp \left[\frac{z}{2} \left( t – \frac{1}{t}\right) \right]$$ em vez de $$e^{\frac{z}{2} \left( t – \frac{1}{t}\right)}.$$

A Função Exponencial Complexa

A função exponencial é definida como f(z) = e^z, ou seja, como descrito anteriormente f(z) = e^z = e^x \left(\cos{y} + i \sin{y} \right). Iremos indicar nossa função exponencial pela notação $$\exp{z} = e^x \left(\cos{y} + i \sin{y} \right)$$ se considerarmos z=x+iy. Desta forma, podemos estabelecer para a função exponencial que:

1. f(z) = \exp{z} é analítica para todo z.De fatos, pois as equações de Cauchy-Riemann para e^x \left(\cos{y} + i \sin{y} \right) se verificam: $$\frac{\partial u}{\partial x} = e^x cos(y) = \frac{\partial v}{\partial y}\;\;\;e\;\;\;\frac{\partial u}{\partial y} = – e^x sen(y) = -\frac{\partial v}{\partial x}.$$
2. f'(z) = \exp{z} De fato, temos que \begin{eqnarray*} (\exp{z})’& = & \dfrac{\partial u}{\partial x} + \dfrac{\partial u}{\partial y} \\ & = & \dfrac{\partial}{\partial x} (e^x \cos{y}) + i \dfrac{\partial }{\partial x}(e^x \sin{y})\\ & = &(e^x \cos{y}) + i (e^x \sin{y})\\ & = & \exp{z}\\ \end{eqnarray*}
3. A forma polar de um número complexo, z= r (\cos{\theta} + i \sin{\theta}) pode ser escrita na forma $$z = r\exp{(\theta i)}.$$
4. A função complexa \exp{z} é periódica, com período 2 \pi i. De fato, $$\exp{z + 2 \pi i} = e^x (\cos{(y+2 \pi)} + i \sin{(y+2 \pi)}) = e^x (\cos{y} + i \sin{y}) = \exp{z}.$$

EXEMPLO: Calcule \left( \exp{iz} \right)' $$\left( \exp{iz} \right)’ = \left( \exp{ix-y} \right)’ = \left( e^{-y}\left( \cos{x} + i \sin{x} \right) \right)’ = \dfrac{\partial}{\partial x} (e^{-y}\cos{x}) + i\dfrac{\partial}{\partial x} e^{-y} \sin{x} =$$ $$= -(e^{-y}\sin{x}) + i (e^{-y}\cos{x}) = i e^{-y}\left( \cos{x} + i \sin{x} \right) = i \exp{iz}$$

EXEMPLO: Para uma função real y=e^{f(x)}, temos que y' = f'(x)e^{f(x)}. Será que $$(exp{(f(z))})’=f'(z)exp{(f(z))},$$ sendo f uma função analítica?

Considerando f(z) = u(x,y)+iv(x,y), temos que $$exp{(f(z))}= exp{(u(x,y)+iv(x,y))} = e^{u(x,y)}\left( \cos{(v(x,y))} + i \sin{(v(x,y))} \right) = $$ $$=e^{u(x,y)}\cos{(v(x,y))} + i e^{u(x,y)} \sin{(v(x,y))}.$$

Considere $$U(x,y) = e^{u(x,y)}\cos{(v(x,y))}$$ e $$V(x,y) = e^{u(x,y)} \sin{(v(x,y))},$$ ou seja, $$\exp{(f(z))} = U(x,y)+iV(x,y).$$ Dái, $$[\exp{(f(z))}]’ = \frac{\partial U}{\partial x}(x,y)+i\frac{\partial V}{\partial x}(x,y),$$ onde
\begin{eqnarray*}
\frac{\partial U}{\partial x}(x,y) & = & e^{u(x,y)}\frac{\partial u}{\partial x} \cos{v(x,y)} – e^{u(x,y)}\frac{\partial v}{\partial x} \sin{v(x,y)}\\
\\
i\frac{\partial V}{\partial x}(x,y) & = &i e^{u(x,y)}\frac{\partial u}{\partial x} \sin{v(x,y)} + ie^{u(x,y)}\frac{\partial v}{\partial x} \cos{v(x,y)}\\
\end{eqnarray*}

Por consequência,
\begin{eqnarray*}
\frac{\partial U}{\partial x}(x,y)+i\frac{\partial V}{\partial x}(x,y) & = & e^{u(x,y)} \frac{\partial u}{\partial x} \left[ \cos{v(x,y)} + i \sin{v(x,y)} \right] + \\
& & + e^{u(x,y)}\frac{\partial v}{\partial x} \left[ – \sin{v(x,y)} + i \cos{v(x,y)} \right] \\
& = & e^{u(x,y)} \frac{\partial u}{\partial x} \left[ \cos{v(x,y)} + i \sin{v(x,y)} \right] + \\
& & + e^{u(x,y)} i \frac{\partial v}{\partial x} \left[ i \sin{v(x,y)} + \cos{v(x,y)} \right] \\
& = & e^{u(x,y)} f'(z) \left[ \cos{v(x,y)} + i \sin{v(x,y)} \right] \\
& = & e^{f(z)} f'(z)\\
\end{eqnarray*}

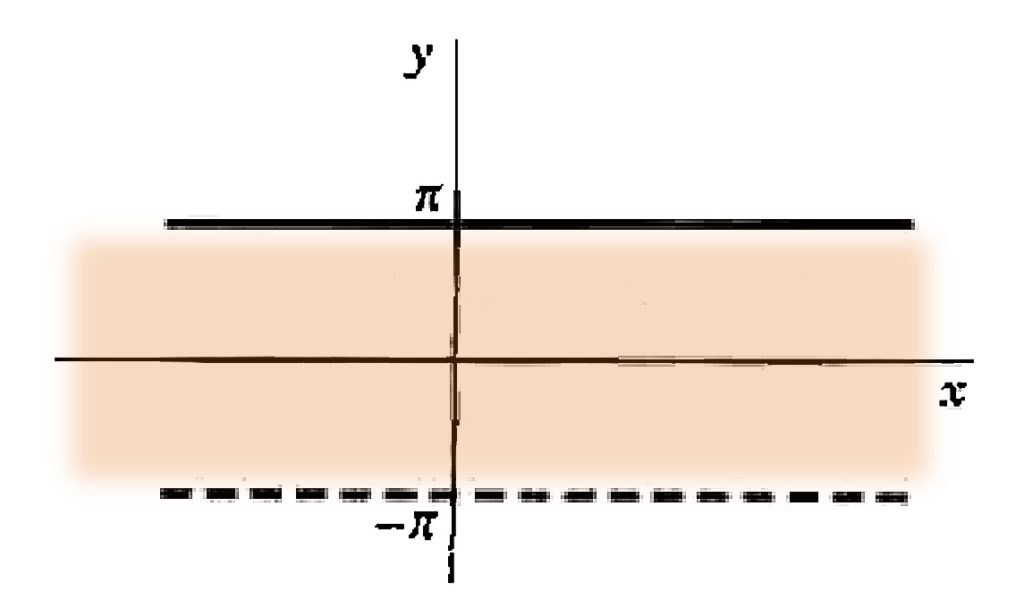
Pode-se mostrar ainda que a função exponencial complexa é periódica, observando que $$ e^{z + 2 \pi i } = e^{z} e^{2 \pi i } = e^{z}, $$ o que mostra que esta função tem período 2 \pi i . Logo, pode expandir esta definição para $$ e^{z \pm 2 n \pi i } =  e^{z}, \qquad (n =0,1,2,3,…)$$ e por causa desta periodicidade, todos os valores os quais w = e^z pode assumir estão na faixa $$ – \pi < y \leq \pi $$ que é chamada de região fundamental da função e^z .

Leia Mais:

• A Função Logarítmica Complexa | Funções Analíticas Complexas
• Variáveis Complexas | Diferenciabilidade e Funções Analíticas
• Funções Analíticas Complexas | Funções Trigonométricas e Hiperbólicas
• Polinômios Complexos | Funções Analíticas Complexas

Referências Bibliográficas:

1. KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.
2. ÁVILA, Geraldo S. S. Variáveis Complexas e Aplicações. 3ª Edição. Rio de Janeiro: LTC, 2000.
3. ZILL, Dennis G. “Curso Introdutório à Análise Complexa com Aplicações”. 2ª edição, LTC, Rio de Janeiro, 2011