Eliminação Gaussiana: Resolvendo sistemas lineares por escalonamento

Um guia completo de como resolver sistemas lineares, usando a eliminação gaussiana ou escalonamento. Aprenda a resolver seu sistema de equações lineares com facilidade e confiança!

Resolver sistemas lineares pode ser uma tarefa confusa, mas com orientação e prática adequadas é possível até se divertir com o estudo. Neste tutorial, você aprenderá como resolver sistemas de equações lineares usando a Eliminação Gaussiana, conhecida também como escalonamento, dando a você a confiança necessária para lidar com qualquer sistema linear com facilidade.

O que é um Sistema Linear?

Um sistema de equações lineares ou sistema linear é um conjunto formado por duas ou mais equações lineares. Um sistema linear pode ser representado na forma: $$ \left\{ \begin{array}{lll} a_{11} x_1 + a_{12} x_2 +…+a_{1n} x_n & = & b_1\\ a_{21} x_1 + a_{22} x_2 +…+a_{2n} x_n & = & b_2\\ \vdots \\ a_{m1} x_1 + a_{m2} x_2 +…+a_{mn} x_n & = & b_m\\ \end{array} \right.  \qquad (1)$$ onde, cada um dos a_{ij}são os coeficientes, x_i são as incógnitas e b_i são os termos independentes. Uma sequencia de números (r_1,r_2,...,r_n), chamada é solução do sistema linear acima se satisfaz todas as equações do sistema ao mesmo tempo. Se m = n dizemos que o sistema linear é de ordem n .

EXEMPLO: Dado o sistema $$ \left\{ \begin{array}{lll} 2x-y+z & = & 1\\ x+2y & = & 6\\ \end{array} \right. $$ uma solução deste sistema é (0,3,4). Notemos que essa solução não é única: a terna \left( \dfrac{8}{5} , \dfrac{11}{5} , 0 \right) também é solução deste sistema.

Classificação de Sistemas Lineares

O número de soluções de um sistema linear determina a sua classificação de duas maneiras com relação à sua consistência:

1. Sistema possível ou consistente: Quando tem pelo menos uma solução. Se tem uma única solução, o sistema é determinado. Se tem mais que uma solução, o sistema é indeterminado.
2. Sistema impossível ou inconsistente: Se não admite qualquer solução. Dois sistemas são equivalentes se admitem a mesma solução. Dois sistemas S_1 e S_2 equivalentes são denotados por S_1 \sim S_2.

Como Fazer a Discussão (ou Estudo) de um Sistema Linear?

Suponhamos que um sistema tenha sido escalonado e, retiradas as equações do tipo 0 = 0 , restam p equações com n incógnitas.

(I) Se a última das equações restantes é $$ 0 x_1 + .\; . \; . + o x_n = \beta _p ; \qquad \left( \beta _p \neq 0 \right) $$ então o sistema é impossível;

Caso contrário, sobram duas alternativas:

(II) Se p = n o sistema é possível e determinado;

(III) Se p < n o sistema é possível e indeterminado;

OBSERVAÇÃO:

1. Outra nomenclatura para um sistema possível ou consistente é sistema compatível. Logo, um sistema impossível ou inconsistente, também, pode ser referenciado como sistema incompatível.
2. Em geral, sistemas lineares com um número maior de incógnitas do que equações só pode ser impossível ou possível e indeterminado.

EXEMPLO: Olhando novamente para o sistema $$ \left\{ \begin{array}{lll} 2x-y+z & = & 1\\ x+2y & = & 6\\ \end{array} \right. $$ podemos afirmar que ele é possível e indeterminado.

Sistemas Lineares: O Caso Geral

Chamamos de sistema linear m \times n ao sistema que possui m equações lineares e n incógnitas. Por exemplo:

1. \left\{ \begin{array}{lll} x-2y +3z& = & 5\\ x+y-z & = & 2\\ \end{array} \right. é um sistema de 2 \times 3;
2. \left\{ \begin{array}{lll} x+3y +-2z+t& = & 0\\ x+2y-3z+t & = & 2\\ x-y-z+t & = & 5\\ \end{array} \right. é um sistema de 3 \times 4;
3. \left\{ \begin{array}{lll} x+2y& = & 1\\ x-y & = & 4\\ 2x-3y & = & 0\\ \end{array} \right. é um sistema de 3 \times 2.

Sistemas Homogêneos

Um sistema é dito homogêneo se todos os seu termos independentes são nulos. Por exemplo: \left\{ \begin{array}{lll} x+2y+z& = & 0\\ x-y -z& = & 0\\ 2x-3y +3z& = & 0\\ \end{array} \right. é um sistema homogêneo. Em um sistema homogêneo com n incógnitas, (0,0,0,0,…,0) é sempre solução do sistema e esta é chamada de solução trivial do sistema. Logo, todo sistema homogêneo é possível ou consistente.

Sistemas Lineares Equivalentes

Seja S um sistema linear de m equações com n incógnitas. Interessa-nos considerar os sistemas que podem ser obtidos de S de uma das seguintes maneiras

1. Permutar duas linhas de S ;
2. Multiplicar uma linha de S por um número diferente de zero;
3. Somar a uma linha S uma outra linha de A multiplicada por um número.

Se um sistema linear S_1 puder ser obtido de S através de um número finito destas operações, diz-se que S_1 é equivalente S e escreve-se S_1  \sim S . Para esta relação valem as propriedades reflexiva (ou seja, S \sim S ), simétrica (ou seja, S \sim S_1  \Leftrightarrow S_1  \sim S )  e transitiva (ou seja, S \sim S_1 , S_1  \sim S_2  \Rightarrow S \sim S_2  ).

Desta forma, criamos um mecanismo extremamente útil para a procura de soluções de um sistema linear S . Como sistemas equivalentes possuem a mesma solução, podemos procurar um sistema linear equivalente a S e que seja “mais simples”, mas precisamente, procuraremos por sistemas escalonados.

Um sistema escalonado é um sistema que possui pelo um coeficiente não nulo em cada equação e o número de coeficientes nulos em cada equação cresce de equação para equação.

EXEMPLO:

1. \left\{ \begin{array}{lll} x+y+z& = & 4\\ y -z& = & 5\\ 3z& = & 3\\ \end{array} \right. É um sistema chamado de escalonado que possui solução igual a (0,3,1); e
2. \left\{ \begin{array}{lll} x+3y-z& = & 4\\ 3y +z& = & 1\\ \end{array} \right. é um sistema escalonado com solução igual a \left(3+2z, \dfrac{1-z}{3}, z \right).

EXEMPLO: Consideremos o sistema $$ \left\{ \begin{array}{lll} x-y+z& = &1 \\ 2x-y+z& = & 4\\ x – 2y + 2z& = & 0\\ \end{array} \right. $$ Para estudar este sistema linear deve-se aplicar a ele uma série de operações elementares visando fazer com que o número de coeficientes iniciais nulos seja maior em cada equação (a a partir da segunda) do que na precedente da seguinte forma:

1. Multiplicamos a primeira equação por -2 e somamos o resultado com a segunda equação: $$ \left\{ \begin{array}{rll} x-y+z& = &1 \\ y-z& = & 2\\ x – 2y + 2z& = & 0\\ \end{array} \right. $$
2. Multiplicamos a primeira equação por -1 e somamos com a terceira: $$ \left\{ \begin{array}{rll} x-y+z& = &1 \\ y-z& = & 2\\ -y + z& = & -1\\ \end{array} \right. $$
3. Somamos a segunda equação com a terceira: $$ \left\{ \begin{array}{rll} x-y+z& = &1 \\ y-z& = & 2\\ 0& = & 1\\ \end{array} \right. $$

Como este último sistema é impossível, podemos concluir que o sistema inicial também é impossível.

Como Resolver Sistemas Lineares Usando Escalonamento?

O problema central da álgebra linear é a solução de equações lineares. O caso mais importante, e o mais simples, se dá quando o número de incógnitas é igual ao número de equações. Existem métodos de solução deste tipo de sistema linear envolvendo matrizes (inversas ou a regra de Cramer), mas até mesmo as fórmulas mais sofisticadas envolvendo determinantes se torna um desastre na prática, principalmente quando se trabalha com quantidades grandes de equações e variáveis; neste caso, o custo computacional é gigantesco.

Até por isso, o escalonamento, ou a Eliminação Gaussiana é um algoritmo constantemente usado para resolver este qualquer tipo de sistema linear e entender este processo é o nosso objetivo a partir de agora. Pode-se provar que todo sistema linear é equivalente a um sistema escalonado. Desta forma, basta que saibamos lidar com os sistemas escalonados e saibamos reduzir um sistema qualquer a um escalonado para usar a eliminação gaussiana. Vamos exemplificar este processo.

Para ilustrar a eliminação gaussiana vamos começar com sistema linear de ordem 3, dado por $$ S = \left\{ \begin{array}{lll}2u+v+w& = & 5 \\ 4u-6v & = & -2\\ -2u+7v+2w& = & 9 \\ \end{array} \right. $$ O método começa subtraindo múltiplos da primeira equação das demais, tal que eliminemos a variável u das demais. Neste caso específico, precisamos:

1. multiplicar a primeira equação por 2 e subtrair da segunda equação;
2. somar a primeira e a terceira equações.

O resultado será o sistema de equações equivalente dado por $$ S = \left\{ \begin{array}{lll}2u+v+w& = & 5 \\ -8v-2w & = & -12\\ 8v+3w & = & 14 \\ \end{array} \right. $$ O coeficiente 2 que multiplica a variável u na primeira equação é conhecido como primeiro pivô. A eliminação se baseia em constantemente dividir o pivô pelo números abaixo dele nas demais equações, para encontrar os multiplicadores certos.

Como segundo passo da eliminação, ignoraremos a primeira equação deste novo sistema e olharemos para as novas segunda e terceira equações. Ambas envolvem apenas as variáveis v e w e a eliminação pode ser aplicada à elas. O pivô neste segundo passo é - 8 , e somando a segunda equação com a terceira obtermos o sistema escalonado $$ S = \left\{ \begin{array}{lll}2u+v+w& = & 5 \\ -8v-2w & = & -12\\ w & = & 2 \\ \end{array} \right. $$

Agora podemos perceber uma ordem óbvia para resolver este sistema linear. A última equação nos dá w = 2. Substituindo na segunda equação, obtemos -8v -4 =-12 , logo v = 1. Por fim, substituindo na primeira equação, temos 2u + 1 +2 = 5, logo u = 1.

Lembrando que estas eliminações progressivas produziram os pivôs 2, -8 e 1.

OBSERVAÇÃO: Por definição os pivôs não podem ser zero uma vez que precisaremos dividir as equações lineares por eles em seus respectivos passos do processo da eliminação gaussiana.

EXEMPLO: Vamos discutir o sistema linear: $$ S = \left\{ \begin{array}{lll} 2x-y+z-t& = & 4 \\ 3x + 2y -z + 2t& = & 1\\ 2x -y – z -t & = & 0\\ 5x +2t & = & 0\\ \end{array} \right. $$

Usando a mesma lógica da aplicação das operações elementares que fizemos no exemplo anterior, podemos encontrar a sequência abaixo de sistemas equivalentes ao sistema S :

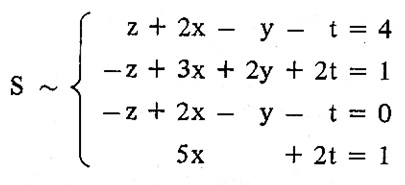
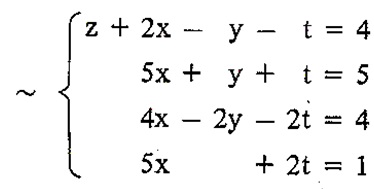
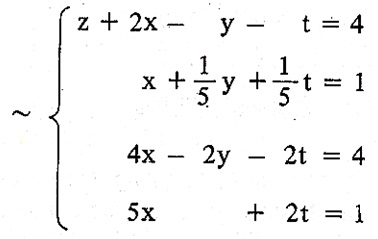
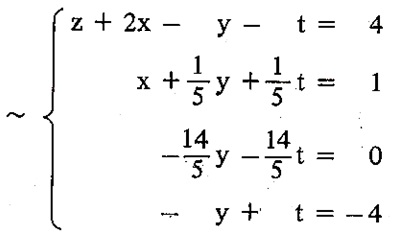
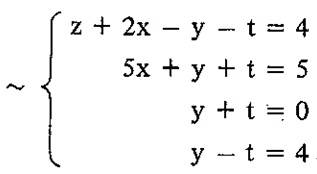
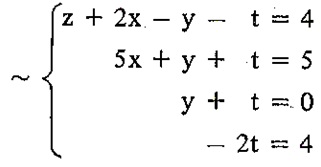
A partir deste sistema escalonado podemos encontrar $$ t = \frac{4}{-2} = -2 $$ $$ y+ (-2) = 0 \Leftrightarrow y = 2$$ $$ 5x+2 -2 = 5 \Leftrightarrow x = 1 $$ $$ z +2 -2 +2 = 4 \Leftrightarrow z = 2 .$$ Portanto, (1,2,2,-2) é a única solução de S , pois é a única solução do sistema escalonado. Portanto, este é um sistema possível e determinado.

EXEMPLO: Vamos discutir e resolver o sistema linear: $$ S = \left\{ \begin{array}{lll}x – 2y – z & = & 1 \\ 2x + y -3z& = & 0\\ x -7y & = & 3\\ \end{array} \right. $$ Através de operações elementares como feitas anteriormente encontramos os seguintes sistemas equivalentes:

Daí, tiramos que $$ S = \left\{ \begin{array}{lll}x & = & \frac{1}{5} + \frac{7}{5} z \\ y& = – \frac{2}{5} + \frac{1}{5} z\\ \end{array} \right. $$ Portanto, este é um sistema possível e indeterminado e seu conjunto solução é dado por $$ \left\{ \left(  \frac{1}{5} + \frac{7}{5} z , – \frac{2}{5} + \frac{1}{5} z , z\right) | z \in \mathbb{R} \right\}. $$

Leia Mais Sobre Matrizes e Sistemas Lineares

• Matrizes – Definições Básicas e Primeiros Exemplos
• Determinante de Matrizes | As Regras de Sarrus, Laplace, Vandermonde e Chió
• Inversão de Matrizes | Como calcular inversa de uma matriz?