Equações Diferencias Ordinárias de 2ª Ordem: Equações Homogêneas

Neste artigo queremos apresentar a teoria clássica para solucionar equações diferenciais homogêneas de segunda ordem Em geral, uma equação diferencial de segunda ordem tem a forma \dfrac{d^2y}{dt^2}=f\left(t,y,\dfrac{dy}{dt} \right), onde f é uma função dada. Uma EDO linear de segunda ordem é dita homogênea se y'' + p(t) y'+q(t) y = 0 ou se P(t)y'' + Q(t) y'+ R(t) y = 0.

Vamos estudar estas equações de segunda ordem lineares, homogêneas e com coeficientes não necessariamente constantes. Se você estiver procurando soluções para este mesmo tipo de EDO, mas com coeficientes contantes, vá para este outro artigo: Equações Diferenciais Ordinárias de 2ª Ordem, Homogêneas, com Coeficientes Constantes

Associamos à equação homogênea um conjunto de condições iniciais dadas por y(t_0) = y_0, y'(t_0)=y'_0, onde t_0 é qualquer ponto no intervalo I, e y_0 e y'_0 são números reais dados.

TEOREMA DA EXISTÊNCIA E UNICIDADE DE SOLUÇÕES

TEOREMA: Considere o problema de valor inicial y''+ p(t)y'+q(t)y = g(t) com y(t_0)=y_0 e y'(t_0)=y'_0, onde p(t),q(t) e g(t) são contínuas em um intervalo aberto I. Então, existe exatamente uma solução y=\phi (t) desse problema, e a solução existe em todo o intervalo I.

Uma demonstração deste teorema pode ser encontrada nesse livro. Para exemplificar vamos encontrar o maior intervalo no qual a solução do problema de valor inicial \left( t^2 - 3t \right) y''+ ty' - (t+3)y = 0; \;\;\;y(1)=2; \;\;\; y'(1)=1 certamente existe.

Temos que \left( t^2 - 3t \right) y''+ ty' - (t+3)y = 0 \Rightarrow y'' + \dfrac{t}{\left( t^2 - 3t \right)}y' - \dfrac{(t+3)}{\left( t^2 - 3t \right)} = 0\Rightarrow \Rightarrow y'' + \dfrac{1}{\left( t - 3 \right)}y' - \dfrac{(t+3)}{t \left( t - 3 \right)}=0 cujos únicos pontos de descontinuidade são os pontos t=0 e t=3.

Logo, o maior intervalo, contendo o ponto inicial t=1, no qual todos os coeficientes são contínuos é 0<t<3. Portanto, neste intervalo o teorema acima garante a existência e a unicidade da solução da PVI dado.

WRONSKIANO E A SOLUÇÃO GERAL DA EQUAÇÃO HOMOGÊNEA

Vamos supor que y_1 e y_2 sejam duas soluções da equação y'' + p(t) y' + q(t)y=0 então a combinação linear c_1 y_1 +c_2y_2 também é solução, quaisquer que sejam os valores das constantes c_1 e c_2.

Ou seja, dadas duas soluções y_1 e y_2 de y'' + p(t) y' + q(t)y=0, y(t) = c_1 y_1 (t) +c_2y_2 (t) é, também, solução da equação.

Uma pergunta a ser respondida é se esta solução y(t) é a solução geral de y'' + p(t) y' + q(t)y=0. Para responder a esta questão precisamos da definição de um determinante conhecido como determinante Wronskiano ou apenas wronskiano das soluções y_1 e y_2 que é dado por

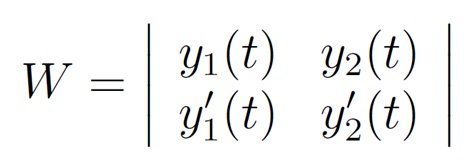
EXEMPLO: Considere a EDO y''+5y'+6y = 0.

Sabemos que sua solução geral é dada por y(t) = c_1 e^{-2t} + c_2 e^{-3t}.

Podemos perceber facilmente que y_1(t)=e^{-2t}\;\;\;e\;\;\;y_2(t)= e^{-3t} são soluções particulares da EDO acima.

Logo, o wronskiano é dado por

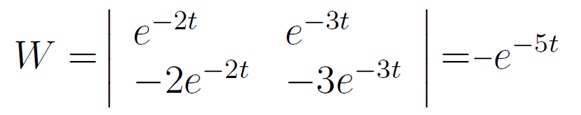
Se y_1 e y_2 são duas soluções da equação diferencial y'' + p(t) y' + q(t)y=0 e se existe um ponto t_0 onde o wronskiano de y_1 e y_2 é diferente de zero, então a família de soluções y(t) = c_1 y1(t) + c_2 y_2(t) com coeficientes arbitrários c_1 e c_2 inclui todas as soluções da equação diferencial original.

As soluções y_1 e y_2 de y'' + p(t) y' + q(t)y=0, com wronskiano não-nulo, formam um conjunto fundamental de soluções da equação diferencial.

EXEMPLO: Mostre que y_1(t) = \sqrt{t} e y_2 (t)= \dfrac{1}{t} formam um conjunto fundamental de soluções da equação 2t^2 y'' + 3t y' -y = 0, \;\;\;\;t>0.

Primeiro, vamos verificar se estas funções são, realmente, soluções da EDO dada:

y'_1(t) = \dfrac{1}{2} t^{-1/2} e y''_1(t) = \dfrac{-1}{4} t^{-3/2}. Daí, 2t^2 y'' + 3t y' -y = 2t^2 \dfrac{-1}{4} t^{-3/2} + 3t \dfrac{1}{2} t^{-1/2}- \dfrac{1}{2} t^{-1/2} = = \left( \dfrac{-1}{2} + \dfrac{3}{2} - 1 \right) t^{-1/2} = 0.

y'_2(t) = -t^{-2} e y''_1(t) = 2t^{-3}. Daí, 2t^2 y'' + 3t y' -y = 2t^2 2t^{-3} + 3t \-t^{-2} - \dfrac{1}{t} = \left( 4-3 - 1 \right) t^{-1} = 0.

A seguir vamos calcular o wronskiano de y_1 e y_2:

com W\neq 0 para t>0, concluímos que y_1 e y_2 formam um conjunto fundamental de soluções.

EXEMPLO: Encontre um conjunto fundamental de soluções para a equação diferencial y'' - y = 0.

Para encontrar este conjunto fundamental de soluções basta estabelecer, num primeiro momento, que y(0) = 1 e y'(0)=0. Daí,

y_1(t) = \frac{1}{2}e^{t}+\frac{1}{2}e^{-t}=cosh(t). Num segundo momento, fazemos y(0) = 0 e y'(0)=1 e obtemos y_2(t) = \frac{1}{2}e^{t}+\frac{1}{2}e^{-t}=senh(t).Daí o wronskiano é dado por W = cosh^2(t) - senh^2(t) = 1

 Portanto, \{ cosh(t), senh(t) \} é um conjunto fundamental de soluções para a EDO y'' - y = 0.

O TEOREMA DE ABEL

Vamos examinar alguas propriedades do wronskiano de duas soluções de uma EDO de segunda ordem homogênea. O próximo teorema consegue explicitar a forma do wronskiano de quaisquer duas funções de uma EDO específica, mesmo de suas soluções não forem conhecidas.

[Teorema de Abel] Se y_1 e y_2 são duas soluções da EDO y'' + p(t) y' + q(t)y=0, onde p(t), q(t) são contínuas em um intervalo aberto I, então o Wronskiano é dado por W\left( y_1, y_2 \right) (t) = c e^{-\int p(t)dt}, onde c é uma constante que irá ser determinada pela funções y_1 e y_2. Portanto, W\left( (y_1, y_2 \right) (t) será zero somente se c=0.

EXEMPLO: Considere novamente a EDO 2t^2 y'' + 3t y' -y = 0, \;\;\;\;t>0. Sabemos que W\left( y_1, y_2 \right) (t) = -\dfrac{3}{2}t^{-3/2 t}, para o conjunto fundamental de soluções y_1(t) = \sqrt{t} e y_2 (t)= \dfrac{1}{t}. Vamos testar a fórmula de Abel. Temos que y'' + \dfrac{3}{2t} y' -\dfrac{1}{2t^2}y = 0, \;\;\;\;t>0, ou seja, p(t) = \dfrac{3}{2t}. Portanto, W\left( y_1, y_2 \right) (t) = c e^{-\int {\frac{3}{2t} dt}}= c e^{- \frac{3}{2} ln{t}} = c t^{-3/2}. No caso das soluções particulares dadas, a constante c tem valor igual a -3/2.

LISTA DE EXERCÍCIOS RESOLVIDOS SOBRE EDO’S DE 2ª ORDEM HOMOGÊNEAS

• E.D.O.’s Homogêneas de 2ª Ordem | 1ª Lista de Exercícios Resolvidos
• E.D.O.’s Homogêneas de 2ª Ordem | 2ª Lista de Exercícios Resolvidos

LEIA MAIS:

• Equações Diferenciais Ordinárias de 2ª Ordem, Homogêneas, com Coeficientes Constantes
• VARIAÇÃO DOS PARÂMETROS: EDOs de 2ª Ordem Linares
• Equações Diferencias Ordinárias de 2ª Ordem: Método dos Coeficientes Indeterminados
• Equações Diferencias Ordinárias de 2ª Ordem: O Princípio da Superposição
• Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos

Assista Nossa Vídeo-Aula