O que são Curvas e Superfícies de Nível?

As curvas e as superfícies de nível são formas de se visualizar funções de várias variáveis usando representações em dimensões inferiores. Este é um método semelhante ao da representação de uma paisagem tridimensional por meio de um mapa topográfico bidimensional.

As curvas de nível além de utilizadas na elaboração de mapas topográfico ou mapas de contorno, também são importantes na representação de curvas isotérmicas (temperatura constante), curvas isobáricas (pressão constante), etc.

A partir da visualização de uma curva de nível é possível identificar se o relevo de uma determinada área é acidentado, plano, montanhoso, íngreme e etc. Diante dessa afirmação, percebe-se que a configuração das linhas são determinadas pelas características do relevo da área mapeada.

Neste artigo queremos estudar matematicamente as curvas e as superfícies de nível como formas de estudar graficamente as funções de várias variáveis, ou campos escalares.

As Curvas de Nível

Outro modo muito conveniente de visualizar geometricamente uma função de duas variáveis consiste em representar, no plano x0y, as chamadas curvas de nível dessa função.

Neste artifício, atribuímos valores para a variável z, onde z = f(x,y) e o conjunto de pontos (x,y) que satisfazem a equação k = f(x,y) formam, em geral, uma curva C_k , que é chamada de curva de nível da função f correspondente ao valor z=k.

Quando consideramos várias curvas de nível de uma dada função f, podemos formar uma ideia da superfície que é o gráfico dessa função.

DEFINIÇÃO (Curvas de Nível)

Seja k um número real. Uma curva de nível, C_k de uma função z=f(x,y) é o conjunto de todos os pontos (x,y) \in D_f, tais que f(x,y)=k. Simbolicamente, $$C_k = \left\{(x,y) \in D_f ; f(x,y) = k \right\}.$$

EXEMPLO

Para a função z=\sqrt{4-x^2-y^2}, algumas curvas de nível são

$$C_0 : 0=\sqrt{4-x^2-y^2} \Rightarrow x^2+y^2 = 4$$

$$C_1 : 1=\sqrt{4-x^2-y^2} \Rightarrow x^2+y^2 = 3$$

Para k=2, a curva de nível é dada por x^2+y^2 = 0 \Leftrightarrow x=y=0.

EXEMPLO

Seja f dada por $$z=\frac{1}{x^2+y^2}.$$

a) Determine o domínio e a imagem.

O domínio é dado por:

D_f = \left\{ (x,y) \in \mathbb{R} ^2 ; x^2+y^2\neq 0 \right\} = \left\{ (x,y) \in \mathbb{R} ^2 ; x \neq 0 \;\;\;e\;\;\; y\neq 0 \right\} = D_f = \left\{ (x,y) \in \mathbb{R} ^2 ; (x,y) \neq (0,0) \right\}

Já a imagem é dada por

Im_f = \left\{ z \in \mathbb{R}; z=\dfrac{1}{x^2+y^2} >0 \right\}

b) Esboce as curvas de nível.

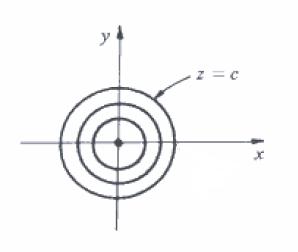
Queremos constantes c \in \mathbb{R}, tais que $$c=\frac{1}{x^2+y^2} \Leftrightarrow x^2+y^2 = \frac{1}{c}.$$ As curvas de nível são círculos concêntricos de centro na origem (0,0). Quando c tende a + \infty, o raio tende a zero, quando c tende a 0, o raio tende a + \infty.

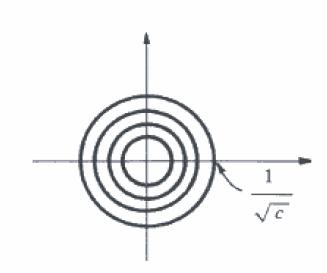
c) Esboce o gráfico

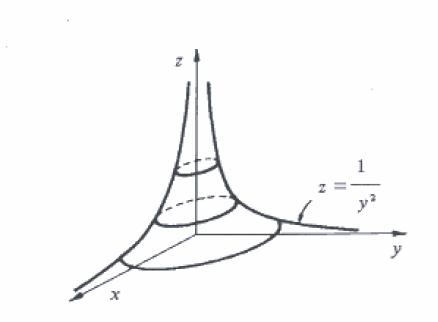
Para x=0 encontramos a curva z=\dfrac{1}{y^2}. Como as curvas de nível de f são circunferências concêntricas, basta girarmos esta curva em torno do eixo z. Assim,

EXEMPLO:

Seja f(x,y) = \dfrac{2xy^2}{x^2 + y^4}, \;\;\; (x,y) \neq (0,0)

Vamos esboçar as curvas de nível desta função

Se c = 0, então f(x,y) = \dfrac{2xy^2}{x^2 + y^4} = 0 \Leftrightarrow x=0, \;\;\;ou\;\;\; y=0

Para c \neq 0 , então f(x,y) = \dfrac{2xy^2}{x^2 + y^4} = c \Leftrightarrow x = \dfrac{1 \pm \sqrt{1 - c^2}}{c} y^2 \;\;\; (-1 \leq c \leq 1, c \neq 0).

Ou seja, as curvas de nível neste caso são parábolas, na forma $$ x = k y^2 ,$$ onde $$k = \frac{1 \pm \sqrt{1 – c^2}}{c},$$ e excluindo delas o ponto (0,0), pois (x,y) \neq (0,0) .

As curvas de nível neste caso são dadas pelas parábolas da figura abaixo:

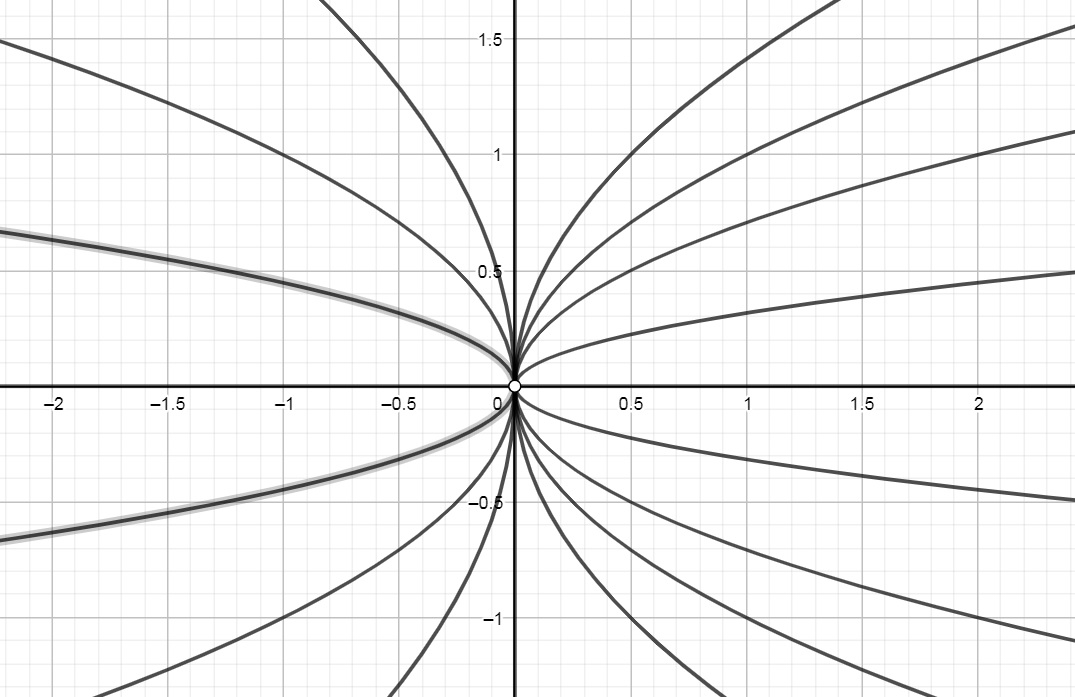
Nesta figura, à medida que c vai se aproximando de zero, a parábola definida por x = \dfrac{1 - \sqrt{1 - c^2}}{c} y^2 vai se “abrindo” cada vez mais , enquanto x = \dfrac{1 + \sqrt{1 - c^2}}{c} y^2 vai “fechando” cada vez mais.

Abaixo, apresentamos o gráfico de f(x,y) = \dfrac{2xy^2}{x^2 + y^4}, \;\;\; (x,y) \neq (0,0) :

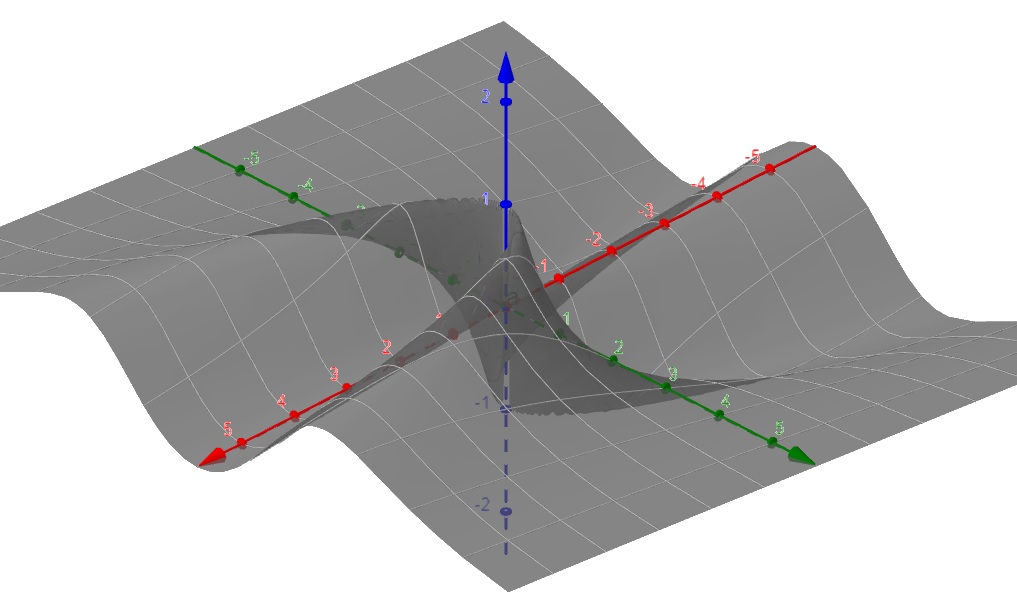
Superfícies de Nível

Seja w=f(x,y,z), com (x,y,z) \in A \subset \mathbb{R} ^n, uma função real de três variáveis reais. O conjunto $$G_f=\left\{ (x,y,z,w) \in \mathbb{R} ^4 / w=f(x,y,z),\;\;\; (x,y,z) \in A \right\}$$ denomina-se gráfico de f. Seja k um número real. Uma curva de nível, C_k de uma função w=f(x,y,z) é o conjunto de todos os pontos (x,y,z) \in D_f, tais que f(x,y,z)=w. Simbolicamente, $$C_k = \left\{(x,y,z) \in D_f ; f(x,y,z) = k \right\}.$$

EXEMPLO

Determinar as superfícies de nível da função w=x^2+y^2+z^2. Dar exemplos de três pontos pertencentes ao gráfico de w.

As superfícies de nível da função w são dadas por $$S_k = \left\{ (x,y,z) \in \mathbb{R} ^3 ; x^2+y^2+z^2 = k \right\},$$ que são esferas de raio r=\sqrt{k}. Assim,

i)  k=0 \Rightarrow x=y=z=0.

ii)  Se k<0 então S_k é um conjunto vazio.

iii) O gráfico de w é o conjunto $$G_{w} = \left\{ (x,y,z,w) \in \mathbb{R}^4 / w=x^2+y^2+z^2 \right\} $$ e alguns pontos que pertencem a este conjunto são P_{1} (1,2,1,6), P_{2} (0, -1,2,5) e P_{1} (-2,-3,1,14)

Leia Mais:

• Funções de Várias Variáveis | Domínio, Imagem e Gráfico
• Vetor Gradiente | Definição, Campo Gradiente e Exercícios Resolvidos
• Limite e Continuidade de Funções de Várias Variáveis Reais