Curvas no Espaço | 5ª Lista de Exercícios Resolvidos

Uma curva parametrizada é a imagem de uma função de uma variável a valores no \mathbb{R}^n. Assim, uma função $$f(t)=(x_1(t), x_2(t),…,x_n(t))\;\;\;\;t\in \mathbb{R}$$ é uma curva e as funções reais x_i(t),\; i=1,...,n, são as equações paramétricas da curva e t é chamado de parâmetro.

Porém, com mais acuidade matemática definimos como curva o conjunto de todos os pontos (x(t), y(t), z(t)) do espaço determinados por uma função vetorial de uma variável.

Nesse artigo queremos apresentar uma terceira lista de exercícios resolvidos sobre o tema.

Curvas no Espaço | 5ª Lista Exercícios Resolvidos

1) Encontre a parametrização de cada uma das curvas abaixo:

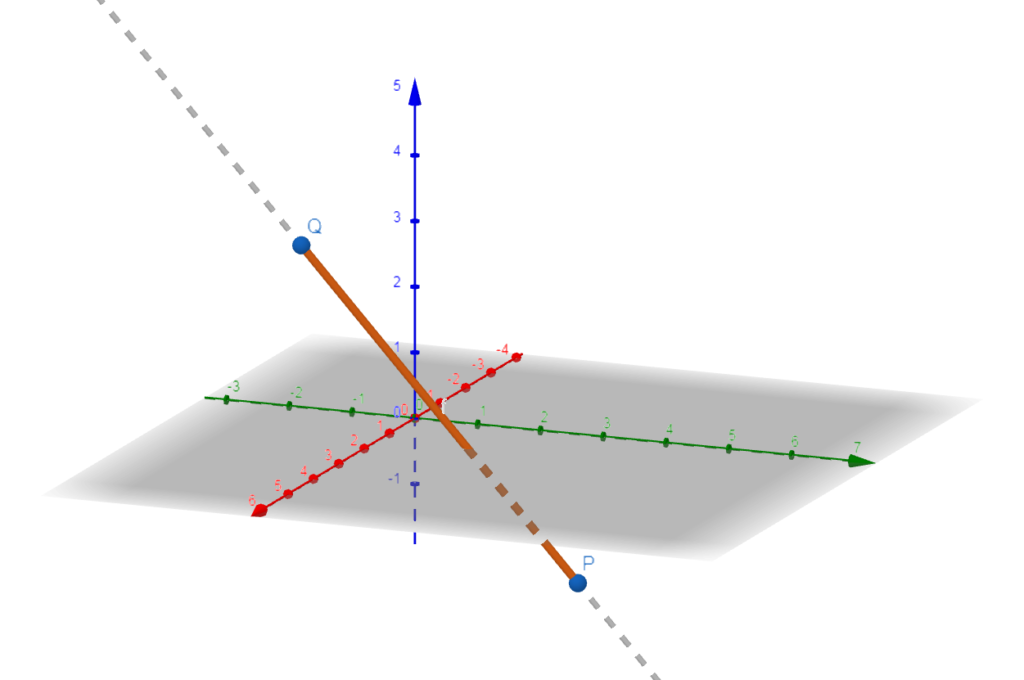
a) \vec{r} (t) é o segmento de reta que se inicia no ponto P(1,3,-2) e termina Q(2,-1,3);

SOLUÇÃO: Observe que neste caso, o vetor diretor da reta suporte deste segmento é dado por \vec{PQ} = \left( 2-1, -1 -3, 3 - (-2) \right) = (1, -4, 5) . Com isso, as equações paramétricas desta reta suporte serão dadas por $$ r:\left\{ \begin{array}{lll} x & = & 1 + t\\ y & = & 3\; – 4 t\\ z & = & -2 + 5t \end{array} \right. \qquad t \in \mathbb{R} $$

Agora, precisamos saber para quais valores de t atingimos os pontos P e Q. Facilmente, percebemos que quando t = 0 atingimos o ponto P, e quando t = 1 atingimos o ponto Q.

Portanto, a parametrização do segmento que se inicia no ponto P(1,3,-2) e termina Q(2,-1,3) é dada por $$ \overline{PQ}:\left\{ \begin{array}{lll} x & = & 1 + t\\ y & = & 3\; – 4 t\\ z & = & -2 + 5t \end{array} \right. ;\qquad t \in [0,1].$$

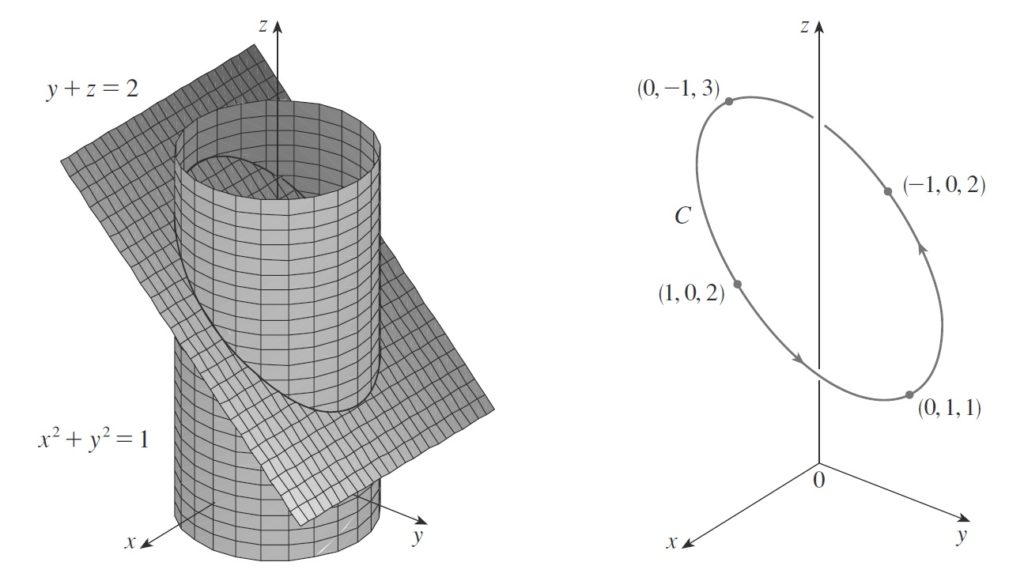
b) \vec{f} (t) é a curva interseção do cilindro x^2+y^2 = 1 e do plano y+z = 2.

SOLUÇÃO: Observe que a equação do plano pode ser reescrita como y = 2 - z. Logo, a interseção do plano e do cilindro tem que satisfazer a equação $$x^2 + (2-z)^2 = 1 \Leftrightarrow  x^2 + (z-2)^2 = 1 $$ que é uma elipse centrada no ponto (0, 0 , 2) e com raios maior e menor igual a 1.

Neste caso, pela parametrização da elipse (dada neste artigo) encontramos $$x(t) = cos(t)$$ $$z(t) = 2 – sen(t) .$$ Falta encontrar y(t) . Para isso, usaremos a equação do plano: $$y+z = 2 \Leftrightarrow y = 2 -z = 2- (2 – sen(t) ) = sen(t) .$$

Portanto, a interseção do x^2+y^2 = 1 e do plano y+z = 2 é uma elipse dada pela parametrização $$ \vec{f} (t) = \left\{ \begin{array}{lll} x & = & cos(t) \\ y & = & sen(t) \\ z & = & 2 – sen(t) \end{array} \right. ;\qquad t \in [0,2 \pi]$$ e representada graficamente pela figura abaixo:

2) Reparametrize pelo comprimento de arco a hélice $$ \vec{\gamma} (t) = (cos(t), sen(t), t)$$ partindo do ponto (1,0,0) e na direção crescente de t.

SOLUÇÃO: O ponto inicial (1,0,0) corresponde ao valor de parâmetro t = 0. Observe que $$ | \gamma ‘ (t) | = \sqrt{[-sen(t)]^2 + [cos(t)]^2 +1} = \sqrt{2} .$$ Logo, o comprimento de arco da hélice partindo do ponto (1,0,0) e na direção crescente de t é dado por $$s(t) = \int_{0}^{t}{\sqrt{2} du} = \sqrt{2} t .$$

Portanto, $$ s = \sqrt{2} t \Leftrightarrow t = \frac{s}{\sqrt{2}} $$ e a reparametrização pedida é obtida pela substituição t = \dfrac{s}{\sqrt{2}} : $$ \vec{\gamma} (s) = cos \left( \frac{s}{\sqrt{2}} \right) \vec{i} + sen\left( \frac{s}{\sqrt{2}} \right) \vec{j} + \frac{s}{\sqrt{2}} \vec{k} .$$

3) Encontre o comprimento de arco de cada uma das curvas abaixo:

a) \vec{f} (t) = 2 sen(t) \; \vec{i} + 5t\vec{j} + 2cos(t)\; \vec{k}; -10 \leq t \leq 10.

SOLUÇÃO: Como $$ \vec{f} ‘ (t) = \left( 2 cos(t), 5 , -2 sen(t) \right) \Leftrightarrow | \vec{f} ‘ (t) | = \sqrt{4 cos^2 (t) + 25 + 4 sen^2 (t)} = \sqrt{29}$$ usamos a fórmula do comprimento do arco e encontramos $$ s = \int_{-10}^{10}{ | \vec{f} ‘ (t) | dt} = \int_{-10}^{10}{ \sqrt{29} dt} = 20 \sqrt{29} . $$

b) \vec{f} (t) = \left( 1 , t^2 , t^3 \right); 0 \leq t \leq 1.

SOLUÇÃO: Como $$ \vec{f} ‘ (t) = \left( 0, 2t , 3t^2 \right) \Leftrightarrow | \vec{f} ‘ (t) | = \sqrt{4t^2 + 9t^4} = t \sqrt{4+9t^2}$$ usamos a fórmula do comprimento do arco e encontramos $$ s = \int_{0}^{1}{ | \vec{f} ‘ (t) | dt} = \int_{0}^{1}{ t \sqrt{4+9t^2} dt} = \left[ \frac{1}{27} \left( 4+9t^2 \right)^{3/2} \right]_{0}^{1} = \frac{1}{27} \left( 13^{3/2} – 8 \right) .$$

3) Encontre a velocidade, a aceleração e a velocidade escalar da partícula com posição dada por \vec{r} (t) = (t^2, e^t , t e^t).

SOLUÇÃO: $$\vec{v} (t) = \vec{r} ‘ (t) = \left( 2t, e^t , (1+t) e^t \right) $$ $$ \vec{a} (t) = \vec{v}'(t) = \left( t, e^t , (2+t) e^t \right) $$ $$ | \vec{v} (t) | = \sqrt{4t^2 + e^{2t} + (1 +t)^2 e^{2t}}$$

 4) Uma partícula se move partindo da posição inicial \vec{r} (0) = (1,0,0) e com velocidade inicial dada por \vec{v}(0) = (1,-1,1). Sua aceleração é \vec{a} (t) = (4t, 6t, 1). Determine sua posição e sua velocidade no tempo t.

SOLUÇÃO: Desde que \vec{a} (t) = \vec{v} ' (t) , nós temos $$ \vec{v} (t) = \int{\vec{a} (t) dt} = \int{(4t\vec{i} + 6t \vec{j} + \vec{k})dt } = 2t^2\vec{i} + 3t^2 \vec{j} + t \vec{k} + \vec{C}.$$

Para determinar o valor do vetor constante \vec{C} , usamos o fato de que \vec{v} (0) = (1,-1,1) . Como

$$ \vec{v} (0) = 2\times 0^2\vec{i} + 3\times 0^2 \vec{j} + 0 \times \vec{k} + \vec{C} = (1,-1,1) \Leftrightarrow \vec{C} = (1,-1,1)$$ Portanto,  $$ \vec{v} (t) = (2t^2 +1) \vec{i} + (3t^2 -1) \vec{j} + (t + 1) \vec{k}.$$

Agora, como \vec{v} (t) = \vec{r} ' (t) , nós temos $$ \vec{r} (t) = \int{ \vec{v} (t) dt} = \left( \frac{2}{3} t^3 +t \right) \vec{i} + \left( t^3 – t \right) \vec{j} + \left( \frac{1}{2} t^2 +t \right) \vec{k} + \vec{D}$$

Fazendo t = 0 , encontramos \vec{D} = \vec{r} (0) = \vec{i} , portanto $$ \vec{r} (t) = \left( \frac{2}{3} t^3 +t +1 \right) \vec{i} + \left( t^3 – t \right) \vec{j} + \left( \frac{1}{2} t^2 +t \right) \vec{k}.$$

Leia Mais:

• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Curvas no Espaço | 2ª Lista de Exercícios Resolvidos
• Curvas no Espaço | 1ª Lista de Exercícios Resolvidos
• Curvas no Espaço | 3ª Lista de Exercícios Resolvidos
• Curvas no Espaço | 4ª Lista de Exercícios Resolvidos

Assista nossa video-aula com alguns destes exercícios resolvidos: