Curvas no Espaço | 2ª Lista de Exercícios Resolvidos

Uma curva parametrizada é a imagem de uma função de uma variável a valores no \mathbb{R}^n. Assim, uma função $$f(t)=(x_1(t), x_2(t),…,x_n(t))\;\;\;\;t\in \mathbb{R}$$ é uma curva e as funções reais x_i(t),\; i=1,...,n, são as equações paramétricas da curva e t é chamado de parâmetro.

Porém, com mais acuidade matemática definimos como curva o conjunto de todos os pontos (x(t), y(t), z(t)) do espaço determinados por uma função vetorial de uma variável.

Nesse artigo queremos apresentar uma segunda lista de exercícios resolvidos sobre o tema.

Curvas no Espaço | 2ª Lista Exercícios Resolvidos

1) Seja F(t) = \dfrac{\vec{u} + 2 \vec{v}}{t-2}, onde \vec{u} = \vec{i} e \vec{v} = 2 \vec{j} - \vec{k}. Calcular:

a) \lim_{t \rightarrow 0}{F(t)} ;

b) \lim_{t \rightarrow 2}{(t^2 - 4t +4) F(t)} ;

SOLUÇÃO: Antes de resolver os itens, observe que nas condições do enunciado F(t) = \dfrac{\vec{u} + 2 \vec{v}}{t-2} = \dfrac{1}{t-2} (1,4,-2).

Assim,

a) \lim_{t \rightarrow 0}{F(t)} = \lim_{t \rightarrow 0}{\dfrac{1}{t-2} (1,4,-2)} = -\dfrac{1}{2} (1,4,-2) = \left( -\dfrac{1}{2} , -2, 1 \right) . ;

b) \lim_{t \rightarrow 2}{(t^2 - 4t +4) F(t)}  = \lim_{t \rightarrow 2}{(t^2 - 4t +4) \dfrac{1}{t-2} (1,4,-2)} =  \lim_{t \rightarrow 2}{(t-2)^2 \dfrac{1}{t-2} (1,4,-2)} =  \lim_{t \rightarrow 2}{(t-2)(1,4,-2)} = (0,0,0) ;

2) Indique o intervalo de continuidade de $$F(t) = \left( e^t , \frac{t^2 – 1}{t-1}, \ln{(t+1)} \right).$$

SOLUÇÃO: Os intervalos de continuidade das funções componentes são dados abaixo:

1. Domínio de e^t : \mathbb{R} ;
2. Domínio de \dfrac{t^2 - 1}{t-1} : \mathbb{R} - \{0\} ;
3. Domínio de \ln{(t+1)}  : \{t \in \mathbb{R} / t >0 \} .

Portanto, a interseção destes domínios, dado por \{t \in \mathbb{R} / t >0 \} , é o intervalo de continuidade de F(t) .

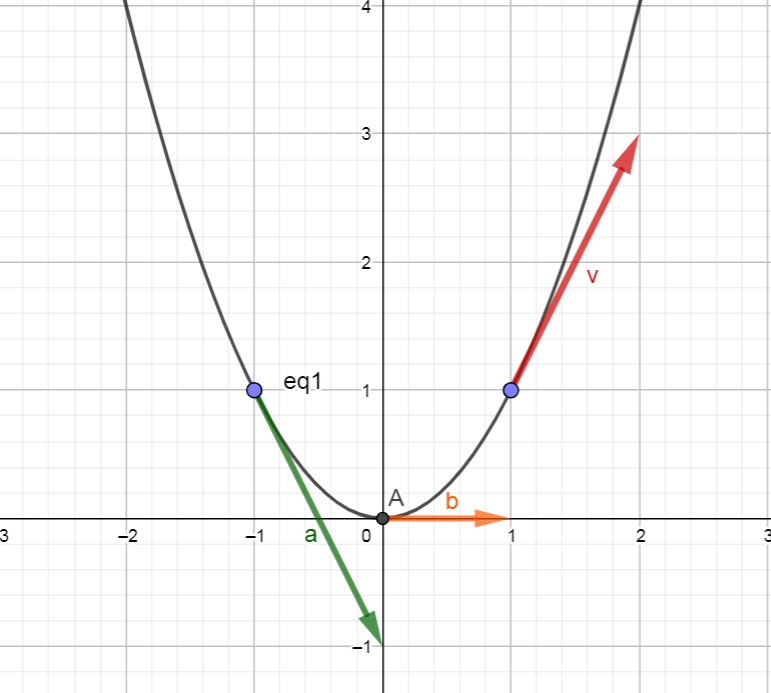
3) Dada F(t) = (t, t^2) , determine F'(t) . Esboce a trajetória dessa função vetorial e nele esboce os vetores F'(1) , F'(-1) e F'(0) .

SOLUÇÃO: Primeiramente, F'(t) = (1, 2t) . No esboço abaixo, temos a trajetória da parábola determinada pela função e os vetores F'(1) = (1,2) , F'(-1) = (1,-2) e F'(0) = (1,0) , respectivamente, nas cores vermelho, verde e laranja.

4) Seja F(t) = (cost, sent). Mostre que F'(t) é ortogonal a F(t) .

SOLUÇÃO: Como F'(t) = (- sen(t), cos(t)), então $$F(t) . F’ (t) = (- sen(t), cos(t)) . (cost, sent) = -sen(t) cos(t) +cos(t) sen(t) = 0,$$ ou seja, usando o produto vetorial mostramos que F'(t) é ortogonal a F(t) .

5) Calcule o comprimento da elipse com eixos com medidas a,b>0 sobre os eixos coordenados e centrada na origem.

SOLUÇÃO: Como a parametrização da elipse $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ é dada por $$ \gamma (t) = (a cos(t), b sen(t)),$$ então o comprimento de arco dessa elipse é dada por $$ s(t) = \int_{0}^{2 \pi}{\sqrt{a^2 sen^2 (t) + b^2 cos^2 (t)} dt}.$$

6) Uma partícula se desloca no espaço. Em cada instante t o seu vetor posição é dado por $$\vec{r} (t) = \left(t, \frac{t}{t-2},1 \right).$$

a) Determinar a posição da partícula nos intantes t=0 e t=1.

SOLUÇÃO:  \vec{r} (0) = \left(0, 0,1 \right) e \vec{r} (0) = \left(1, -1 ,1 \right). winplo

b) Esboce a trajetória desta partícula

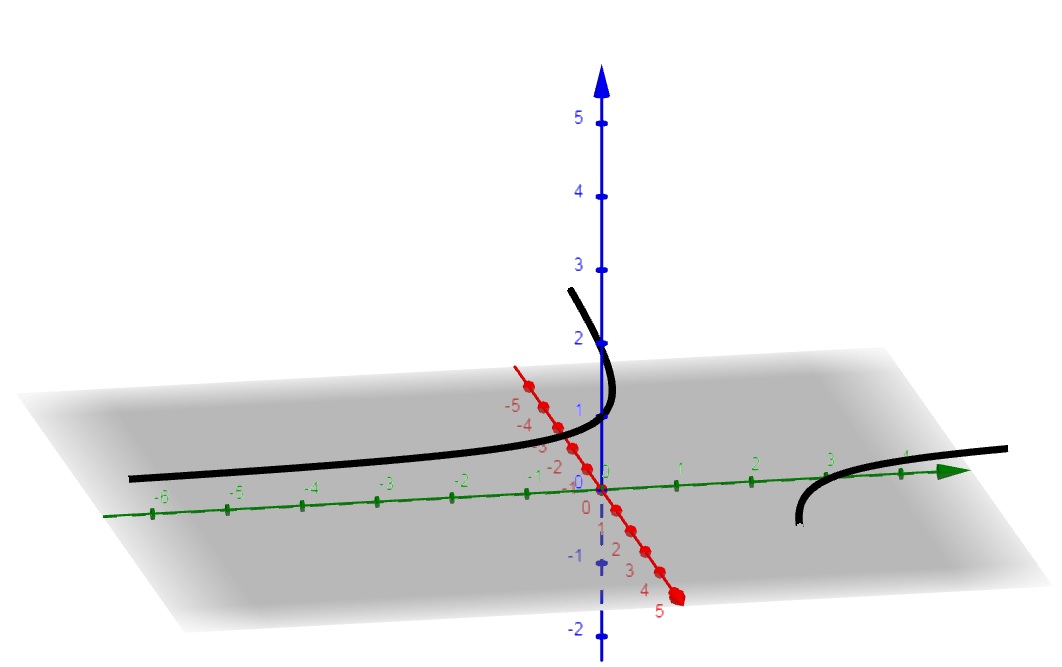
c) Quando t se aproxima de 2 o que ocorre com a posição da partícula?

SOLUÇÃO: $$ \lim\limits_{t \rightarrow 2}{\vec{r} (t)} = \left( \lim\limits_{t \rightarrow 2}{t}, \lim\limits_{t \rightarrow 2}{\frac{t}{t-2}}, \lim\limits_{t \rightarrow 2}{1}\right) = \left(2, \lim\limits_{t \rightarrow 2}{\frac{t}{t-2}}, 1\right).$$ Como \lim\limits_{t \rightarrow 2}{\frac{t}{t-2}} = \infty podemos dizer que a posição da partícula se aproxima, paralelamente ao eixo y, da assíntota r: x=2, \;\;\; z=1. em duas direções .

d) Determinar o vetor velocidade e o vetor aceleração em um instante t qualquer.

SOLUÇÃO:  $$\vec{v}(t) = \left( 1, \frac{-2}{(t-2)^2}, 0  \right)$$ $$\vec{a}(t) = \left( 0, \frac{4}{(t-2)^3}, 0  \right).$$

7) Identifique a curva x^2 -8y+4=0 e escreva sua parametrização.

SOLUÇÃO: Ajustando a equação para $$y = \frac{x^2}{8} + \frac{1}{2}$$ percebemos que temos uma parábola, que pode ser parametrizada como $$ \gamma (t) = \left( t, \frac{t^2}{8} + \frac{1}{2}  \right).$$

8) Determine a equação da reta tangente à curva \vec{r}(t)=(cos(t), sen(t), t^2) no ponto t_0 = \frac{\pi}{2}.

SOLUÇÃO: A equação da reta tangente é dada por $$ x= -t$$ $$y = 1$$ $$z = \frac{ \pi ^2}{4} + \pi t$$

9) Encontre a função comprimento da hélice circular $$\vec{r}(t) = (2cos(t), 2sen(t), t).$$

SOLUÇÃO: $$s(t) = \int\limits_{a}^{t}{\sqrt{(-2sen(t))^2 +(2 cos(t))^2 + 1^2} dt} = \int\limits_{a}^{t}{\sqrt{5}dt} = \sqrt{5} (t-a) $$

10) Escreva a parametrização da curva dada pela interseção das superfícies x+y=2 e x^2+y^2+z^2 = 4.

A interseção das superfícies x+y=2 e x^2+y^2+z^2 = 4 é dada pela curva de equação $$\frac{(y-1)^2}{1}+\frac{z^2}{2} = 1,$$ ou seja, a elipse centrada em (0,1,0), sobre o plano yOz e com eixo maior sobre eixo y:

$$\gamma (t) = (0, 1+cos(t), \sqrt{2} sen(t)).$$

11) Escreva a função comprimento de arco da hipocicloide $$\vec{r} (t) = a cos^3 (t) \vec{i} + a sen^3 (t) \vec{j} , \;\;\; t \in \left[0, \frac{\pi}{2} \right]. $$

SOLUÇÃO: $$s(t) = \int\limits_{0}^{x}{9a^2 (cos^2(t)sen^2(t)+sen^4(t)cos^2(t))dt} = \frac{9 a^2 \pi}{16} \left( 4t – sen(4t) \right) .$$

12) Calcule o limite e analise a continuidade das funções vetoriais dadas, nos pontos indicados:

a) f(t) = \left( t, \dfrac{\sqrt{t+2} - \sqrt{2}}{t} \right)  , se t \neq 0 , e f(0) = (0, \sqrt{2}) ; em t = 0 .

SOLUÇÃO: Neste caso podemos ver facilmente que $$ \lim\limits_{t \rightarrow 0}{f(t)} = \left( \lim\limits_{t \rightarrow 0}{t}, \lim\limits_{t \rightarrow 0}{\frac{\sqrt{t+2} – \sqrt{2}}{t}} \right) = (0, \frac{1}{2\sqrt{2}}) \neq f(0).$$ Portanto, a função é descontínua em t = 0 .

b) f(t) = \left( \dfrac{2}{t-1}, \dfrac{4}{t-2}, -5 \right)  , se t \neq 1 e t \neq 2 e f(1) = f(2) = (0, 0 , 0) ; em t = 1 e t = 2.

SOLUÇÃO: Usando técnicas de solução de cálculo de limite podemos perceber que ambos os limites, tanto em t = 1 e em t = 2 , para f(t) os limites das funções componentes x(t) e y(t) não existem. Logo a função não pode ser contínua nestes pontos.

Leia Mais:

• Curvas no Espaço | Funções de uma Variável Real a Valores Vetoriais
• Curvas | Limite e Continuidade de uma Função Vetorial
• Curvas | A Derivada de Funções Vetoriais
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula

Assista nossa Video-Aula com Exercícios Resolvidos: