Nesse artigo queremos apresentar uma quarta lista de exercícios resolvidos envolvendo derivadas, integrais, limites e continuidade das funções vetoriais cujas imagens são curvas no espaço. Uma curva parametrizada é a imagem de uma função de uma variável a valores no \mathbb{R}^n. Assim, uma função $$f(t)=(x_1(t), x_2(t),…,x_n(t))\;\;\;\;t\in \mathbb{R}$$ é uma curva e as funções reais x_i(t),\; i=1,...,n, são as equações paramétricas da curva e t é chamado de parâmetro.
Curvas no Espaço | 4ª Lista de Exercícios Resolvidos
1) Calcule os limites abaixo:
a) \lim_{t \rightarrow 1}{\vec{F}(t)} , onde \vec{F}(t) = \left( \dfrac{\sqrt{t} -1}{t-1} , t^2 , \dfrac{t-1}{t} \right)
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
SOLUÇÃO: Observe que teremos uma indeterminação apenas na primeira função componente: $$ \lim_{t \rightarrow 1}{\vec{F}(t)} = \lim_{t \rightarrow 1}{\left( \frac{\sqrt{t} -1}{t-1} , t^2 , \frac{t-1}{t} \right)} = $$ $$ = \left( \lim_{t \rightarrow 1}{\frac{\sqrt{t} -1}{t-1}} , \lim_{t \rightarrow 1}{ t^2} , \lim_{t \rightarrow 1}{\frac{t-1}{t} } \right) = \left( \lim_{t \rightarrow 1}{\frac{\sqrt{t} -1}{t-1}} , 1 , 0 \right).$$
Usando a Regra de L’Hospital, podemos facilmente ver que $$\lim_{t \rightarrow 1}{\frac{\sqrt{t} -1}{t-1}} = \lim_{t \rightarrow 1}{\frac{1}{2 \sqrt{t}}} = \frac{1}{2}$$ algo que pode, também, ser visto no gráfico da função f(t) = \dfrac{1}{2 \sqrt{t}} dado abaixo:
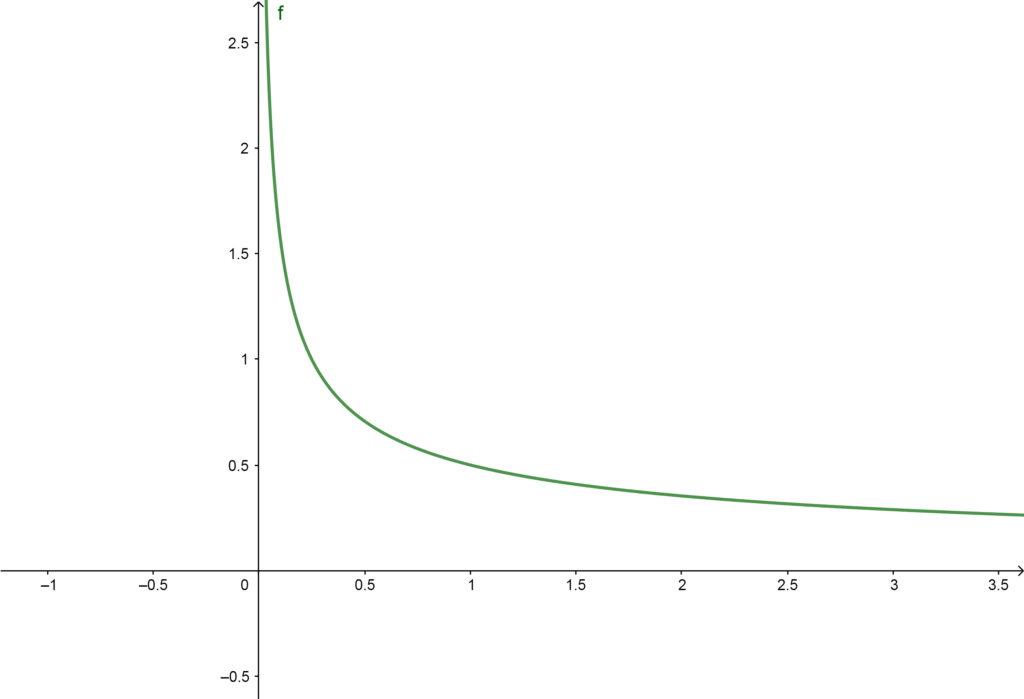
Portanto, $$ \lim_{t \rightarrow 1}{\vec{F}(t)} = \lim_{t \rightarrow 1}{\left( \frac{\sqrt{t} -1}{t-1} , t^2 , \frac{t-1}{t} \right)} = \left( \frac{1}{2} , 1 , 0 \right).$$
b) \lim_{t \rightarrow 0}{\vec{F}(t)} , onde \vec{F}(t) = \left( \dfrac{tg(3t)}{t} , \dfrac{e^{2t} - 1}{t}, t^3 \right)
SOLUÇÃO: Observe que teremos duas indeterminações nas duas primeiras funções componentes: $$i) \lim_{t \rightarrow 0}{\frac{tg(3t)}{t}}; \qquad ii) \lim_{t \rightarrow 0}{\frac{e^{2t} – 1}{t}}.$$
No primeiro caso, basta observar que $$\lim_{t \rightarrow 0}{\frac{tg(3t)}{t}} = \lim_{t \rightarrow 0}{\frac{sen(3t)}{t cos(3t)}} = 3 \lim_{t \rightarrow 0}{\frac{sen(3t)}{3t} \frac{1}{cos(3t)}}, $$ e usar o Primeiro Limite Fundamental: $$\lim_{t \rightarrow 0}{\frac{tg(3t)}{t}} = 3 \lim_{t \rightarrow 0}{\frac{sen(3t)}{3t} \frac{1}{cos(3t)}} = 3 \times 1 \times 1 = 3 .$$
No segundo caso, lembremos de um dos corolários do Segundo Limite Fundamental: \lim_{t \rightarrow 0}{\dfrac{a^t -1}{t} } = \ln{(a)} . Desta forma, temos um cálculo imediato: $$ \lim_{t \rightarrow 0}{\frac{e^{2t} – 1}{t}} = \lim_{t \rightarrow 0}{2 \frac{e^{2t} – 1}{2t}} = 2 \lim_{s \rightarrow 0}{\frac{e^{s} – 1}{s}} = 2 \ln{(e)} = 2.$$
Portanto, $$ \lim_{t \rightarrow 0}{\vec{F}(t)} = \lim_{t \rightarrow 0}{\left( \frac{tg(3t)}{t} , \frac{e^{2t} – 1}{t}, t^3 \right)} = $$ $$ = \left( \lim_{t \rightarrow 0}{\frac{tg(3t)}{t}} , \lim_{t \rightarrow 0}{\frac{e^{2t} – 1}{t}}, \lim_{t \rightarrow 0}{t^3} \right) = (3,2,0)$$
c) \lim_{t \rightarrow 2}{\vec{r}(t)} , onde \vec{r}(t) = \dfrac{t^3 - 8}{t^2 - 4} \vec{i} + \dfrac{\cos{(\pi /t)}}{t-2} \vec{j} +2t \vec{k}
SOLUÇÃO: Neste caso, novamente temos duas indeterminações nas primeiras funções componentes, e ambas serão atacadas usando a Regra de L’Hospital. Desta forma: $$\lim_{t \rightarrow 2}{\vec{r}(t)} = \left( \lim_{t \rightarrow 2}{ \frac{t^3 – 8}{t^2 – 4} } \right) \vec{i} + \left( \lim_{t \rightarrow 2}{\frac{\cos{(\pi /t)}}{t-2}} \right) \vec{j} + \left( \lim_{t \rightarrow 2}{2t} \right) \vec{k} = $$ $$ = \left( \lim_{t \rightarrow 2}{ \frac{3t^2}{2t} } \right) \vec{i} + \left( \lim_{t \rightarrow 2}{sen(\pi /t) \frac{\pi}{t^2}} \right) \vec{j} + 4 \vec{k} = $$ $$ = \left( \lim_{t \rightarrow 2}{ \frac{3t}{2} } \right) \vec{i} + \left( \lim_{t \rightarrow 2}{sen(\pi /t) \frac{\pi}{t^2}} \right) \vec{j} + 4 \vec{k} = 3 \vec{i} + \frac{\pi}{4} \vec{j} + 4 \vec{k} = \left( 3 , \frac{\pi}{4}, 4 \right) $$
2) Determine o conjunto de pontos de continuidade de cada uma das curvas abaixo. Justifique sua resposta.
a) \vec{F}(t) = t \vec{i} + \sqrt{t} \vec{j} + 3 \vec{k}
SOLUÇÃO: Observe que neste caso, as funções componentes x(t) = t e z(t) = 3 são funções escalares contínuas em todo o conjunto dos números reais Desta forma, será o intervalo de continuidade de y(t) = \sqrt{t} que determinará o intervalo de continuidade de \vec{F}(t) . Como sabemos, y(t) = \sqrt{t} é contínua para todo t \geq 0 . Portanto, \vec{F}(t) será uma função contínua para todo t \geq 0 .
b) \vec{F}(t) = \sqrt{t-1} \vec{i} + \sqrt{t+1} \vec{j} + e^t \vec{k}
SOLUÇÃO: Note que:
- x(t) = \sqrt{t-1} é uma função contínua para todo t \in \mathbb{R} tal que $$t-1 \geq 0 \Leftrightarrow t \geq 1 .$$
- y(t) = \sqrt{t+1} é uma função contínua para todo t \in \mathbb{R} tal que $$t+1 \geq 0 \Leftrightarrow t \geq -1 .$$
- z(t) = e^t é uma função contínua para todo t \in \mathbb{R} .
Desta forma, \vec{F}(t) será contínua na interseção dos intervalos de continuidade de suas funções componentes:
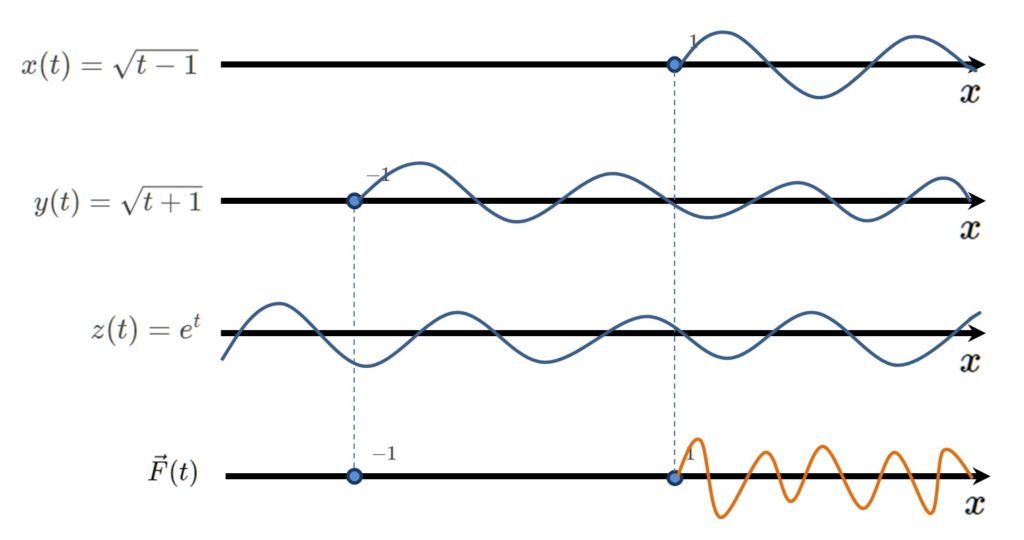
Portanto, o intervalo de continuidade de \vec{F}(t) serão todos os t \in \mathbb{R} tais que t \geq 1 .
3) Calcule \dfrac{d \vec{F}}{dt} e \dfrac{d^2 \vec{F}}{dt^2} .
a) \vec{F}(t) = \left( 3 t^2, e^{-t}, \ln{(t^2 +1)} \right)
SOLUÇÃO: $$\frac{d \vec{F}}{dt} = \left( 6t, – e^{-t} , \frac{2\,t}{{t}^{2}+1} \right)$$ $$ \frac{d^2 \vec{F}}{dt^2} = \left( 6 , e^{-t} , -\frac{2\,{t}^{2}-2}{{t}^{4}+2\,{t}^{2}+1} \right)$$
b) \vec{F}(t) = \left( t^{2/3}, \cos{t^2}, 3t \right)
SOLUÇÃO: $$\frac{d \vec{F}}{dt} = \left( \frac{2}{3\,{t}^{\frac{1}{3}}} , -2\,t\,\mathrm{sen}\left( {t}^{2}\right) , 3 \right)$$ $$ \frac{d^2 \vec{F}}{dt^2} = \left( -\frac{2}{9\,{t}^{\frac{4}{3}}} , -2\,\mathrm{sen}\left( {t}^{2}\right) -4\,{t}^{2}\,\mathrm{cos}\left( {t}^{2}\right) ,0 \right)$$
c) \vec{F}(t) = \left( sen(5t), cos(4t), -e^{-2t} \right)
SOLUÇÃO: $$\frac{d \vec{F}}{dt} = \left( 5 cos(5t), -4 sen(4t), 2 e^{-2t} \right)$$ $$ \frac{d^2 \vec{F}}{dt^2} = \left( -25 sen(5t), -16 cos(4t), -4 e^{-2t} \right)$$
4) Determine a equação da reta tangente à trajetória da função dada, no ponto dado, e esboce graficamente a curva e a reta.
a) \vec{F}(t) = \left( t^2, t \right) e \vec{F}(1) ;
SOLUÇÃO: Sabemos, deste artigo, que a equação da reta tangente à trajetória da função \vec{F}(t) , no ponto \vec{F}(t_0) é dada por $$ r: X = \vec{F}(t_0) + t \vec{F’}(t_0) .$$
Facilmente calculamos \vec{F}(1) = (1,1) e, como \vec{F'}(t) = \left( 2t, 1 \right) , então, \vec{F'}(1) = \left( 2, 1 \right). Portanto, a equação da reta tangente à trajetória da função \vec{F}(t) , no ponto \vec{F}(1) é $$r: (x,y) = (1,1) + t (2,1); \qquad t \in \mathbb{R}.$$
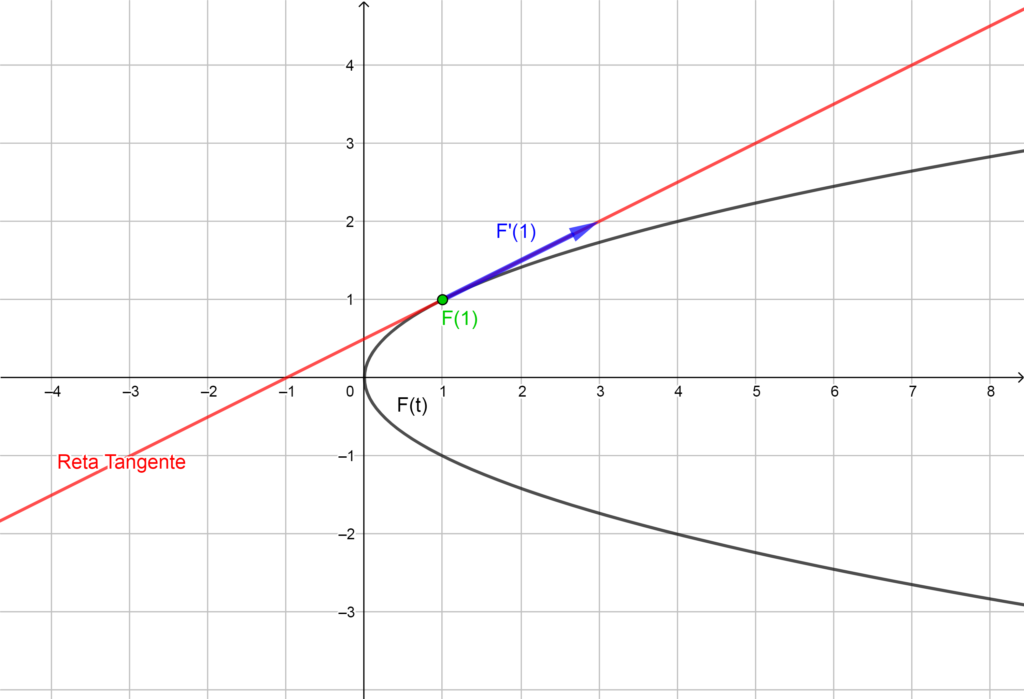
b) \vec{F}(t) = \left( \dfrac{1}{t}, \dfrac{1}{t}, t^2 \right) e \vec{F}(1) ;
SOLUÇÃO: Sabemos, deste artigo, que a equação da reta tangente à trajetória da função \vec{F}(t) , no ponto \vec{F}(t_0) é dada por $$ r: X = \vec{F}(t_0) + t \vec{F’}(t_0) .$$
Facilmente calculamos \vec{F}(1) = (1,1,1) e, como \vec{F'}(t) = \left( -\dfrac{1}{t^2}, - \dfrac{1}{t^2}, 2t\right) , então, \vec{F'}(1) = \left( -1, -1, 2 \right). Portanto, a equação da reta tangente à trajetória da função \vec{F}(t) , no ponto \vec{F}(1) é $$r: (x,y,z) = (1,1,1) + t (-1,-1,2); \qquad t \in \mathbb{R}.$$
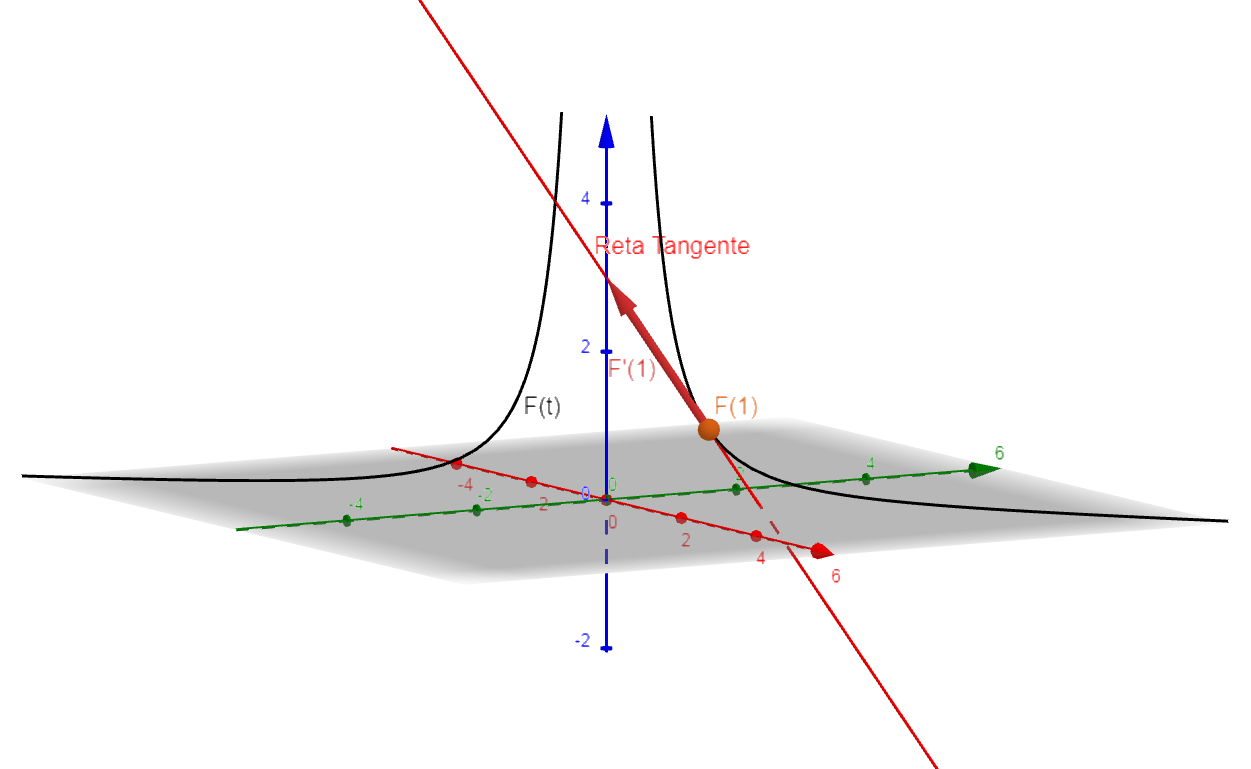
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
5) Sejam \vec{F}(t) = t \vec{i} + \vec{j} + e^t \vec{k} e \vec{G}(t) = \vec{i} + \vec{j} + \vec{k}. Calcule:
a) \int_{0}^{1}{\vec{F}(t) \wedge \vec{G}(t) dt} ;
SOLUÇÃO: Primeiramente, calculemos \vec{F}(t) \wedge \vec{G}(t) :
\begin{equation}
\vec{F}(t) \wedge \vec{G}(t) = \left|
\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
t & 1 & e^t\\
1 & 1 & 1
\end{array} \right| = (1 – e^t) \vec{i} + (e^t -t)\vec{j} +(t-1) \vec{k} .
\end{equation}
Desta forma, $$ \int_{0}^{1}{\vec{F}(t) \wedge \vec{G}(t) dt} = \int_{0}^{1}{\left[(1 – e^t) \vec{i} + (e^t -t)\vec{j} +(t-1) \vec{k} \right] dt} = $$ $$ =\vec{i}\int_{0}^{1}{(1 – e^t)dt} + \vec{j} \int_{0}^{1}{(e^t -t)dt}+\vec{k} \int_{0}^{1}{(t-1)dt} = $$ $$ = \left[ \vec{i}\,\left( t-{e}^{t}\right) -\vec{j}\,\left( \frac{{t}^{2}}{2}-{e}^{t}\right) +\vec{k}\,\left( \frac{{t}^{2}}{2}-t\right) \right]_{0}^{1} = $$ $$= – \frac{1}{2} \left( (2e-4) \vec{i}+ (3-2e)\vec{j}+ \vec{k} \right) = \left( -e+2 , -\frac{(3-2e)}{2} , -\frac{1}{2} \right)$$
b) \int_{0}^{1}{\vec{F}(t) \cdot \vec{G}(t) dt} ;
SOLUÇÃO: Primeiramente, calculemos \vec{F}(t) \cdot \vec{G}(t) : $$\vec{F}(t) \cdot \vec{G}(t) = ( t , 1, e^t ) \cdot (1,1,1) = t +e^t +1.$$ Portanto, $$ \int_{0}^{1}{\vec{F}(t) \cdot \vec{G}(t) dt} = \int_{0}^{1}{(t +e^t +1) dt} = $$ $$=\left[ \frac{{t}^{2}}{2}+t+{e}^{t}\right]_{0}^{1}=\frac{2\,e+1}{2}.$$
6) Seja \vec{F}(t) uma força, dependendo do tempo t , que atua sobre uma partícula entre os instantes t_1 e t_2 . Supondo \vec{F}(t) integrável em [ t_1 t_2 ] , o vetor $$ \vec{I} = \int_{t_1}^{t_2}{\vec{F}(t)dt} $$ é denominado impulso de \vec{F}(t) no intervalo [ t_1 t_2 ] . Calcule o impulso de cada uma das \vec{F}(t) no respectivo intervalo de tempo dado:
a) \vec{F}(t) = t \vec{i} + \vec{j} + t^2 \vec{k} com t_1 = 1 e t_2 = 2;
SOLUÇÃO: $$ \vec{I} = \int_{t_1}^{t_2}{\vec{F}(t)dt} = \int_{1}^{2}{\left( t \vec{i} + \vec{j} + t^2 \vec{k} \right) dt} = \left( \frac{3}{2} , 1 , \frac{7}{3} \right)$$
b) \vec{F}(t) = \dfrac{1}{t+1} \vec{i} + t^2 \vec{j} + \vec{k} com t_1 = 0 e t_2 = 1;
SOLUÇÃO: $$ \vec{I} = \int_{t_1}^{t_2}{\vec{F}(t)dt} = \int_{0}^{1}{\left(\frac{1}{t+1} \vec{i} + t^2 \vec{j} + \vec{k} \right) dt} = \left( \ln{(2)}, \frac{1}{3} , 1 \right)$$
Leia Mais:
- Curvas no Espaço | 2ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 1ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 3ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 5ª Lista de Exercícios Resolvidos



Pingback: Curvas no Espaço | 5ª Lista de Exercícios Resolvidos
Pingback: Curvas no Espaço | 6ª Lista de Exercícios Resolvidos