PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
As curvas e as superfícies de nível são formas de se visualizar funções de várias variáveis usando representações em dimensões inferiores. Este é um método semelhante ao da representação de uma paisagem tridimensional por meio de um mapa topográfico bidimensional.
Seja k um número real. Uma curva de nível, C_k de uma função z=f(x,y) é o conjunto de todos os pontos (x,y) \in D_f, tais que f(x,y)=k. Simbolicamente, $$C_k = \left\{(x,y) \in D_f ; f(x,y) = k \right\}.$$
Seja w=f(x,y,z), com (x,y,z) \in A \subset \mathbb{R} ^n, uma função real de três variáveis reais. O conjunto $$G_f=\left\{ (x,y,z,w) \in \mathbb{R} ^4 / w=f(x,y,z),\;\;\; (x,y,z) \in A \right\}$$ denomina-se gráfico de f. Seja k um número real. Uma curva de nível, C_k de uma função w=f(x,y,z) é o conjunto de todos os pontos (x,y,z) \in D_f, tais que f(x,y,z)=w. Simbolicamente, $$C_k = \left\{(x,y,z) \in D_f ; f(x,y,z) = k \right\}.$$
Abaixo vamos apresentar uma lista de exercícios sobre curvas e superfícies de nível funções com domínio no \mathbb{R} ^n simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.
Lista de Exercícios Resolvidos Sobre Curvas e Superfícies de Nível
1) Considere a função dada por z= \dfrac{y}{x-1} .
a) Determine o domínio e a imagem;
SOLUÇÃO: O domínio desta função é dado por $$ \{ (x,y) \in \mathbb{R} ^2 ; x-1 \neq 0 \}$$ $$ \{ (x,y) \in \mathbb{R} ^2 ; x \neq 1 \}$$ e a imagem é dada por \mathbb{R} , pois z= \dfrac{y}{x-1} assume valores positivos (quando o sinal do numerador e do denominador são iguais), negativos (quando o sinal do numerador e do denominador são diferentes) e zero (quando y=0)
b) Desenhe as curvas de nível.
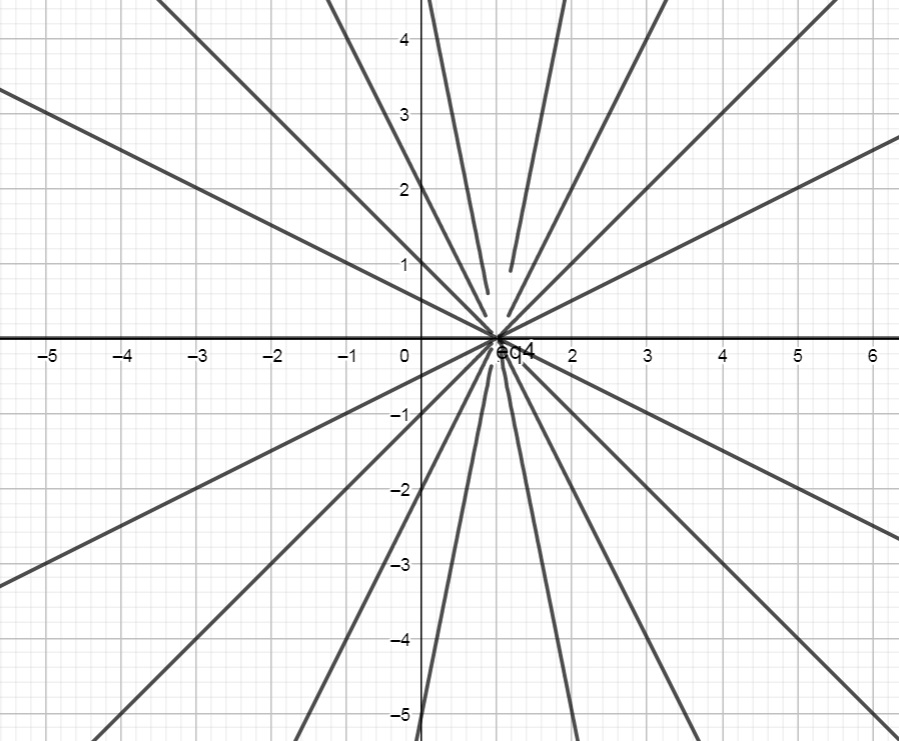
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
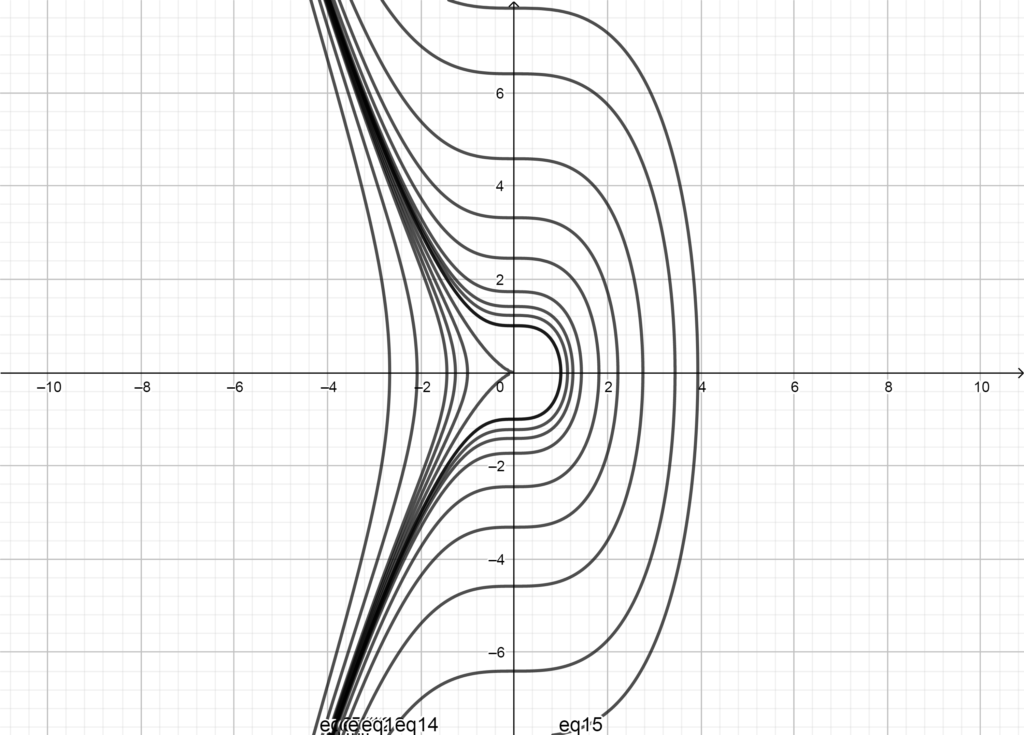
2) Esboce as curvas de nível de f(x,y) = x^3 + y^2 -1.
SOLUÇÃO: As curvas de nível desta função são dadas por k = x^3 + y^2 -1. Para valores de k específicos encontramos o gráfico abaixo
