Uma ferramenta matemática muito útil é o arredondamento de dados. Muitas vezes no deparamos com números com muitas casa decimais que tornariam os cálculos muito trabalhosos e apresentação de resultados nada elegantes, principalmente na estatística e na matemática financeira.
Para efetuar arredondamentos devemos observar o algarismo imediatamente posterior ao algarismo da casa decimal onde se deseja “arredondar”‘.
COMO FAZER ARREDONDAMENTO DE NÚMEROS?
Tome como exemplo o número 76,8954 e suponha que queremos arrendondá-lo para duas casas decimais. Assim, devemos analisar o algarismo imediatamente após o 9 (que se encontra na segunda casa decimal).
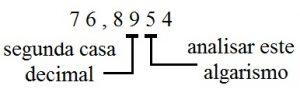 Como funciona o arredondamento numérico?
Como funciona o arredondamento numérico?
A análise deste algarismo será feita com base no valor assumido por ele no conjunto {0,1,2,3,4,5,6,7,8,9}
- Se o algarismo em questão for menor que 5, ou seja, 0,1,2,3 ou 4, desprezamos todos os algarismos posteriores a casa decimal desejada e conservamos o algarismo que está nesta casa decimal.
- Se o algarismo em questão for maior que 5, ou seja, 6,7,8 ou 9, desprezamos os algarismos após a casa decimal desejada e somamos um nesta casa decimal.
EXEMPLO
Vamos efetuar o “arredondamento” de alguns números:
1) 58,33958 com duas casas decimais:
Na terceira casa decimal temos o algarismo 9 (maior do que 5), logo desconsideramos os algarismos após a segunda casa decimal e somamos 1 na segunda casa decimal: 3+1=4.
Ou seja, o arredondamento de 58,33958 com duas casas decimais é 58,34.
2) 78,846970 com uma casa decimal;
Na terceira casa decimal temos o algarismo 4 (menor do que 5), logo desconsideramos os algarismos após a segunda casa decimal e preservamos o algarismo da segunda casa decimal.
Portanto, a aproximação de 58,33958 com uma casa decimal é 58,34.
Para melhor entender os dois exemplos temos o esquema mostrado na figura abaixo:

E se o algarismo da casa decimal for igual a 5?
Se o algarismo da casa decimal em questão for igual a 5 então observamos o algarismo imediatamente anterior.
Se este for par então desconsideramos todos os algarismos após a casa decimal desejada e conservamos a casa decimal em questão.
Se o algarismo anterior a casa decimal desejada for ímpar, então somamos um na casa decimal desejada e desconsideramos todos os algarismos seguintes.
EXEMPLO
Vamos efetuar o “arredondamento” de alguns números:
1) 72,465 com duas casa decimais;
- 5 é o algarismo da terceira casa decimal;
- algarismo imediatamente anterior (segunda casa decimal) é 6 que é par, logo preservamos o algarismo da segunda casa decimal.
Logo, o arredondamento de 72,465 com duas casas decimais é igual a 72,46.
2) 183,575 com duas casas decimais;
- 5 é o algarismo da terceira casa decimal;
- o algarismo imediatamente anterior (segunda casa decimal) é 7 que é ímpar, logo somamos um ao algarismo da segunda casa decimal.
Logo, o arredondamento de 183,575 com duas casas decimais é 183,58.
Em alguns casos existe a necessidade de realizar “arredondamentos” de números inteiros, que neste caso é efetuado para o inteiro mais próximo.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
OBSERVAÇÃO:
Suponha que queremos realizar o arredondamento do número 116 500 000 para a unidade de milhão mais próxima.
Temos um problema, 116 500 000 dista o mesmo de 116 000 000 e 117 000 000.
Neste caso, o critério utilizado é o mesmo aplicado a números decimais. Na unidade de milhão está o algarismo 6 e o algarismo imediatamente posterior é 5.
Como o algarismo da casa onde se efetuará o arredondamento é par então preservamos o 6 e
todos os algarismos seguintes serão substituídos por zeros.
Assim, 116 500 000 é a aproximado para a unidade de milhão mais próxima por 116 000 000
EXEMPLO
- 917 500 000 arredondado para a casa de dezena de milhão mais próxima é 920 000 000, pois está mais próximo de 917 500 000 que 910 000 000.
- 314 546 arredondado para a casa de milhar mais próxima é 315 000, pois está mais próximo de 314 546 que 314 000.
É importante observar que todos arredondamento gera erros e estes erros podem se acumular ao longo dos cálculos.
Sendo assim, é sempre importante ficar atento para que que este acumulo de erros não prejudique a análise dos dados.


Pingback: O que são Conjuntos Numéricos? Dos Naturais aos Complexos. - Matemática Simplificada