Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.

Expansões em meio-intervalo são expansões em Séries de Fourier que auxiliam em diversas soluções de problemas práticos que envolvem equações diferenciais parciais, como modelagens de ondas e dissipação do calor.

Dada uma função f(x) definida num intervalo (0,L), podemos expandir essa função como uma série de senos ou uma série de cossenos, gerando uma expansão par ou ímpar de f(x), colocando-a, ainda, como uma função de período 2L.

Uma série de Fourier de senos ou de cossenos (também denominada semi-série) é uma série que contém somente termos em senos ou em cossenos, respectivamente. Dada uma função f(x) definida num intervalo [0, L]], podemos usar a expansão em meio intervalo da Série de Fourier para obtermos uma função 2L-periódica, par ou ímpar equivalente a f(x).

Quando se deseja uma semi-série correspondente a determinada função esta é geralmente no intervalo (0,L) (que é metade do intervalo (-L, L); a fun é então especificada como sendo par ou ímpar, de modo que fique  claramente definido seu comportamento na outra metade do intervalo, à saber (-L, 0).

Mas antes, vamos estabelecer o conceito de funções pares e ímpares.

O Que São Funções Pares e Ímpares?

Uma função g(x) é dita par de g(-x)=g(x), para todo x.

Por outro lado, se g(-x)=-g(x), para todo x, então g é dita ímpar.

Por exemplo, a função f(x) = \cos{(n\pi x)}é par e g(x) = \sin{(n\pi x)} é ímpar.

Uma propriedade interessante das funções pares e ímpares é que se g(x) é uma função par, então $$\int \limits _{-\pi}^{\pi}{g(x) dx} = 2\int \limits _{0}^{\pi}{g(x) dx},$$ mas se g(x) é uma função ímpar, então $$\int \limits _{- \pi }^{\pi}{g(x) dx} = 0.$$

Outra propriedade importante é que o produto h = g.f de uma função ímpar g por uma função par f resulta em uma função ímpar.

De fato, $$h(-x) = g(-x).f(-x) = -g(x).f(x) = -h(x).$$

Série de Fourier de Senos e Cossenos.

A série de Fourier de um função periódica par f(x) que possui período igual a 2l é uma série de Fourier de cossenos dada por $$f(x) = \frac{1}{2} a_0 + \sum\limits _{n=1}^{\infty}{a_n \cos{\left( \frac{n \pi}{l} x \right)}}$$ com coeficientes $$a_0 = \frac{2}{l}\int _{0}^{l}{f(x)dx}, a_n = \frac{2}{l}\int _{0}^{l}{f(x)\cos{\left( \frac{n \pi}{l} x \right)}dx}.$$

Se f(x) é periódica ímpar com período igual a 2l então a série de Fourier de f é uma série de Fourier de senos dada por $$f(x) = \sum\limits _{n=1}^{\infty}{b_n \sin{\left( \frac{n \pi}{l} x \right)}}$$ com coeficientes $$b_n = \frac{2}{l}\int _{0}^{l}{f(x)\sin{\left( \frac{n \pi}{l} x \right)}dx}.$$

Expansão em Meio-Intervalo

Expansões em meio-intervalo são Séries de Fourier.

A ideia é simples e muito aplicável. Dada uma função f(x) definida num intervalo (0,L), podemos expandir essa função como uma série de senos ou uma série de cossenos, gerando uma expansão par ou ímpar de f(x), colocando-a, ainda, como uma função de período 2L.

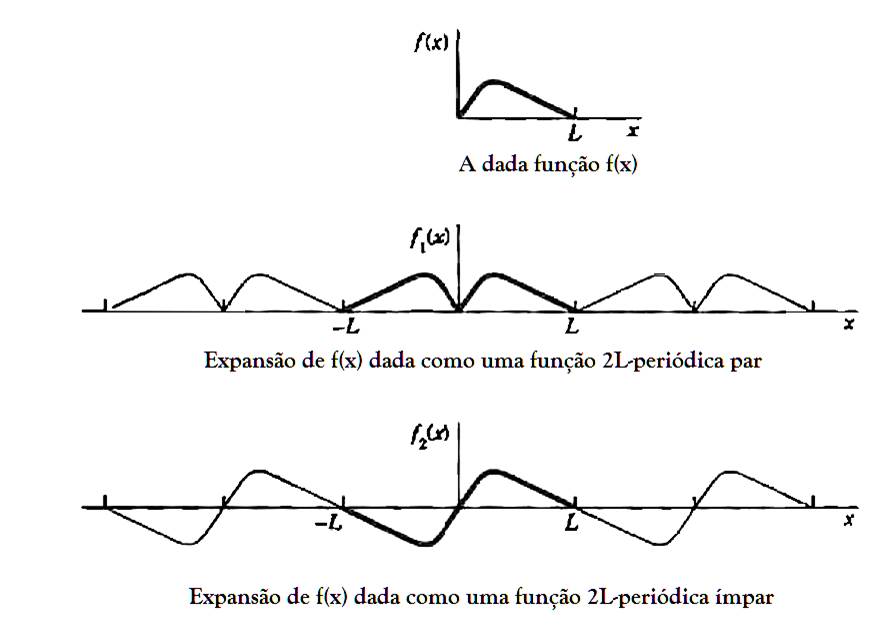
Essas séries são conhecidas como expansão de Fourier de meio intervalo da função f(x).

Vamos ilustrar essa ideia com um exemplo.

EXEMPLO:

Encontre a expansão de Fourier de meio intervalo da função
$$f(x)=\left\{\begin{array}{rl}
\frac{2kx}{l}; & 0<x<l/2\\
\\
\frac{2k(l-x)}{l}; &l/2 < x < l \end{array}\right. $$

O gráfico desta função é dado por

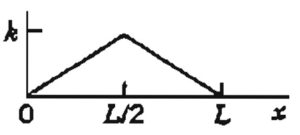
Primeiramente, temos que $$a_0 = \frac{1}{l}\left[\int _{0}^{l/2}{\frac{2kx}{l}dx} + \int ^{l}_{l/2}{\frac{2k(l-x)}{l}dx}\right] = \frac{k}{2}$$ e

$$ a_n = \frac{2}{l}\left[ \int _{0}^{l/2}{\frac{2kx}{l}\cos{\left( \frac{n \pi}{l} x \right)}dx} + \int ^{l}_{l/2}{\frac{2k(l-x)}{l} \cos{\left( \frac{n \pi}{l} x \right)}dx}\right]$$
$$ =\frac{4k}{l^2}\left[ \int _{0}^{l/2}{x \cos{\left( \frac{n \pi}{l} x \right)}dx} + \int ^{l}_{l/2}{(l-x) \cos{\left( \frac{n \pi}{l} x \right)}dx} \right]$$

$$ = \frac{4k}{l^2}\left( \left[ \frac{l^2}{2n\pi}\sin\left( \frac{n \pi}{2} \right) + \frac{l^2}{n^2 \pi ^2}\left( \cos{\left(\frac{n \pi}{2} \right)} -1 \right) \right] + \right.  $$ $$ + \left. \left[ -\frac{l^2}{2n\pi}\sin\left( \frac{n \pi}{2} \right) – \frac{l^2}{n^2 \pi ^2}\left(\cos{\left(n \pi \right)} – \cos{\left(\frac{n \pi}{2} \right)}\right) \right]\right) = $$

$$= \frac{4k}{n^2 \pi ^2} \left( 2\cos{\left(\frac{n \pi}{2} \right)} -\cos{\left(n \pi \right)} – 1 \right) $$

$$ = \frac{-16k}{(4n -2)^2 \pi ^2} $$

Desta forma, a primeira expansão de Fourier de meio intervalo da função f(x) é

$$f(x) = \frac{k}{2}+ \sum _{n=1}^{\infty}{\frac{4k}{n^2 \pi ^2} \left( 2\cos{\left(\frac{n \pi}{2} \right)} -\cos{\left(n \pi \right)} – 1 \right) \cos{\left( \frac{n \pi}{l} x \right)}} , $$ ou seja, $$ f(x) = \frac{k}{2}+\sum _{n=1}^{\infty}{\frac{-16k}{(4n -2)^2 \pi ^2}} \cos{\left( \frac{n \pi}{l} x \right)}$$ que é um expansão periódica par em série de cossenos de Fourier ilustrada na figura abaixo:

Analogamente, podemos encontrar uma expansão ímpar, de senos para f(x) com $$b_n = \frac{8k}{n^2 \pi ^2} sen \left( \frac{n \pi}{2} \right) = (-1)^{n+1} \frac{8k}{n^2 \pi ^2} .$$

Portanto, a expansão em meio intervalo neste caso é dado por $$f(x) = \sum _{n=1}^{\infty}{(-1)^{n+1} \frac{8k}{n^2 \pi ^2} \sin{\left( \frac{n \pi}{l} x \right)}},$$ sendo ilustrada na figura abaixo:

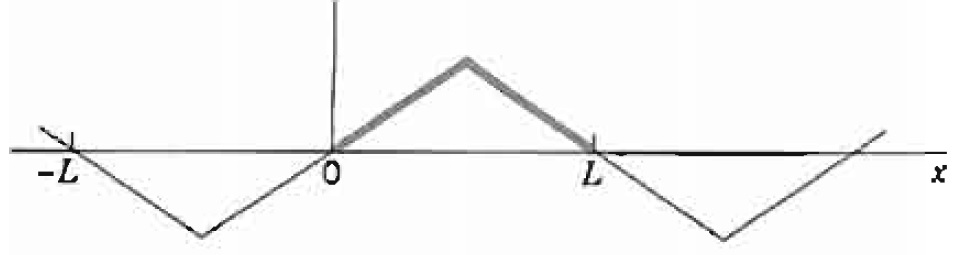
Lista de Exercícios Resolvidos Sobre a Expansão em Meio-Intervalo:

Abaixo estão todas as nossas listas de exercícios resolvidos sobre a Expansão em Meio-Intervalo. Basta clicar no link em azul e ser redirecionado para a página dos exercícios:

• 1ª Lista de Exercícios Resolvidos – Expansão em Meio Intervalo |

Leia Mais:

• O Que São Funções Periódicas? Definição e Exemplos.
• Séries de Fourier | Os Coeficientes de Fourier
• Séries de Fourier | História, Definição e Condições de Existência.
• Desafios de Matemática | 11 problemas para desafiar sua mente
• Efeito Borboleta | Edward Lorenz e a Teoria do Caos
  

Assista Nossa Video-Aula Sobre Expansão em Meio-Intervalo