Transformada de Laplace Inversa | Frações Parciais, Convolução e Translação

Entender a Transformada de Laplace Inversa é um processo importante para aplicar apropriadamente a Transformada de Laplce nas suas diversas aplicações, principalmente na solução de EDO’s lineares e PVI’s correspondentes que pode ser resumido em três passos: 1) a EDO dada é transformada em uma equação algébrica; 2) esta equação é solucionada por manipulações algébricas; e 3) a solução obtida no item 2 é transformada de volta obtendo a solução do problema original dado.

Quando aplicamos a Transformada de Laplace a uma função f(t) , obtemos uma outra função F(s) e denotamos isso simbolicamente por \mathscr{L} \left[f(t) \right] = F(s).

Agora, iremos trabalhar com o problema inverso, ou seja, dada uma função  F(s)tentaremos encontrar uma função f(t) cuja transformada de Laplace seja F(s).

Dizemos então que f(t) é a Transformada de Laplace Inversa de F(s) e escrevemos $$f(t) = \mathscr{L} ^{-1} \left[F(s)\right].$$

OBSERVAÇÃO: A Transformada de Laplace Inversa de uma função F(s) pode não ser única. Porém, podemos garantir que se duas funções f(t) e g(t) são contínuas por partes em [0, \infty) e de ordem exponencial, então, se a Transformada de Laplace de ambas for igual, pode-se mostrar que f(t) e g(t) são essencialmente iguais, diferindo apenas em seus pontos de descontinuidade.

A Fórmula de Mellin Para a Transformada de Laplace Inversa

Uma formula da integral da transformada inversa de Laplace, chamada de integral de Bromwich, a integral de Fourier-Mellin , e fórmula da inversa de Mellin, é dada pela integral de linha:

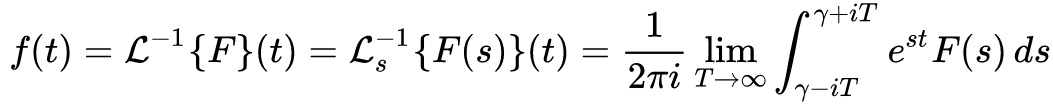
onde  a integração é feito ao longo da linha vertical Re(s) = \gamma no plano complexo em que \gamma é maior do que a parte real de todas as singularidades de F(s). Isto garante que o caminho de contorno esta na região de convergência. Se todas as singularidades estão à esquerda do meio do plano, ou F(s) é uma função suave em – ∞ < Re(s) < ∞, então \gamma pode ser definido para zero e acima da formula da integral inversa tornando-se idêntica à Transformada Inversa de Fourier.

Tabela de Transformada de Laplace Inversa

À partir da Tabela de Transformada de Laplace podemos deduzir uma tabela similar para a Transformada de Laplace Inversa.

Além disso, conseguimos estabelecer alguns casos gerais de inversão partindo das transformadas básicas como vemos na tabela abaixo:

A Linearidade da Transformada de Laplace Inversa

A Transformada de Laplace Inversa é, assim como a Transformada de Laplace, definida por uma integral que usa variáveis complexas.

Desta forma, essa natureza da definição da Transformada de Laplace Inversa como uma integral garante o fato dela ser linear, ou seja, para quaisquer duas funções F(s) e G(s) cujas transformadas existem e quaisquer constantes a e b a transformada de aF(s) + bG(s) existe e \mathscr{L}^{-1}[aF(s) + bG(s)]= a \mathscr{L}^{-1}[F(s)] + b \mathscr{L}^{-1}[G(s)].

EXEMPLO

Encontre a Transformada Inversa de Y (s) = \dfrac{1}{s^5}

Para usarmos a tabela acima e a linearidade da transformada de Laplace Inversa verificamos que n = 4 e então multiplicamos e dividimos por 4!. Segue que $$ \mathscr{L}^{-1} \left[  \frac{1}{s^5} \right] = \frac{1}{4!} \mathscr{L}^{-1} \left[  \frac{4!}{s^5} \right] = \frac{1}{24} t^4.$$

EXEMPLO

Encontre a Transformada Inversa de Y (s) = \dfrac{1}{s^2 + 64}

Observando que \omega ^2 = 64 , multiplicamos e dividimos por 8 e usamos a linearidade, encontramos: $$ \mathscr{L}^{-1} \left[  \frac{1}{s^2 + 64} \right] = \frac{1}{8} \mathscr{L}^{-1} \left[  \frac{8}{s^2 + 64} \right] = \frac{1}{8} sen(8t).$$

EXEMPLO

Calcule \mathscr{L} ^{-1} \left( \dfrac{3s+5}{s^2 +7} \right):

Essa fração pode ser escrita como a soma de duas frações:

$$ \frac{3s+5}{s^2 +7} = \frac{3s}{s^2 +7}  + \frac{5}{s^2 +7} .$$

Pela linearidade da transformada inversa e pela tabela, encontramos:

$$ \mathscr{L} ^{-1} \left( \frac{3s+5}{s^2 +7} \right) = \mathscr{L} ^{-1} \left( \frac{3s}{s^2 +7}  \right) + \mathscr{L} ^{-1} \left( \frac{5}{s^2 +7} \right) = $$ $$ = 3 \mathscr{L} ^{-1} \left( \frac{s}{s^2 +(\sqrt{7})^2}  \right) + \frac{5}{\sqrt{7}} \mathscr{L} ^{-1} \left( \frac{\sqrt{7}}{s^2 +(\sqrt{7})^2} \right) =$$ $$ = 3 cos (\sqrt{7} t) + \frac{5}{\sqrt{7}} sen(\sqrt{7} t).$$

Frações Parciais

O uso de Frações Parciais é muito importante para encontrar a Transformada de Laplace Inversa. Em suma, qualquer função racional (quociente de polinômios) expressa-se como soma de frações parciais.

Consideremos a função racional
$$ f(t) = \frac{P(t)}{Q(t)} $$
onde P e Q são polinômios. É possível expressar f como soma de frações mais simples desde que o grau de P seja menor que o
grau de Q. Se o grau de P for maior ou igual ao grau de Q,
então primeiro dividimos os polinômios,
$$ \frac{P(t)}{Q(t)} = S(t) + \frac{R(t)}{Q(t)}, $$ onde S(t) e R(t) são também polinômios.

Denominadores Redutíveis do 2º Grau

Sejam \alpha, \beta, m, n\in\R, com \alpha\neq \beta. Então existem A,B\in \R tais que

1. \frac{mx+n}{(x-\alpha)(x-\beta)} = \frac{A}{x-\alpha} + \frac{B}{x-\beta};
2. \frac{mx+n}{(x-\alpha)^2} = \frac{A}{x-\alpha} + \frac{B}{(x-\alpha)^2}.

Denominadores Redutíveis do 3º Grau

Sejam \alpha, \beta, \gamma, m, n, p\in\R, com \alpha,\beta,\gamma \neq 0. Então existem A,B,C\in\mathbb{R} tais que

1)\frac{mx^2+nx+p}{(x-\alpha)(x-\beta)(x-\gamma)} = \frac{A}{x-\alpha} + \frac{B}{x-\beta} + \frac{C}{x-\gamma};
2) \frac{mx^2+nx+p}{(x-\alpha)(x-\beta)^2} = \frac{A}{x-\alpha} + \frac{B}{x-\beta} + \frac{C}{(x-\beta)^2};
3)\frac{mx^2+nx+p}{(x-\alpha)^3} = \frac{A}{x-\alpha} + \frac{B}{(x-\alpha)^2} +\frac{C}{(x-\alpha)^3}.

Denominadores Irredutíveis do 2º Grau

1) Se \frac{P(x)}{ax^2+bx+c}, onde P é um polinômio e \Delta = b^2-4ac < 0, então devemos reescrever o denominador como soma de quadrados, ou seja, fazemos um completamento de quadrados.

2) Sejam m, n, p, a, b, c, \alpha\in\R tais que \Delta = b^2-4ac<0. Então existem A,B,D \in \R tais que $$ \frac{mx^2+nx+p}{(x-\alpha)(ax^2+bx+c)} =
\frac{A}{x-\alpha} + \frac{Bx+D}{ax^2+bx+c}\ . $$

Leia Mais: Exemplos de como usar Frações Parciais

O Teorema da Convolução

Se duas funções f e g satisfazem as condições de existência da Transformada de Laplace, e f e g sejam, respectivamente, suas transformadas, então o produto H=FG é a transformada da convolução de f e g.

Ou seja, $$\mathscr{L}(f).\mathscr{L}(g) = \mathscr{L}(f*g),$$ por consequência, $$\mathscr{L}^{-1}(F.G) = f*g .$$

Quando Não Existe a Transforma Inversa?

Nem toda função de s é transformada de Laplace de alguma função contínua por partes de ordem exponencial.

TEOREMA

Seja f(t) contínua por partes em [0, \infty ) e de ordem exponencial para t > T , então $$ \lim_{s \rightarrow \infty} \mathscr{L}^{-1} \left( F(s) \right) = 0 .$$

EXEMPLO:

As funções F_1 (s) = s^2 e F_2 (s) = \dfrac{s}{s+1} não são transformadas de Laplace de nenhuma função por partes de ordem exponencial, pois nenhuma delas tende a zero quando s \rightarrow \infty . Dizemos que \mathscr{L}^{-1} \left( F_1 (s) \right) e \mathscr{L}^{-1} \left( F_2 (s) \right) não existem.

Calculando a Transformada de Laplace Inversa

Vamos usar a fórmula da inversão dada no teorema acima e as fórmulas deduzidas no último exemplo para encontrar a inversa das transformadas abaixo:

1. Y(s)=\frac{s-1}{s^2-s-2}

Observe que $$Y(s)=\frac{s-1}{s^2-s-2}\Rightarrow Y=\frac{s-1}{(s+1)(s-2)}$$

Por frações parciais, obtemos

$$Y(s)=\frac{s-1}{(s+1)(s-2)} = \frac{1/3}{(s-2)}+ \frac{2/3}{(s+1)}$$

Logo, $$y(t) = \mathscr{L}^{-1} \left( \frac{1/3}{(s-2)}+ \frac{2/3}{(s+1)} \right) $$ que pela linearidade da transformada, y(t) é dado por $$y(t) = \frac{1}{3} e^{2t} + \frac{2}{3}e^{-t} $$

2. F(s) =\mathscr{L} (f) = \frac{3s-137}{s^2+2s+401}.

Primeiramente, olhamos para o denominador:

s^2 + 2s +401 = (s+1)^2 + 400 = (s+1)^2 + 20^2

Com essa estrutra de denominador, encaixamos nossa transformada nos itens 11 e 12 da nossa tabela de Transformadas de Laplace, com a=-1 e ω = 20.

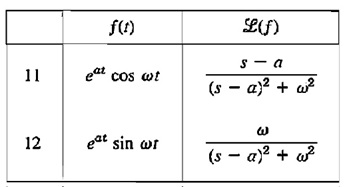
Agora, olhamos para o numerador:

3s-137 = 3s+3 - 140 = 3(s+1) - 140.

Daí,

f(t) =  \mathscr{L}^{-1} \left( \frac{3s-137}{s^2+2s+401} \right)

f(t) =  \mathscr{L}^{-1} \left( \frac{3(s+1) - 140}{(s+1)^2 + 20^2}  \right)

f(t) =  \mathscr{L}^{-1} \left( \frac{3(s+1)}{(s+1)^2 + 20^2} \right) - \mathscr{L}^{-1} \left( \frac{140}{(s+1)^2 + 20^2} \right)  

f(t) =  3 \mathscr{L}^{-1} \left( \frac{(s+1)}{(s+1)^2 + 20^2} \right) - 7 \mathscr{L}^{-1} \left( \frac{20}{(s+1)^2 + 20^2}  \right) 

f(t) =  3 e^{-t}\cos{(20t)} - 7 e^{-t}\sin{(20t)}  

3) Y(s) = \left( \frac{2s^3+s^2+8s+6}{(s^2 + 4)(s^2 +1)}\right)

Por frações parciais

$$\frac{2s^3+s^2+8s+6}{(s^2 + 4)(s^2 +1)} = \frac{as+b}{(s^2 + 4)} + \frac{cs+d}{(s^2 +1)}$$
ou seja,
$$2s^3+s^2+8s+6 = (as+b)(s^2 + 1) + (cs+d)(s^2 +4).$$

Assim,

$$a+c = 2$$ $$b+d = 2$$ $$a+4c = 8 $$ e $$b+4d=6$$

Por consequência, a=0, c=2, b=-2/3 e d=5/3.

$$\frac{2s^3+s^2+8s+6}{(s^2 + 4)(s^2 +1)} = \frac{-2/3}{(s^2 + 4)} + \frac{2s+5/3}{(s^2 +1)}$$

Daí, $$y(t) = -1/3 \mathscr{L}^{-1} \left( \frac{2}{(s^2 + 4)}\right) + 2 \mathscr{L}^{-1} \left(\frac{s}{(s^2 + 1)} \right) + 5/3 \mathscr{L}^{-1} \left( \frac{1}{(s^2 + 1)} \right) $$, ou seja

$$y(t) = -1/3 \sin{2t} + 2 \cos{t} + 5/3 \sin{t}$$

4) Y = e^{-s} \left( \frac{1}{(s+1)}\right) - e^{-s} \left(\frac{1}{(s+2)} \right)

Pela Transformada inversa

\begin{eqnarray*}
y & = & \mathscr{L}^{-1} \left( e^{-s} \left( \frac{1}{(s+1)}\right) – e^{-s} \left(\frac{1}{(s+2)} \right) \right)\\
\\
& = & \mathscr{L}^{-1} \left( e^{-s} \left( \frac{1}{(s+1)}\right)\right) – \mathscr{L}^{-1} \left( e^{-s} \left(\frac{1}{(s+2)}\right) \right)\\
\\
& = & u(t-1) \left(\mathscr{L}^{-1} \left( \frac{1}{(s+1)}\right) – \mathscr{L}^{-1} \left(\frac{1}{(s+2)}\right) \right)\\
\\
& = & u(t-1) \left(e^{(t-1)}-e^{2(t-1)} \right)\\
\\
& = & \left\{ \begin{array}{ll}
0; & t<1\\
e^{(t-1)}-e^{2(t-1)}; & t \geq 1
\end{array} \right.
\end{eqnarray*}

5.F(s) = \left( \dfrac{2}{s^2(s^2+4)} \right) (usando a convolução).

$$\mathscr{L} ^{-1} \left( \frac{2}{s^2(s^2+4)} \right) = \mathscr{L} ^{-1} \left( \frac{1}{s^2} \times \frac{2}{s^2+4} \right) = t * sen(2t).$$

Como t * sen(2t) = \int_{0}^{t}{(t- \tau) sen (2 \tau) d\tau} = \dfrac{2t - sen(2t)}{4} , então $$\mathscr{L} ^{-1} \left( \frac{2}{s^2(s^2+4)} \right) = \frac{2t – sen(2t)}{4}.$$

Lista de Exercícios Resolvidos Sobre Transformada de Laplace Inversa:

• Transformada de Laplace Inversa | Lista de Exercícios Resolvidos

Leia Mais:

• Transformada de Laplace | Das Definições Básicas à Função Delta
• A Convolução e a Transformada de Laplace
• Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos
• Integração por Frações Parciais | Técnicas de Primitivação

Assista nossa vídeo-aula sobre a Transformada de Laplace Inversa: