A representação geométrica dos números complexos é feita no plano cartesiano, onde o eixo x é denominado eixo real e o eixo y é o eixo imaginário. Neste artigo estabelecemos de forma menos rigorosa os aspectos topológicos do plano complexo necessários ao estudo das funções complexas.
Os números representados no eixo dos x são da forma (x,0) = x+0i , ou seja, são os números reais puros, por isto este é chamado de eixo real. Já os complexos representados no eixo dos y , e por isso chamado de eixo imaginário, são da forma 0 + yi = yi. Sendo assim, o número complexo z=x+yi é plotado como o par ordenado (x,y).
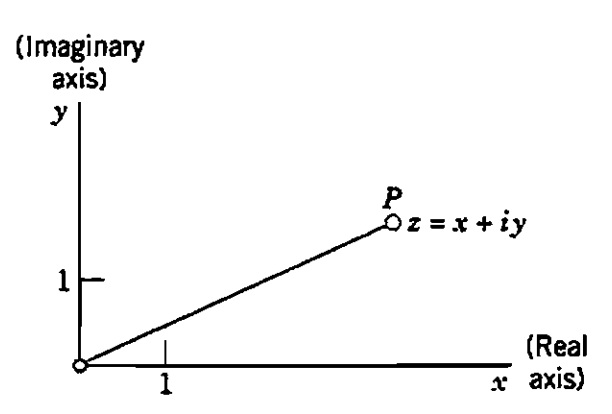 Diagrama de Argand: O Plano Complexo
Diagrama de Argand: O Plano Complexo
O plano xy onde são representados os números complexos é chamado de plano complexo ou diagrama de Argand. Jean-Robert Argand foi um matemático suíço amador mais conhecido como um dos primeiros a fornecer uma descrição geométrica dos números complexos. Argand publicou em 1806 uma interpretação geométrica dos números complexos, o Diagrama de Argand. Esta descrição geométrica dos números complexos também é associada ao nome de Gauss, embora anteriormente a Gauss, Caspar Wessel também tenha descrito o diagrama.
A adição e a subtração de dois números complexos, de acordo com a “regra do paralelogramo”, pode ser representado n plano complexo da seguinte forma:
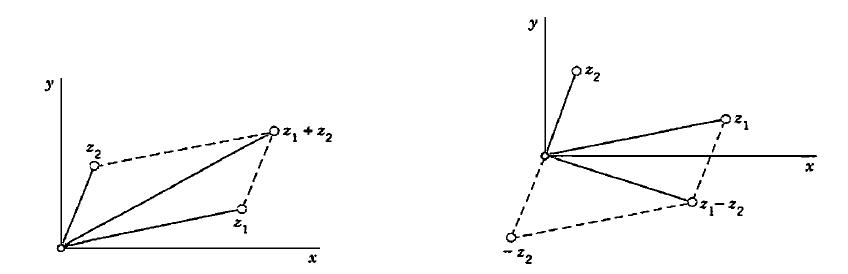 Soma de Números Complexos no Plano de Argand
Soma de Números Complexos no Plano de Argand
O complexo conjugado também pode ser representado no plano complexo. Para exemplificar considere z = 5 + 2i.
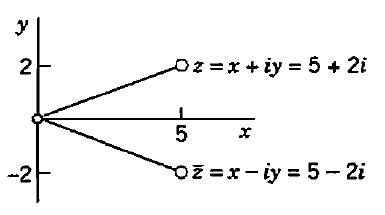 Representação do complexo conjugado no Plano de Argand
Representação do complexo conjugado no Plano de Argand
A Topologia do Plano Complexo
Agora devemos considerar algumas importantes regiões e curvas no plano complexo e suas representações através de equações e inequações. O termo. conjunto de pontos no plano complexo significa que tomaremos uma coleção finita ou infinita de números complexos. Agora, vamos estabelecer conceitos topológicos para estes conjuntos de pontos.
DISCOS NO PLANO COMPLEXO, FRONTEIRA E VIZINHANÇA
Lembrando que a distância entre dois números complexos, z e a no plano de Argand pode ser dado por \| z - a \| . Assim, segue que um círculo C de raio \rho com centro no ponto a pode ser dado pela equação $$ \| z -a \| = \rho . $$
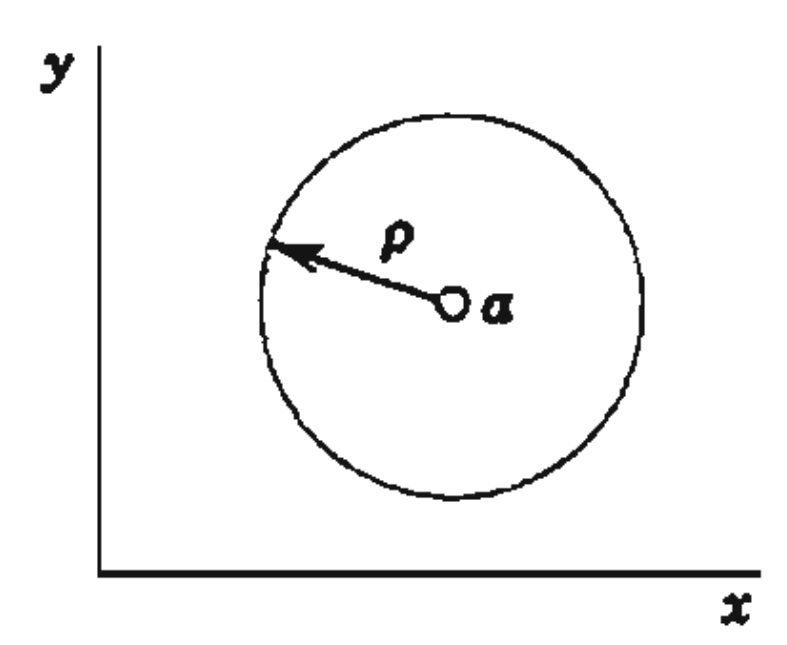 Círculo no Plano Complexo.
Círculo no Plano Complexo.
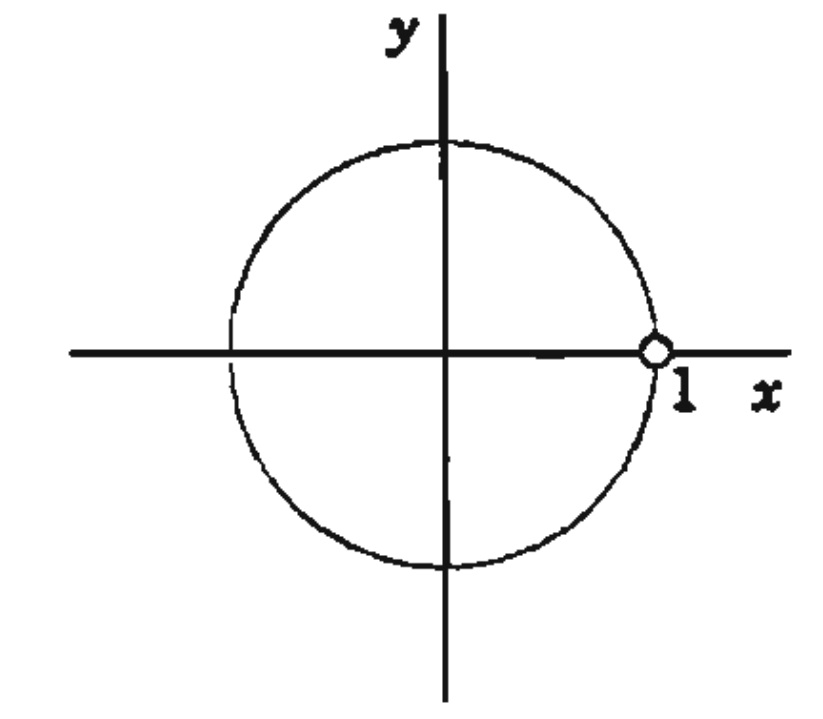
A equação $$ \| z \| = 1 $$ representa o importante círculo unitário, ou seja, o círculo de raio 1 com centro na origem. Este círculo tem um papel importante em várias considerações teóricas e práticas quando estudamos funções complexas.
 Círculo Unitário
Círculo Unitário
Consequentemente, a inequação $$ \| z -a \| < \rho $$ assegura que o ponto z está dentro do círculo C, ou seja esta inequação representa o interior desta circunferência. Tal região é chamada de disco circular, ou mais precisamente disco circular aberto, em contraste ao disco circular fechado $$ \| z -a \| \leq \rho $$ que consiste do interior da circunferência e sua fronteira.
Este disco circular aberto é também chamado de vizinhança do ponto a . Obviamente, a tem uma infinidade de vizinhanças, cada uma correspondendo a um certo valor de \rho > 0 .
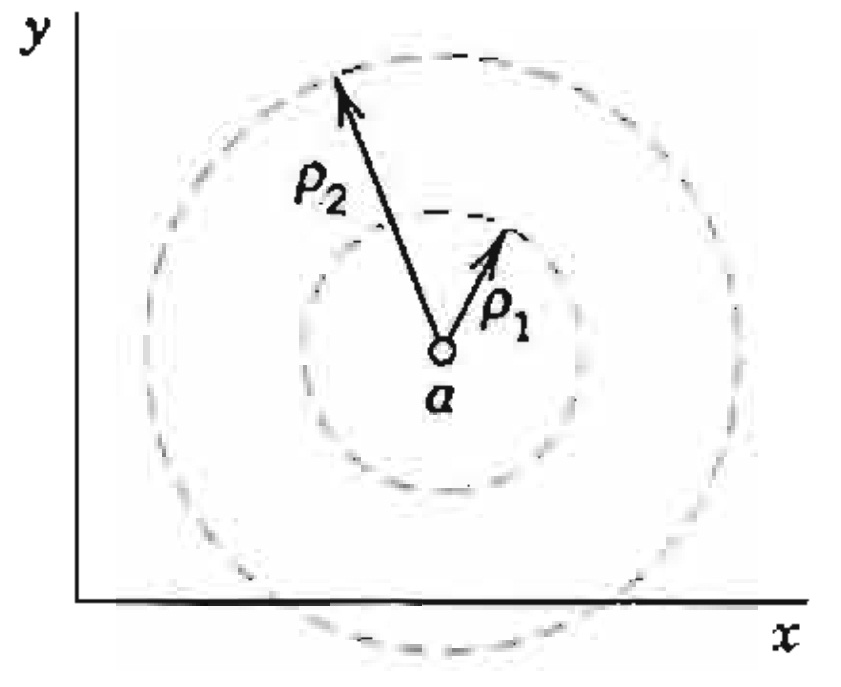
De forma análoga, a inequação $$ \| z -a \| > \rho $$ representa o exterior do círculo C. Desta forma, a região entre dois círculos concêntricos de raios 0 < \rho _1 < \rho _2 que pode ser representada na forma $$ \rho _1 < \| z -a \| < \rho _2 ,$$ onde a é o centro de ambos os círculos. Tal região é chamada de anel.
 Anel no Plano Complexo
Anel no Plano Complexo
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
CONJUNTOS ABERTOS E FECHADOS NO PLANO COMPLEXO
Desta forma, um conjunto S é chamado de aberto se cada um de seus pontos possui uma vizinhança contendo apenas pontos de S. São exemplos de conjuntos abertos no plano complexo os pontos interiores de um círculo ou de um quadrado, assim como como os pontos do semi-plano Re(z) = x > 0 .
Em contrapartida, uma bola fechada não é um conjunto aberto pois todas as vizinhanças de cada um de seus pontos de fronteira possui pontos que não pertencem à bola fechada. Os conjuntos que possuem esta característica no plano complexo são chamados de conjuntos fechados.
Um ponto de fronteira de um conjunto S é um ponto onde todas as vizinhanças possuem pontos que pertencem e pontos que não pertencem ao conjunto.
Um conjunto é chamado de limitado se todos os seus pontos podem ser colocados dentro de uma bola aberta de raio suficientemente grande. São exemplos de conjuntos limitados os pontos de um quadrado no plano, enquanto os pontos do semi-plano Re(z) = x > 0 formam um conjunto ilimitado.
O conjunto S será chamado de conexo se quaisquer dois pontos podem ser ligados por por uma curva inteiramente contida em S. Geralmente um conjunto aberto e conexo é chamado de domínio. Uma região é um conjunto consistindo de um domínio e todos os seus pontos de fronteira.
Leia Mais:
- Números Complexos | Primeiras Definições e Operações Elementares
- Números Complexos | A Forma Polar e as Operações Elementares
- Uma Introdução às Funções de Variáveis Complexas
- Funções de Variáveis Complexas | Limite e Continuidade


