Pré-Cálculo: Teoria dos Conjuntos | Lista de Exercícios Resolvidos

Um conjunto é uma palavra para designar uma coleção de objetos, e eles são sempre indicados por letras maiúsculas. Já os objetos de um conjunto são denominados elementos e são indicados por letras minúsculas. Dizemos que a pertence à um conjunto A se a é um elemento de A e indicamos esta relação por $$a \in A.$$ Caso contrário, se a não pertence ao conjunto A, então utilizamos a seguinte notação para esta relação $$a \notin A.$$

O conjunto A será um subconjunto de B se A \subset B. Também podemos dizer que A é parte de B, que A está incluído em B, ou contido em B. Os conjuntos numéricos, por exemplo, obedecem à cadeia de inclusão: $$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}.$$

A união de A com B é dada por $$C=A\cup B = \left\{x; x\in A\;\;\;ou\;\;\;x\in B\right\}$$ enquanto a interseção é dada por $$A\cap B = \left\{x; x\in A\;\;\;e\;\;\;x\in B\right\}.$$ A diferença entre os conjuntos A e   B é o conjunto $$ A – B = \{ x; x \in A \;\;\; e \;\;\; x \notin B\},$$ ou seja, o conjunto formado pelos elementos de A que não estão em   B .

Introdução à Teoria dos Conjuntos | Lista de Exercícios Resolvidos

1) Sendo A = {1, 2}, B = {2, 3} e C = {3, 4}, determine (A \cup B \cup C) - (C \cap B) :

SOLUÇÃO:  Observe que (A \cup B \cup C) = \{ 1,2,3,4 \} e (C \cap B) = \{3 \} . Logo, (A \cup B \cup C) - (C \cap B) = \{1,2,4\}.

2) Se A ,  B e A \cap B têm, respectivamente, 27, 17 e 10 elementos, determine o número de elementos de 

a) A \cup B

b) A - B  

SOLUÇÃO: Usando um diagram de Venn podemos perceber que

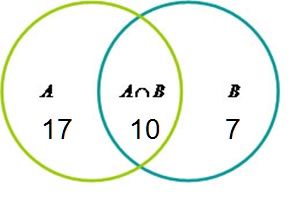
Logo, A \cup B tem exatamente, 17 + 17 = 34 elementos, enquanto B - A , que são os elementos de B que não estão em A possui exatamente 7 elementos.

3) No desenho abaixo, a região hachurada é dada por qual das opções abaixo:

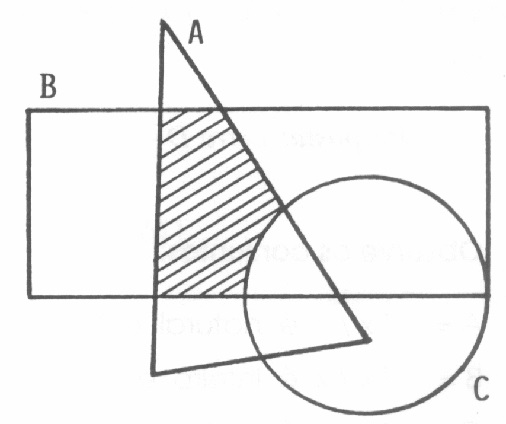
1. (A \cup B) – C
2. (A \cap B) – C
3. (A \cap C) – B
4. (A \cup C) – B

SOLUÇÃO: Letra B, pois são todos os elementos que aparecem tanto em A quanto B exceto os elementos de C.

4) Sendo A = \{2n; n \in \mathbb{N} \;\;\; e \;\;\; 3 < n \leq 11 \} e B = \{2n+1; n \in \mathbb{N} \;\;\; e \;\;\; 3 < n \leq 12 \} , então quais são os conjuntos A \cup B e A \cap B .

SOLUÇÃO: Observe que o conjunto A é o conjunto de todos os números pares entre 3 e 11, que é dado por $$ A = \{ 4,6,8,10\} $$, enquanto B é o conjunto de todos os números ímpares entre 3 e 12, que é dado por $$ B = \{3,5,7,9,11\}.$$ Logo, $$ A \cup B = \{4, 5, 6, 7, 8, 9, 10, 11\} ; \qquad e \qquad  A \cap B = \emptyset $$

5) Demonstre as propriedades da união de conjuntos abaixo:

a) A \cup \emptyset = A

SOLUÇÃO:

 x \in A \cup \emptyset \Leftrightarrow x \in A\;\;\; ou \;\;\; x \in \emptyset. Como o conjunto vazio não contêm nenhum elemento então x \in A \cup \emptyset \Leftrightarrow x \in A..

b) A \cup A = A

SOLUÇÃO:

x \in A \cup A \Leftrightarrow x \in A\;\;\; e \;\;\; x \in A. \Leftrightarrow x \in A.

c) A \cup B = B \cup A

SOLUÇÃO:

x \in A \cup B \Leftrightarrow x \in A\;\;\; ou \;\;\; x \in B \Leftrightarrow x \in B\;\;\; ou \;\;\; x \in A \Leftrightarrow x \in B \cup A.

d) (A \cup B) \cup C = A\cup (B \cup C)

SOLUÇÃO:

\begin{eqnarray*}
x \in (A \cup B) \cup C & \Leftrightarrow & x \in (A \cup B)\;\;\; ou\;\;\; x \in C \\
&\Leftrightarrow& x \in A \;\;\;ou\;\;\; x \in B\;\;\; ou\;\;\; x \in C \\
&\Leftrightarrow& x \in A\;\;\; ou\;\;\; x \in (B \cup C) \\
&\Leftrightarrow& x \in A\cup (B \cup C)
\end{eqnarray*}

e) A \cup B = A \Leftrightarrow B \subset A

SOLUÇÃO:

(\Rightarrow) x \in B \Rightarrow x \in A \cup B \Rightarrow x \in A \Rightarrow B \subset A

(\Leftarrow) x \in A \cup B \Leftrightarrow x \in A\;\;\;ou\;\;\; x \in B \subset A \Leftrightarrow x \in A

Leia Mais:

• Introdução à Teoria dos Conjuntos | Pré Cálculo
• O que são Conjuntos Numéricos? Dos Naturais aos Complexos.
• Números Reais | Introdução à Topologia da Reta Real
• Números Reais | Definição, Operações Elementares, Intervalos e Módulo