O legado de Edward Lorenz e seu Efeito Borboleta permanecem como um testemunho da capacidade humana de encontrar significado no aparente caos do universo.
Explore a fascinante jornada de Edward Lorenz e a descoberta do ‘Efeito Borboleta‘, revelando ordem oculta em meio ao caos. Este artigo mergulha na história por trás da famosa frase de Lorenz, examina o enigma das equações não-lineares e destaca as aplicações e importância dessa descoberta revolucionária. Com citações do próprio Lorenz, descubra como pequenas perturbações podem ter um impacto surpreendente e saiba como essa ideia continua a moldar nossa compreensão de sistemas complexos.

Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Este artigo explora a descoberta de Edward Lorenz, um matemático do Massachusetts Institute of Technology, na década de 60, que revelou um comportamento estranho nas equações matemáticas usadas para previsões meteorológicas.
Na década de 60, um matemático do Massachusetts Institute of Technology (MIT), Edward Lorenz, fez uma descoberta que iria revolucionar nossa compreensão de sistemas complexos e caóticos.
Enquanto tentava melhorar as previsões meteorológicas, Lorenz tropeçou em um comportamento estranho e aparentemente caótico em suas equações matemáticas.
As equações não-lineares estudadas por Lorenz apresentaram propriedades intrigantes, resultando em ordens ocultas em meio ao aparente caos.
Com a ajuda dos computadores, Lorenz conseguiu visualizar e descrever essas descobertas, que são cruciais para entender fenômenos complexos, como o clima, os batimentos cardíacos e os processos neurais.

O Enigma das Equações Não-Lineares
Lorenz estava usando equações não-lineares em sua pesquisa, um tipo de matemática que lida com relações complexas entre variáveis.
Normalmente, equações científicas produzem resultados previsíveis quando aplicadas a problemas semelhantes.
No entanto, as equações que Lorenz estava usando para modelar o clima mostraram algo completamente inesperado.
Pequenas variações nos valores iniciais das variáveis resultavam em previsões drasticamente diferentes.
Isso era como se um carro saísse de São Paulo às 19 horas e outro às 19h15min, e a equação previa que o segundo carro chegaria à Lituânia, em vez do Rio de Janeiro.
O comportamento errático e imprevisível dessas equações intrigou Lorenz.
O Papel dos Computadores e o Efeito Borboleta
Embora o estudo de equações não-lineares já existisse há muito tempo, a revolução veio com o advento dos computadores.
Foi a capacidade de calcular e visualizar rapidamente as soluções dessas equações que permitiu a Lorenz entender a complexidade subjacente.
Os computadores revelaram uma ordem oculta em meio ao caos, semelhante a um eletrocardiograma com um defeito especial.
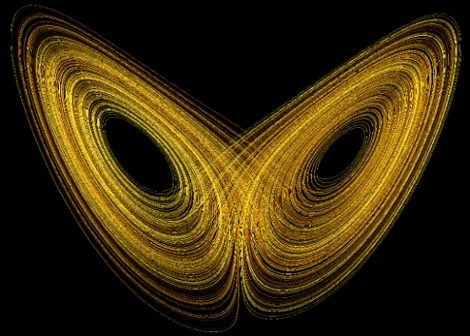
O fenômeno que Lorenz descobriu ficou conhecido como a “Borboleta de Lorenz”.
Em vez de ziguezagues erráticos nas medidas de temperatura e pressão, as equações não-lineares transformaram esses padrões em um movimento grácil e regular, semelhante a um oito deitado.
Essa figura representava a ordem oculta que Lorenz encontrou nas equações caóticas do clima.
A Citação Histórica de Edward Lorenz:
Edward Lorenz, ao descrever o impacto das pequenas perturbações nas condições iniciais, afirmou: “O bater das asas de uma borboleta no Brasil pode desencadear um tornado no Texas.”
Esta frase icônica encapsula a ideia central do Efeito Borboleta e da sensibilidade extrema às condições iniciais.
Aplicações e Importância
A descoberta de Lorenz teve implicações profundas em várias áreas da ciência.
Ela ajudou a entender fenômenos complexos, como o clima, onde pequenas mudanças nas condições iniciais podem resultar em previsões amplamente divergentes.
Além disso, essa compreensão também se aplicou a outros sistemas caóticos, como os batimentos cardíacos e os padrões de disparo dos neurônios.

A Teoria do Caos
Dizer que as asas de uma borboleta provocariam um tornado não se torna tão absurdo do ponto de vista matemático, se pudermos garantir variabilidade adequada de eventos e tempo suficientemente grande para o desenrolar de tais eventos.
Mesmo impossível na prática, pela simples impotência em executar previsões para longos períodos de tempo, esse argumento soa muito plausível, matematicamente falando.
Isaac Newton, um dos pais do Cálculo Diferencial, mudou a ciência no século XVIII ao traduzir fenômenos naturais em linguagem matemática, sendo pioneiro na exploração das possibilidades preditivas destes fenômenos, além de nos mostrar que poderíamos explorar o comportamento de todos os fenômenos se tivéssemos informações suficientes.
Sendo assim, às vezes só ainda não possuímos uma arcabouço satisfatório de informações para fugir de nossa impotência frente às previsões para longos períodos de tempo.
A semente da Teoria do Caos fora plantada por Henri Poincaré, um dos maiores matemáticos de todos os tempos, em seus estudos em dinâmica conservativa, principalmente em um artigo de 1889, que estudava o Problema Newtoniano de Três Corpos.
Poincaré foi seguido por Birkhoff, já na primeira metade do século XX, que sedimentou o terreno para a exploração da teoria por nomes como Lorenz, o astrofísico Michel Hénon e grandes matemáticos como Stephen Smale, David Ruelle e tantos outros.
Por definição pouco rigorosa, um sistema caótico seria aquele que sofre alterações drásticas em seu resultado quando são feitas mínimas alterações em suas condições iniciais.
Este comportamento caótico está diretamente ligado ao conceito de entropia, que seria, essencialmente, a taxa de dissipação da informação.
Esta taxa, por sua vez, pode ser descrita com precisão de diversas maneiras como, por exemplo, o tempo de duplicação (tempo necessário para uma incerteza se duplicar), sendo a questão cabal neste momento, quantos períodos de duplicação são necessários para que este evento altere o todo?
Essa questão é muito pertinente visto que a presença do caos possui um efeito devastador sobre as previsões advindas de modelos científicos, todavia, algumas vezes, o caos controlado pode até ser útil a algumas áreas.
Grosso modo, a Teoria do Caos estuda o comportamento de sistemas dinâmicos não-lineares (traduzindo: várias equações diferenciais complicadas que devem ser solucionadas simultaneamente) que são altamente sensíveis a perturbações em suas condições iniciais.
A natureza determinística (isto é, um modelo matemático que determina os resultados, exatamente, a partir das condições iniciais) do sistema faz dele pouco previsível, sendo este comportamento conhecido como caos determinístico, ou simplesmente caos.
O alicerce matemático desta teoria está alicerçada sobre terreno complexo que envolve teoria qualitativa robusta de equações diferenciais, imersão no mundo da geometria fractal, bem como uma boa capacidade de abstração.
Claro que todos estes elementos são mais do que interessantes (principalmente a este apaixonado pelas equações diferenciais que vos escreve), mas fogem aos escopo da postagem de apenas introduzir, superficialmente, belos conceitos da ciência.
Todavia, saiba que tudo no universo esta sob o domínio do Caos, ou é produto do Caos, sendo que James Marti, em 1991, especulou que “o Caos poderia muito bem ser a nova ordem mundial”.
Pode não ser bem assim, mas claramente temos uma nova forma de observar e interpretar dados.

Conclusão
A história da Borboleta de Lorenz destaca a importância de explorar o desconhecido e desafiar as suposições em nossa busca por entender o mundo complexo que nos rodeia.
As equações não-lineares de Lorenz revelaram a existência de ordem oculta no caos, demonstrando que até os sistemas mais imprevisíveis podem conter padrões subjacentes.
Essa descoberta continua a influenciar a ciência e a matemática modernas, mostrando que a beleza da ordem pode emergir mesmo nos lugares mais inesperados.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Portanto, o legado de Edward Lorenz e sua Borboleta permanecem como um testemunho da capacidade humana de encontrar significado no aparente caos do universo.
Como observou James Marti, o caos pode não ser a nova ordem mundial, mas certamente nos proporcionou uma nova maneira de observar e interpretar o universo e os dados que ele nos apresenta.
5 Livros para Entender a Ciência da Teoria do Caos:
Explore um mundo de conhecimento através desta lista cuidadosamente selecionada. Essas obras abrangem uma ampla gama de temas, desde a influência do acaso nas nossas vidas até as complexidades da ciência, incluindo sistemas complexos e teorias do caos.
Descubra os segredos do cosmos e da física fundamental, ampliando sua visão do universo. Além disso, mergulhe na interconexão entre matemática e vida em uma obra recentemente publicada que explora tópicos contemporâneos relacionados ao caos, complexidade e sistemas dinâmicos.
Esses livros oferecem uma oportunidade única de expandir seu horizonte de conhecimento e explorar os mistérios do mundo que nos cerca.
1) “O Andar do Bêbado: Como o Acaso Determina Nossas Vidas” por Leonard Mlodinow
Se você deseja explorar como o acaso molda nossas vidas e descobrir a ordem por trás do caos aparente, adquira este livro e embarque em uma jornada fascinante pela complexidade do destino humano.
2) “Complexity: A Guided Tour” por Melanie Mitchell
Para uma análise profunda dos sistemas complexos e como a ordem emerge do caos, esta edição atualizada de 2018 é essencial. Adquira-a agora e mergulhe na ciência da complexidade.
3) “A Realidade Oculta: Universos Paralelos e as Profundas Leis do Cosmo” por Brian Greene
Para uma exploração cativante sobre o universo, desde teorias do caos até a possibilidade de múltiplos universos, pegue este livro e amplie sua visão do cosmos.
4) “Será Que Deus Joga Dados?”, por Ian Stewart
Descubra as respostas fascinantes sobre o universo e a matemática no livro ‘Será Que Deus Joga Dados?’ de Ian Stewart. Desvende os mistérios da ciência agora!”
5) “Sync: The Emerging Science of Spontaneous Order”, por Steven Strogatz
Explore o fascinante mundo da ordem espontânea na ciência com “Sync: The Emerging Science of Spontaneous Order” por Steven Strogatz. Desvende os segredos da sincronia e da matemática por trás dela hoje mesmo!
Leia Mais:
- Equação do Jogador: Conheça a matemática da aposta esportiva
- Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
- Os 7 Melhores Livros de Ficção Para Quem Ama Matemática
- Da ficção à realidade: As 5 maravilhas da engenharia inspiradas por Júlio Verne
- Os 5 Melhores Livros Para Estudar Cálculo Diferencial e Integral


