O Teorema de Green No Plano | Enunciado e Exercícios Resolvidos.

O Teorema de Green no Plano garante que Integrais duplas sobre uma região plana podem ser transformadas em integrais de linha sobre uma região limitada a vice-versa. Esta transformação na prática possui mais interesse teórico.

Teorema de Green no Plano:  Seja R uma região fechada e limitada no plano xy cuja fronteira consiste de uma quantidade finita de curvas regulares. Sejam f(x,y) e g(x,y) funções contínuas e cujas derivadas parciais \dfrac{\partial f}{\partial y} e \dfrac{\partial g}{\partial x} também são contínuas em algum domínio R. Então: $$\int\limits_{R} \int \left( \frac{\partial g}{\partial x} – \frac{\partial f}{\partial y} \right) dx dy= \int\limits_{C}\left( fdx +gdy \right).$$

Vamos considerar agora L=L(x,y,z), M=M(x,y,z) e N=N(x,y,z) funções definidas e contínuas numa região R de espaço de modo que $$\vec{F}(x,y,z) = L(x,y,z)i+M(x,y,z)j+N(x,y,z)k$$ seja um campo vetorial definido no aberto R e seja C um arco regular, todo contido em R com representação paramétrica $$P(t) = x(t) i + y(t) j +z(t) k\;\;\;\;a\leq t \leq b$$ que descreve um movimento em R.

Vamos definir a integral de linha de \vec{F}, ao longo do arco C, como sendo $$\int\limits_{C}{Ldx+Mdy+Ndz} = \int\limits_{C}{\vec{F}(P(t)).dP} $$ onde F(P) = (L(P(t)),M(P(t)), N(P(t))) e dP = (x'(t)dt, y'(t)dt, z'(t)dt) = P'(t)dt.

Esta integral é denominada de integral de linha de segunda espécie e sua forma clássica é dada por $$\int\limits_{a}^{b}{[Lx’+My’+Nz’]dt}$$

Teorema de Green no Plano – 1ª Lista de Exercícios Resolvidos

1) Considere o campo vetorial \vec{F}(x,y) = (y+x^2\cos{x}, 2x-y^2\sin{y}). Calcule $$\oint\limits_{C}{F(P).dP}$$ onde C é a circunferência com centro em (0,0) e raio igual a 1:

SOLUÇÃO: Usando o Teorema de Green no Plano, obtemos:

\begin{eqnarray*}
\oint\limits_{C}{F(P).dP} & = & \int\limits_{R} \int \left( 2 – 1\right) dx dy\\
& = & \int\limits_{0}^{2\pi} \int\limits_{0}^{1}r dr d\theta\\
& = & \pi
\end{eqnarray*}

2) Use o Teorema de Green para calcular a área da região encerrada pela hipociclóide $$x^{2/3} + y^{2/3} = a^{2/3}.$$

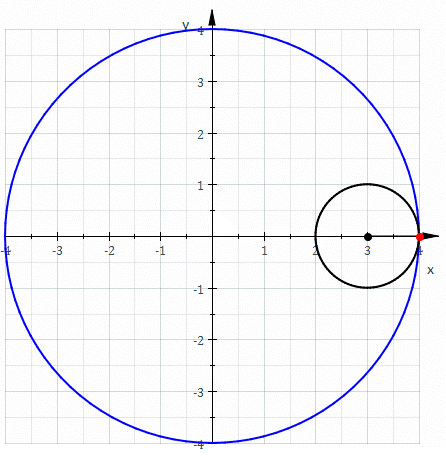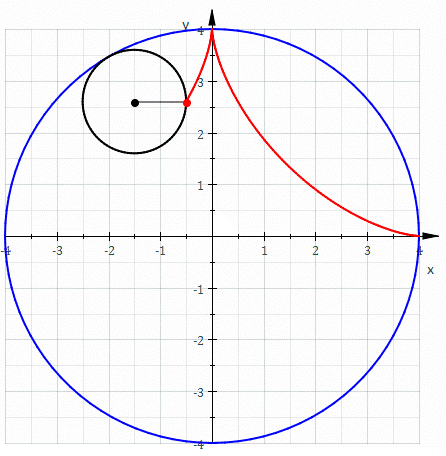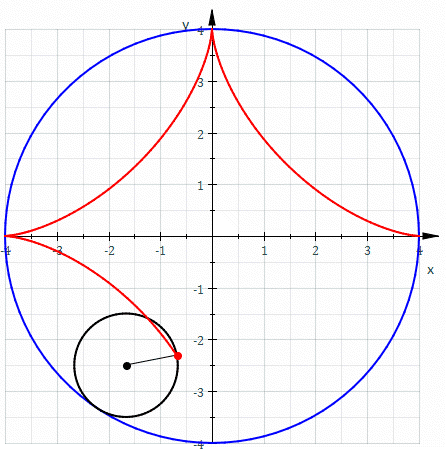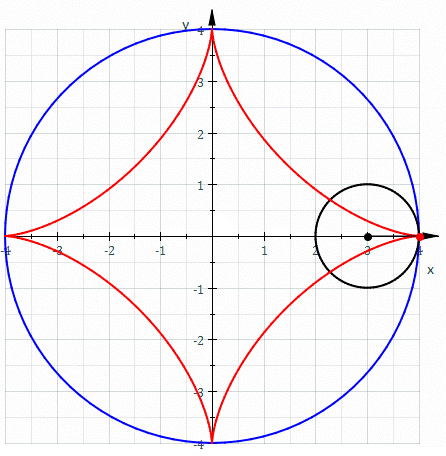SOLUÇÃO: Note-se que esta curva pode ser parametrizada como $$P(t) = a(cos^3 \theta , sen^2 \theta ), \qquad 0 \leq \theta \leq 2 \pi .$$

Teremos, então, para a área procurada A, $$ A = \frac{3 a^2}{2} \int\limits_{0}^{2 \pi}{\left( sen^2 \theta cos^2 \theta + cos^2 \theta sen^4 \theta  \right)d \theta} =$$ $$ \frac{3 a^2}{2} \int\limits_{0}^{2 \pi}{\left( sen^2 \theta cos^2 \theta \right)d \theta} = \frac{3 a^2}{8}\int\limits_{0}^{2 \pi}{sen^2 (2 \theta)  d \theta} = \frac{3 \pi a^2}{8} .$$

3) Calcule $$\oint\limits_{C} \left(3y- e^{sen(x)} \right)dx+ \left( 7x + \sqrt{y^4+1}\right)dy$$ onde C é o círculo com centro na origem e raio r = 3.

SOLUÇÃO: 

A região R limitada por C é o disco x^2 + y^2 \leq 9 , desta forma, mudando para coordenadas polares após aplicarmos o Teorema de Green no plano obtemos: $$ \oint\limits_{C} \left(3y- e^{sen(x)} \right)dx+ \left( 7x + \sqrt{y^4+1}\right)dy  = \\ = \iint\limits_{D}\left[ \frac{\partial}{\partial x} \left( 7x + \sqrt{y^4+1}\right) –  \frac{\partial}{\partial y} \left(3y- e^{sen(x)} \right) \right]dxdy = \\ = \int\limits_{0}^{2 \pi}\int\limits_{0}^{3}(7-3)r dr d \theta = \\ = 4\int\limits_{0}^{2 \pi} d \theta \int\limits_{0}^{3} rdr = 36 \pi .$$

Leia Mais:

• Integral de Linha de 1ª Espécie | 1ª Lista de Exercícios Resolvidos
• Integral de Linha de Campos Vetoriais | 1ª Lista de Exercícios Resolvidos
• Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano
• Integral de Superfície | Teoremas de Stokes e da Divergência

Assista nossa vídeo aula sobre o Teorema de Green