O Princípio de Dirichlet, também conhecido como o Princípio das Gavetas, de enunciado e compreensão bastante simples, nos permite chegar a conclusões impressionantes e nada óbvias.
Ele diz o seguinte:
Se n+1 objetos forem distribuídos em n gavetas, então pelo menos uma gaveta conterá pelo menos dois objetos.
Por exemplo, é possível, através desse princípio, provar que em Belo Horizonte há duas pessoas com o mesmo número de fios de cabelos, sem ter que convocar nenhum cidadão para realizar a contagem.
De fato, pois em Belo Horizonte tem mais de 1.000.000 de habitantes e nenhum morador daquela cidade tem mais que 500.000 cabelos.
Observe porém que este princípio não diz como achar duas pessoas de Belo Horizonte com o mesmo número de fios de cabelo. Se quiséssemos exibir tais pessoas teríamos que realizar a contagem.
Esse princípio também conhecido como O Princípio da Casa dos Pombos:
Se n+1 pombos forem distribuídos em n casas, então pelo menos uma delas conterá pelo menos 2 pombos.
Esse é um assunto bastante recorrente em provas de Raciocínio Lógico, sendo geralmente cobrado dentro do chamado “Raciocínio Matemático“.
Mas também esse é um princípio usado para resolver problemas práticos advindo de aplicações da Teoria dos Jogos
QUEM FOI DIRICHLET?
Peter Gustav Lejeune Dirichlet, (1805 – 1859) foi um matemático alemão que fez contribuições valiosas para a teoria dos números, análise e mecânica.
Ele lecionou nas universidades de Breslau (1827) e Berlim (1828-55), e em 1855 sucedeu Carl Friedrich Gauss na Universidade de Göttingen.
Dirichlet fez contribuições notáveis ainda associadas ao seu nome em muitos campos da matemática.
Em 1837, Dirichlet propôs o conceito moderno de uma função y = f (x) na qual, para cada x, está associado um único y.
Em mecânica, ele investigou o equilíbrio dos sistemas e a teoria do potencial, o que o levou ao problema de Dirichlet relativo às funções harmônicas com valores de fronteira prescritos.
APLICAÇÃO NA TEORIA DOS JOGOS
A Teoria dos Jogos é um ramo da Matemática Aplicada que estuda situações em que duas ou mais partes se confrontam, no sentido de maximizarem seus ganhos.
Em geral, a Teoria de Jogos pode ser usada quer para prever o resultado de uma situação de confronto, quer para aconselhar um dos confrontantes a tomar a melhor decisão.
O início da Teoria dos Jogos ganhou força pelas mãos dois matemáticos renomados: John von Neumann e John Nash.
O jogo SIM foi introduzido por Gustavus Simmons em 1969.
Abaixo, usaremos o Princípio das Gavetas de Dirichlet para provar que o jogo não pode acabar sem completar algum triângulo, ou seja, sempre existe um perdedor neste jogo.
O JOGO DO SIM
Dados os vértices de um hexágono regular, dois jogadores (laranja e azul) alternam unindo dois vértices com um segmento da sua cor.
Quem completar um triângulo monocromático perde.
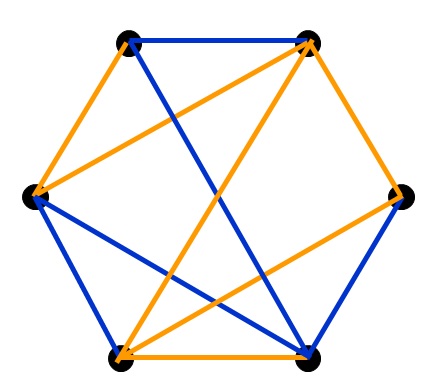 Nessa simulação de um jogo do SIM, o jogador representado pela cor laranja perdeu.
Nessa simulação de um jogo do SIM, o jogador representado pela cor laranja perdeu.
O jogo do SIM seria bastante desinteressante se o empate fosse possível. Mas acontece que não é.
Para ver isto, suponhamos que temos o resultado de um jogo completo ( pois do contrário alguém completou um triângulo monocromátrico e já perdeu ).
Escolhamos um vértice qualquer, digamos P.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Como de cada vértice partem cinco segmentos coloridos e só há duas cores, então pelos menos três destes segmentos tem a mesma cor, laranja, por exemplo.
Sejam A, B e C as extremidades desses três segmentos.
Se AB ou BC for laranja, então o laranja perde, e portanto não houve empate.
Suponhamos então que AB e BC sejam azuis.
Que cor então pode ter o segmento AC?
Qualquer escolha leva a um triângulo laranja ou a um triângulo azul, e portanto algum dos jogadores venceu, e consequentemente não houve empate.
Conclusão: no jogo do SIM sempre há um vencedor e um perdedor.
A base do raciocínio anterior, que garantiu a existência de três segmentos da mesma cor saindo de P, é uma generalização do Princípio de Dirichlet ou o Princípio das Gavetas.

