PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
A análise combinatória visa desenvolver métodos que permitam contar o número de elementos de um conjunto, sendo estes elementos, agrupamentos formados sob certas condições.
Em outras palavras, a Análise Combinatória é um conjunto de procedimentos que possibilita a construção, sob certas circunstâncias, de grupos diferentes formados por um número finito de elementos de um conjunto.
Por exemplo:
Suponha que uma pessoa quer viajar de Recife a Porto Alegre passando por São Paulo. Sabendo que há 5 roteiros diferentes para chegar à São Paulo partindo de Recife e 4 roteiros diferentes para chegar a Porto Alegre partindo de São Paulo, de quantas maneiras possíveis essa pessoa poderá viajar de Recife à Porto Alegre?
Esse é o tipo de problema resolvido com técnicas matemáticas de Análise Combinatória.
A Análise Combinatória nasce da necessidade de calcular o número de possibilidades existentes nos jogos gerou o estudo dos métodos de contagem.
Grandes matemáticos se ocuparam com o assunto: o italiano Niccollo Fontana (1500-1557), conhecido como Tartaglia, e os franceses Pierre de Fermat (1601-1665) e Blaise Pascal (1623-1662).
Dois conceitos são fundamentais para a análise combinatória: Fatorial de um número e o Princípio Fundamental da Contagem (árvore de possibilidades).
Os três tipos principais de agrupamentos são as Permutações, os Arranjos e as Combinações. Estes agrupamentos podem ser simples, com repetição ou circulares.
Na maior parte das vezes, tomaremos conjuntos Z com n elementos e os grupos formados com elementos de Z terão k elementos, isto é, k será a taxa do agrupamento, com k ≤ n.
O Fatorial
Nos problemas de contagem é muito comum um tipo de problema em que, para se obter o resultado referente ao total das possibilidades, deve-se multiplicar um determinado número natural pelos seus antecedentes até chegar à unidade.
Para facilitar a obtenção desses resultados, as calculadoras (consideradas científicas) vêm com uma tecla conhecida como fatorial de n, que significa produto do número natural n pelos seus antecedentes até chegar à unidade.
Considere n um número inteiro não negativo. O fatorial de n, indicado por n!, é definido como sendo a seguinte multiplicação: $$n! = n · (n-1) · (n-2) · … · 3 · 2 · 1$$
Princípio Fundamental da Contagem
Se determinado acontecimento ocorre em etapas independentes, e se a primeira etapa pode ocorrer de k_1 maneiras diferentes, a segunda de k_2 maneiras diferentes, e assim sucessivamente, então o número total T de maneiras de ocorrer o acontecimento, composto por n etapas, é dado por:
$$T = k_1 k_2 k_3 … k_n.$$
O princípio fundamental da contagem nos diz que sempre devemos multiplicar os números de opções entre as escolhas que podemos fazer
EXEMPLO
Para montar um computador, temos 3 diferentes tipos de monitores, 4 tipos de teclados e 3 tipos de “CPU”. Para saber o numero de diferentes possibilidades de computadores que podem ser montados com essas peças, somente multiplicamos as opções:
3 (monitores) x 4 (teclados) x 3 (CPU)= 36
Então, têm-se 36 possibilidades de configurações diferentes.
EXEMPLO
Um restaurante oferece no cardápio 2 saladas distintas, 4 tipos de pratos de carne, 5 variedades de bebidas e 3 sobremesas diferentes. Uma pessoa deseja uma salada, um prato de carne, uma bebida e uma sobremesa. De quantas maneiras a pessoa poderá fazer seu pedido ?
a)90
b)100
c)110
d)130
e)120
Resposta: letra (e), pois, 2 (saladas) x 4 (carnes) x 5 (bebidas) x 3 (sobremesas) = 120.
EXEMPLO
Temos 3 cidades UBA, UDI, e ARI. Existem quatro rodovias que ligam UBA com UDI e cinco que ligam UDI com ARI. Partindo de UBA e passando por UDI, de quantas formas podemos chegar até ARI?
Resposta: 4 x 5 = 20.
EXEMPLO
Quatro atletas participam de uma corrida. Quantos resultados existem para o primeiro, segundo e terceiro lugares?
Resposta: 4x3x2x1=24
Diagrama de Árvore
O Diagrama da Árvore é um digrama que tem por objetivo visualizar as diversas opções da contagem de um acontecimento, é um método direto de contagem.
EXEMPLO
Um restaurante oferece no cardápio 2 saladas distintas, 4 tipos de pratos de carne. Uma pessoa deseja uma salada, um prato de carne. De quantas maneiras a pessoa poderá fazer seu pedido?
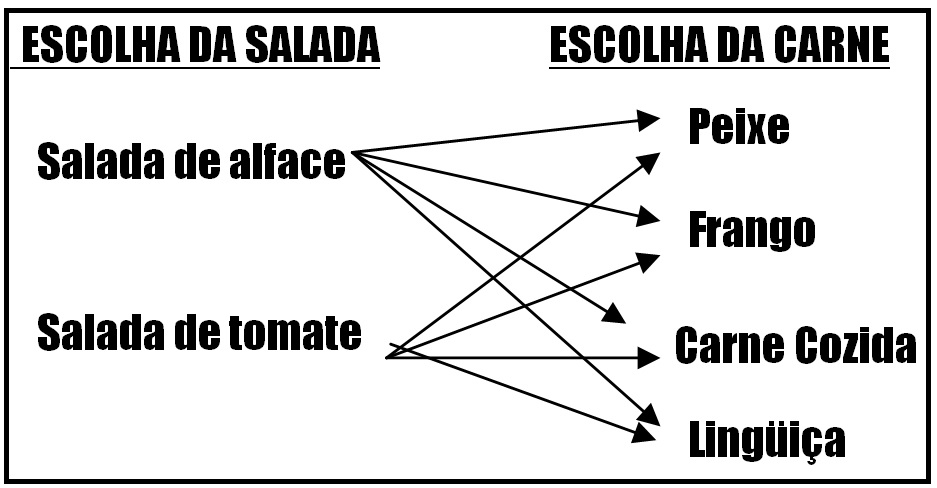
Resposta: 8 possibilidades diferentes.
EXEMPLO
Exemplo 2 João e Paulo disputam entre si um campeonato de xadrez com as seguintes regras:
I – vence a disputa quem ganhar duas partidas seguidas ou três em qualquer ordem.
II – em caso de empate, o vencedor será declarado através sorteio.
O número de resultados possíveis nesta competição é:
A) 10
B) 11
C) 12
D) 13
E) 15
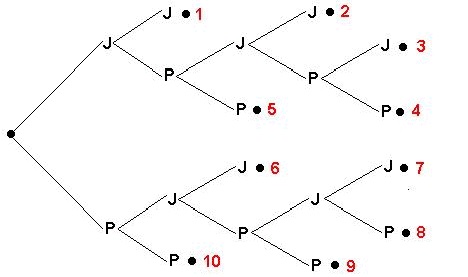
Resposta: Seja J a vitória de João e P a vitória de Paulo. Verificamos que são dez os resultados possíveis pelo diagrama de árvore.
OBSERVAÇÃO
Algumas vezes, o conjunto cujo elementos queremos contar consta de sequências de tamanhos diferentes, o que impede o uso do PFC.
Entretanto, usando o diagrama de árvore, podemos saber facilmente quantas são as sequências.
O PFC fornece-nos o instrumento básico para a Analise Combinatória, entretanto sua aplicação direta na resolução de problemas pode as vezes tornar-se trabalhosa.
Iremos então definir os vários modos de formamos agrupamentos.
Princípio Aditivo da Contagem
Toda vez que se deseja tomar uma decisão “E” logo após, outra, multiplica-se as parcelas.
Um exemplo desse problema é: uma pessoa deseja tomar um copo de suco e um refrigerante. Sabendo que há 5 tipos diferentes de sucos e 3 de refrigerantes, de quantas maneiras ele pode tomar esta decisão? (Resposta: 5×3=15)
Toda vez que se deseja tomar uma decisão OU outra, soma-se as parcelas.
Um exemplo desse problema é: uma pessoa deseja tomar um copo de suco ou um refrigerante. Sabendo que há 5 tipos diferentes de sucos e 3 de refrigerantes, de quantas maneiras ele pode tomar esta decisão? (Resposta: 5+3=8)
Isso vem do Princípio Aditivo da Contagem, que resolve situações de contagem, em que adicionamos as possibilidades.
Arranjos Simples
Temos um Arranjo quando os agrupamentos conseguidos ficam diferentes ao se inverter a posição dos seus elementos, desta forma, Arranjos são agrupamentos ordenados.
Seja N um conjunto com n elementos, isto é, N = \{ a_1, a_2, a_3,..., a_n\}.
Chamamos de arranjos dos n elementos, tomados p a p (1\leq p \leq N)a qualquer p-upla (sequencia de p elementos) formada com elementos de N todos distintos.
A fórmula do arranjo é dada por: $$A_{n,p} = \frac{n!}{(n-p)!}.$$
EXEMPLO
Queremos formar centenas de algarismos distintos, utilizando apenas os 5 primeiros números ímpares. De quantas formas podemos fazer isso?
Temos um arranjo de 5 números (1; 3; 5; 7; 9) em grupos de três (centenas).
$$A_{5,3} = \frac{5!}{(5-3)!} = \frac{5!}{2!} = 5 \times 4 \times 3 = 60$$
EXEMPLO
Em um estádio há 12 portas de entrada. Quantas chances você tem de entrar por uma porta e sair por outra?
$$A_{12,2} = \frac{12!}{(12-2)!} = \frac{12!}{10!} = 12 \times 11 = 132 $$
EXEMPLO
Quantos ímpares de quatro algarismos distintos podemos formar com os números 2, 4, 6, 7, 8 e 9, de tal maneira que os mesmos estejam entre 8000 e 10000?
Resposta:(possibilidade de ser 8 e 9)X(arranjo de 6, tomados 3 a 3)x (possibilidade de ser 7 ou 9). Achamos:
$$4 \times A_{6,3} =4 \times \frac{6!}{(6-3)!} = 4 \times \frac{6!}{3!} = 4 \times 6 \times 5 \times 4= 480$$
Permutação
Permutar significa trocar e, matematicamente, uma permutação é um caso particular de arranjo simples. É o tipo de agrupamento ordenado onde entram todos os elementos.
Seja N um conjunto com n elementos, isto é, N = \{ a_1, a_2, a_3,..., a_n\}.
Chamamos de permutação dos n elementos a todo arranjo em que p = n.
A fórmula do arranjo é dada por: $$P_n = A_{n,n} = \frac{n!}{(n-n)!} = \frac{n!}{0!} = n!$$
PERMUTAÇÃO COM REPETIÇÕES
Se entre os n elementos de um conjunto existem a elementos repetidos, b elementos repetidos, c elementos repetidos e assim sucessivamente, o número total de permutações que podemos formar é dado por:
$$P_n^{a,b,c…} = \frac{n!}{a!b!c!…}.$$
PERMUTAÇÃO CIRCULAR
Existe um tipo de permutação denominada circular, em que os elementos são dispostos em círculos ou ao redor de uma mesa circular.
Por exemplo, vamos colocar três objetos A, B, e C, distintos em 3 lugares numa circunferência.
Sendo (PC)_3 o número de permutações circulares de três elementos temos que: $$(PC)_3 = 2!$$
EXEMPLO
Quantos agrupamentos podemos formar com as vogais de nosso alfabeto?
$$P_5 = A_{5,5} = 5! = 120$$
EXEMPLO
Denomina-se ANAGRAMA o agrupamento formado pelas letras de uma palavra, que podem ter ou não significado na linguagem comum. Calcule o número de anagramas da palavra MUNDIAL.
$$P_7 = A_{7,7} = 7! = 5040$$
EXEMPLO
Quantos são os anagramas da palavra BATATA?
Essa é uma permutação com repetição (3 letras A e 2 letras T):
$$P_6^{2,3} = \frac{6!}{2!3!} = \frac{6 \times 5 \times 4 \times 3!}{3! 2!} = 6 \times 5 \times 2 = 60 $$
EXEMPLO
Uma família é composta por seis pessoas: o pai, a mãe e quatro filhos. Num restaurante, essa família vai ocupar uma mesa redonda. Em quantas disposições diferentes essas pessoas podem se sentar em torno da mesa de modo que o pai e a mãe fiquem juntos?
Resposta: Sabendo que pai e mãe devem ficar juntos, vamos amarrar os dois e tratá-los como se fossem um único elemento.
Ao tratar o pai e mãe como um único elemento, passamos a ter somente 5 elementos.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Portanto, utilizando a permutação circular de 5 elementos, calculamos o número de possibilidades desta família sentar-se ao redor da mesa com pai e mãe juntos sendo que o pai está à esquerda da mãe.
Permutação circular (PC)_5 elementos calcula-se: $$ (PC)_5 = P_4 = (5-1)! = 4! = 4.3.2.1 = 24.$$
Portanto, para o pai à esquerda da mãe, temos 24 posições diferentes. Mas o pai pode estar à direita da mãe, como na figura 2, e então teremos mais 24 posições diferentes para contar.
Portanto, o número total de disposições é 48.
EXEMPLO
Dois meninos e três meninas formarão uma roda dando-se as mãos. De quantos modos diferentes poderão formar a roda de modo que os dois meninos não fiquem juntos?
Resposta: No total temos 5 elementos para dispor em círculo, ou seja, novamente utilizaremos Permutação Circular.
Mas agora a restrição é diferente, os dois meninos NÃO podem ficar juntos.
Para esta situação, iremos calcular o número total de disposições (sem restrição) e diminuir deste resultado o número de disposições em que os meninos estão juntos (para calcular o número de disposições deles juntos, fazemos como no exercício anterior).
O número total de disposições é $$ (PC)_5 = P_4 = (5-1)! = 4! = 4.3.2.1 = 24.$$
Agora, para calcular o número de disposições com os meninos juntos, devemos amarrá-los e tratá-los como um único elemento, lembrando que podemos ter duas situações.
O número total de disposições com os meninos juntos é 2 \times (PC)_4 (4 elementos pois os meninos estão juntos e valem por 1).
Calculando este valor: $$ 2 \times (PC)_4 = 2.(4-1)! = 2.3! = 2.3.2.1 = 12.$$
Portanto, o número de disposições em que os meninos não estão juntos é 24-12=12.
Combinação
Temos uma combinação quando os agrupamentos conseguidos permanecem iguais ao se inverter a posição dos seus elementos(a ordem em que os elementos ocupam no grupo não tem importância).
Perceba que se houver cinco pessoas(João, Pedro, Luís, Gilberto e Ana) , entre as quais desejamos formar grupos de três, o grupo formado por João, Pedro e Luís é o mesmo grupo formado por Luís, Pedro e João. Temos, então, uma COMBINAÇÃO de cinco elementos em grupos de três.
Seja N um conjunto com n elementos, isto é, N = \{ a_1, a_2, a_3,..., a_n\}.
Chamamos de combinação dos n elementos, tomados p a p aos subconjuntos de N constituídos de p elementos.
Observe que a combinação é um conjunto, portanto não depende da ordem dos elementos. Quando calculamos o número de combinações de n objetos tomados p a p, estamos calculando o número de maneiras de “escolher” p objetos de um agrupamento de n objetos.
Como são subconjuntos de um conjunto, a ordem dos elementos não importa. Só consideramos subconjuntos distintos os que diferem pela natureza dos seus elementos.
A fórmula da combinação é dada por: $$C_{n,p} = \frac{n!}{p! (n-p)!}. $$
EXEMPLO
Um grupo consta de 30 pessoas, das quais 12 são filósofos. De quantas maneiras podemos formar comissões de 14 pessoas de modo que nenhum membro seja filósofo?
Das trinta pessoas, 18 não são filósofos. Desta forma, queremos escolher 14 pessoas entre 18:
$$C_{18,14} = \frac{18!}{14! 4!}= 3060.$$
EXEMPLO
Deseja-se formar comissões de 3 membros e dispõe-se de 10 funcionários. Quantas comissões podem ser formadas?
$$C_{10,3} = \frac{10!}{3! 7!}= 10 \times 3 \times 4 = 120.$$
EXEMPLO
Uma prova consta de 15 questões das quais o aluno deve resolver 10. De quantas formas ele poderá escolher as 10 questões?
$$C_{15,10} = \frac{15!}{10! 5!}= 3003.$$
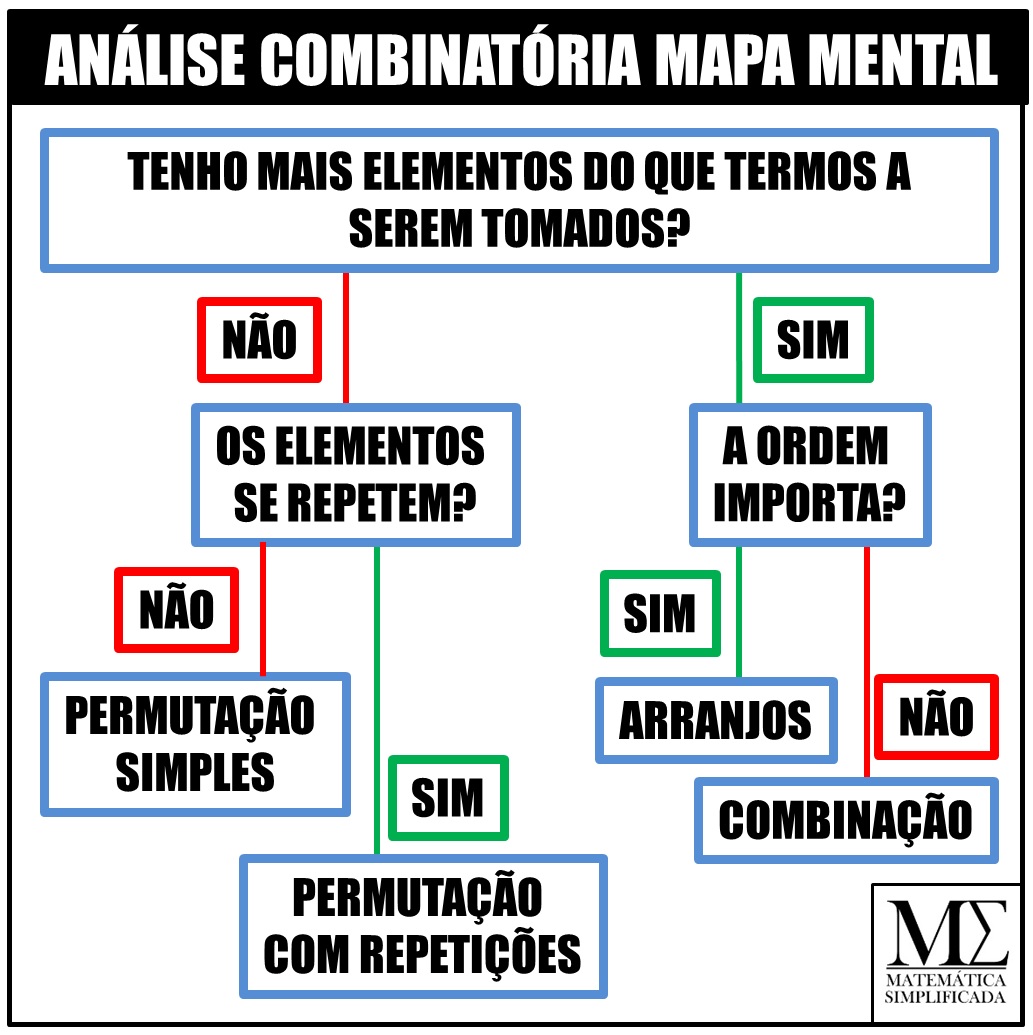
COMO USAR AS FÓRMULAS DA ANÁLISE COMBINATÓRIA?
O uso das fórmulas segue o seguinte mapa mental: