Por Que Você Não Entende Cálculo Diferencial e Integral? Explorando Dificuldades e Conceitos Fundamentais

Entendendo o Cálculo: Por Que Ele É Tão Temido e Como Entender os Conceitos Que Assustam 70% dos Estudantes Universitários?

Introdução

O cálculo não é apenas uma disciplina acadêmica; ele é uma linguagem que nos permite compreender e resolver problemas complexos do mundo real. Com aplicações que vão da engenharia ao design, da medicina à economia, o cálculo é a base para muitas das inovações que moldam nossas vidas.

Neste artigo, vamos desmistificar o cálculo, mostrando como ele pode ser aprendido e aplicado. Além disso, apresentaremos o Curso de Cálculo Completo, uma ferramenta prática e acessível para quem deseja dominar essa disciplina essencial.

Por Que o Cálculo Intimida Tanto?

Quando ouvimos falar de cálculo pela primeira vez, a reação comum é de medo. Isso acontece porque o cálculo é muitas vezes apresentado como um “novo idioma”, cheio de símbolos, regras complexas e conceitos abstratos que parecem distantes do mundo real.

Mas será que isso é verdade? Vamos explorar as causas dessa intimidação e como superá-la.

O primeiro fator que causa esse bloqueio é a transição entre a matemática básica e o cálculo. Durante o ensino médio, aprendemos álgebra, geometria e trigonometria, disciplinas que lidam com figuras regulares, fórmulas simples e aplicações visíveis.

Quando o cálculo aparece, ele introduz conceitos como limites, derivadas e integrais, que exigem um salto lógico para além do que estamos acostumados. Por exemplo, a ideia de somar infinitas partes pequenas para calcular a área total de uma figura irregular pode parecer abstrata, mas é isso que o cálculo faz.

Outro ponto crítico é o método de ensino. Em muitas escolas e universidades, o cálculo é ensinado de forma teórica e descontextualizada, com foco na memorização de fórmulas como
\[ \int_a^b f(x) \, dx \ = F(b)- F(a) \qquad \text{se  } f(x) = F'(x) \]
e na resolução mecânica de problemas. Isso impede que os alunos compreendam o “porquê” de cada operação, criando um bloqueio que leva muitos a desistirem da matéria.

Finalmente, a pressão acadêmica contribui para esse cenário. Disciplinas como Cálculo 1, 2 e 3 têm altos índices de reprovação porque exigem não apenas conhecimento técnico, mas também rapidez e precisão. Muitos alunos enfrentam provas difíceis, que cobram domínio de conceitos e técnicas que nem sempre foram bem explicados.

Mas há uma solução. Com o Curso de Cálculo Completo, você terá acesso a aulas práticas que conectam teoria e realidade. O curso aborda os fundamentos de forma simples e clara, ajudando você a superar as barreiras e a aprender cálculo de verdade.

O Papel do Cálculo na Educação e na Vida Prática

Segundo Feynman, um físico teórico norte-americano do século XX, o cálculo “é a língua falada por Deus”.

O cálculo desempenha um papel central na educação e em diversas áreas do mundo real. Ele não é apenas uma exigência curricular, mas uma ferramenta poderosa para resolver problemas complexos e criar soluções inovadoras.

Vamos explorar como o cálculo está inserido na formação acadêmica e no cotidiano.

O papel do cálculo no sistema educacional

No ensino médio, o cálculo é geralmente reservado para os currículos avançados, sendo estudado após disciplinas como álgebra, geometria e pré-cálculo.

Já no ensino superior, ele se torna indispensável em cursos como engenharia, economia, física e biologia. Essas áreas dependem do cálculo para analisar fenômenos, modelar comportamentos e fazer previsões.

Um dos principais desafios no ensino do cálculo é a falta de base sólida em matemática básica. Muitos alunos chegam à disciplina sem dominar conceitos fundamentais, como funções e trigonometria, o que torna a compreensão de tópicos como limites e derivadas ainda mais difícil. Por exemplo, entender
\[
\lim_{x \to 0} \frac{\sin x}{x} = 1
\]
exige uma noção clara do que é um limite.

O papel do cálculo no mundo real

Fora da sala de aula, o cálculo está presente em praticamente todas as áreas. Ele é usado para modelar fenômenos naturais, como o fluxo de fluidos em tubulações, o movimento dos planetas e até a propagação de epidemias. Na medicina, ele é essencial para criar exames de imagem, como tomografias e ressonâncias magnéticas, enquanto na engenharia, ele permite projetar estruturas seguras e eficientes.

Na economia, o cálculo ajuda a otimizar lucros, reduzir perdas e prever tendências de mercado. Em ciência de dados e inteligência artificial, ele é a base para algoritmos que processam informações e tomam decisões. Esses exemplos mostram como o cálculo vai muito além do papel e do quadro negro.

O Curso de Cálculo Completo prepara você para aplicar o cálculo em situações práticas, conectando teoria e realidade. Com uma abordagem acessível e exercícios reais, você estará pronto para usar o cálculo como uma ferramenta transformadora.

Os Dois Grandes Problemas Que o Cálculo Resolve

O cálculo resolve dois problemas fundamentais que estão na base de muitas aplicações práticas:

1. Determinar medidas de estruturas e formas complexas.
2. Identificar inclinações ou taxas de variação em curvas.

Esses problemas, aparentemente simples, têm implicações profundas em áreas como engenharia, física, economia e ciência de dados.

1. Medidas e Estruturas de formas complexas

A matemática básica nos dá fórmulas para calcular áreas simples, como \( \text{Comprimento} \times \text{Largura} \) para retângulos ou \( \pi r^2 \) para círculos. Mas o que acontece quando lidamos com formas irregulares? Por exemplo, como calcular a área de um lago com bordas sinuosas ou o volume de um objeto tridimensional com cavidades internas?

O cálculo resolve esse problema por meio das integrais. Imagine dividir a área de um lago em infinitas tiras muito finas e somar suas áreas. Essa ideia, representada pela integral
\[
\int_a^b f(x) \, dx,
\]
permite calcular áreas e volumes com precisão, algo indispensável na engenharia civil, na arquitetura e no design de produtos.

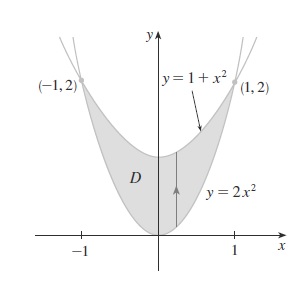Com o Cálculo podemos calcular áreas como a desta figura facilmente usando a integração definida

2. Inclinações e taxas de variação

Outro problema central do cálculo é determinar a inclinação de curvas ou a taxa de variação de uma função. As derivadas são semelhantes ao conceito algébrico de inclinação. Em álgebra, a inclinação de uma linha indica a taxa de variação de uma função linear, ou a quantidade que y aumenta com cada aumento de unidade em x.

O cálculo estende esse conceito para funções não lineares (ou seja, aquelas cujos gráficos não são linhas retas). Em outras palavras, permite encontrar a inclinação, ou taxa de aumento, das curvas.

O problema é que as inclinações dessas funções não lineares são diferentes em cada ponto ao longo da curva. Isso significa que a derivada de f(x) geralmente ainda é uma função.

Imagine um gráfico que mostra o crescimento populacional ou a variação do preço de uma ação. Saber a inclinação desse gráfico em um ponto específico ajuda a prever tendências e tomar decisões estratégicas.

As derivadas são a ferramenta do cálculo para lidar com esses problemas. Elas permitem calcular a inclinação exata de uma curva em qualquer ponto, como mostrado em
\[
\frac{df}{dx}(x) = \lim_{h \to 0} \frac{f(x+h) – f(x)}{h}.
\]
Essa técnica é usada em economia, medicina e física para modelar e prever comportamentos através das equações diferenciais.

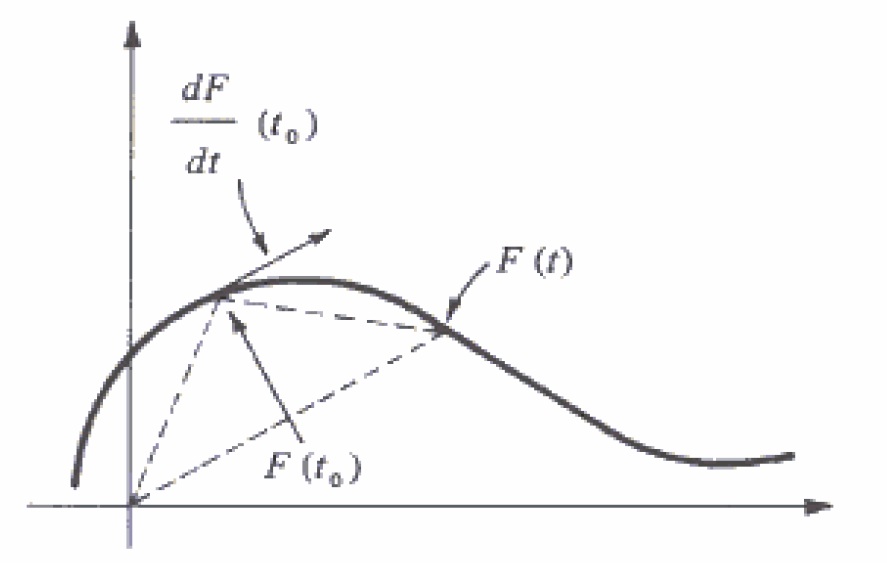Interpretação geométrica da derivada.

Essas equações (diferenciais) descrevem a diferença entre algo neste momento e no momento seguinte, ou entre uma coisa aqui e a mesma coisa em outro ponto infinitamente próximo.

Com o Curso de Cálculo Completo, você aprenderá a aplicar integrais e derivadas em problemas reais, dominando essas ferramentas essenciais.

Isso só é possível por causa do limite

Assim, o cálculo se desenvolve em duas partes: fatiamento e recomposição. Em termos matemáticos, o processo de fatiamento envolve uma subtração infinitamente leve, usada para quantificar as diferenças entre as partes. Essa primeira metade do processo é chamada de cálculo diferencial. O processo de reconstrução sempre envolve uma adição infinita, que reintegra as partes do todo original. Essa metade do processo é chamada de cálculo integral.

O que faz esses dois processos possíveis é um conceito matemático chamado limite. Os limites são uma parte fundamental do cálculo e estão entre as primeiras coisas que os alunos aprendem em uma aula de cálculo.

Um limite é como uma meta inatingível. Você pode se aproximar cada vez mais, porém nunca chegará lá.

Foram necessários cerca de 2 mil anos para que o conceito de limite fosse rigorosamente definido. Até então, os pioneiros do cálculo se arranjavam muito bem usando a própria intuição.

Sob uma perspectiva moderna, ele são importantes porque constituem os alicerces sobre os quais o cálculo foi construído.

Um exemplo simples: Os três pontos no final da série 0,333… têm duas interpretações. A interpretação ingênua é que existem infinitos números 3 agrupados lado a lado à direita da vírgula decimal. A interpretação mais sofisticada é a de que 0,333… representa o limite da fração 1/3. Ou ainda o valor da soma infinita 3/10+3/100+3/1000+…

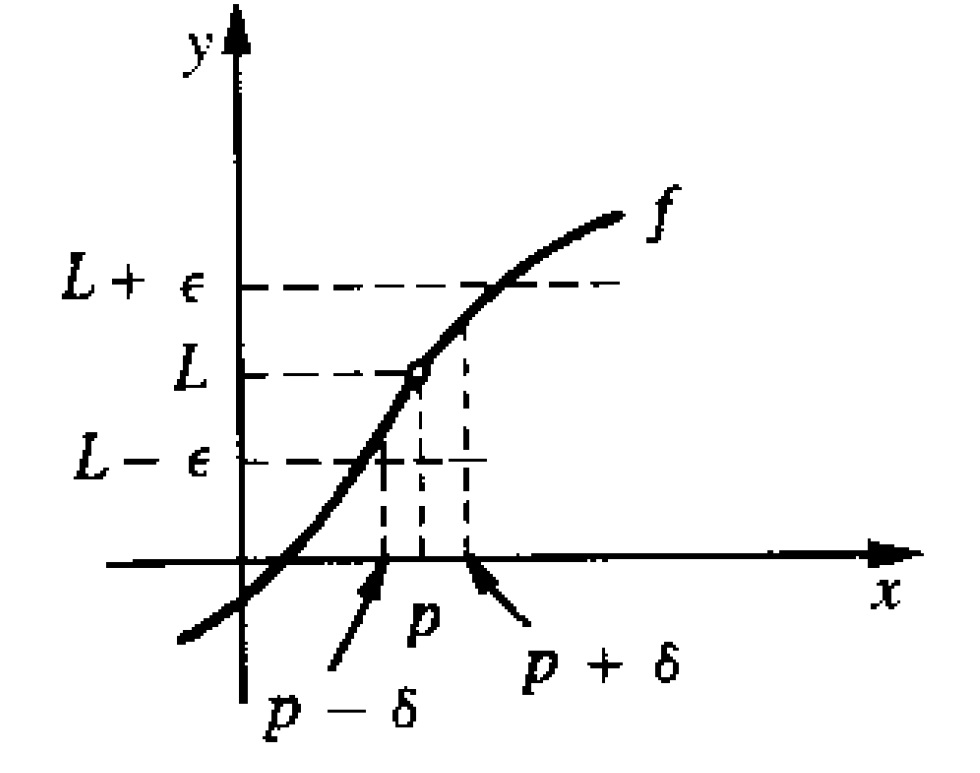
A Chave do Cálculo

1. Os limites predizem o valor de uma função em um determinado ponto qu epode, ou não, estar no domínio dela.
2. As derivadas são funções que fornecem a taxa de variação de uma função.
3. As integrais definidas calculam a área. As integrais indefinidas são o oposto das derivadas. Em outras palavras, derivar uma função e integrar uma função são operações opostas. Para “desfazer” uma derivada, basta integrá-la (e vice-versa).

Conclusão: O Cálculo Como Ferramenta Transformadora

O cálculo é muito mais do que uma disciplina acadêmica; ele é uma linguagem que conecta teoria e prática. Com ele, podemos resolver problemas complexos, criar inovações tecnológicas e entender melhor o mundo ao nosso redor.

Mesmo no domínio subatômico, onde a física de Newton perde a validade, o cálculo newtoniano ainda funciona. Aliás, funciona espetacularmente bem, unindo-se à mecânica quântica para prever os notáveis efeitos subjacentes aos diagnósticos por imagem, desde a ressonância magnética e a tomografia computadorizada até a esdrúxula tomografia por emissão de pósitrons.

Apesar de seu aspecto intimidador, o cálculo é acessível a qualquer pessoa disposta a aprender.

Se você quer dominar essa matéria e transformá-la em um diferencial na sua carreira, o Curso de Cálculo Completo é a solução ideal. Com aulas claras, suporte dedicado e exercícios práticos, você estará pronto para enfrentar qualquer desafio. Inscreva-se agora e transforme sua relação com o cálculo.

Por Que é tão Difícil Passar em Cálculo?

Se você chegou até aqui, provavelmente já enfrentou ou está enfrentando dificuldades com cálculo. Não se preocupe, você não está sozinho. A verdade é que o cálculo é uma disciplina que intimida muitos estudantes, e isso não acontece por acaso. Vamos explorar os principais motivos que tornam essa matéria tão desafiadora.

1. A Falta de Fundamentos Sólidos

O aprendizado do cálculo exige uma base sólida em álgebra, trigonometria e outras áreas da matemática básica. Infelizmente, muitos alunos chegam ao cálculo sem dominar esses conceitos fundamentais. Isso é como tentar construir uma casa sem alicerces: o progresso se torna instável e confuso.

2. O Volume de Conteúdo

Abrir um livro de cálculo pela primeira vez pode ser assustador. Cada página parece trazer uma fórmula nova, cheia de símbolos desconhecidos. Essa avalanche de informações intimida e faz o cálculo parecer impossível. No entanto, o que poucos percebem é que a maioria dessas fórmulas segue padrões repetitivos que podem ser identificados e aprendidos com o tempo.

3. A Pressão Acadêmica

Disciplinas como Cálculo 1, 2 e 3 são conhecidas pelo alto índice de reprovação. Provas desafiadoras, pouco tempo para preparação e a falta de compreensão profunda dos conceitos levam muitos estudantes ao famoso “branco”. Isso cria uma relação de medo com a matéria, dificultando ainda mais o aprendizado.

Apesar desses desafios, o cálculo não é um monstro intransponível. Ele é baseado em regras claras e, quando bem apresentado, pode ser entendido por qualquer pessoa.

Uma Solução Para o Seu Problema: Curso de Cálculo Completo

Agora que entendemos por que o cálculo parece tão difícil, é hora de falar sobre como você pode superar essas barreiras. O Curso de Cálculo Completo foi criado para ajudar estudantes exatamente como você, que enfrentam dificuldades em Cálculo 1, 2 e 3. Com uma abordagem prática e didática, o curso torna o aprendizado do cálculo acessível e eficiente.

O Que o Curso Oferece?

1. Conteúdo Abrangente: Do básico ao avançado, cobrindo limites, derivadas e integrais.
2. Aulas Didáticas: Explicações claras e objetivas para facilitar o entendimento.
3. Exercícios Práticos: Resolução passo a passo de problemas reais.
4. Suporte Personalizado: Ajuda individual para esclarecer dúvidas.

Os Benefícios de Participar

1. Flexibilidade: Estude no seu ritmo, com acesso ilimitado ao conteúdo.
2. Preparação para Provas: Conquiste confiança para encarar Cálculo 1, 2 e 3.
3. Aplicação Prática: Use o que aprendeu para avançar na sua carreira acadêmica e profissional.

Imagine Superar o Cálculo Com Tranquilidade

Pense em como seria enfrentar as disciplinas de cálculo sem medo. Imagine passar pelas provas com confiança, entender os conceitos fundamentais e finalmente deixar para trás a sensação de frustração. Com o Curso de Cálculo Completo, isso é possível.

Aproveite esta oportunidade única para transformar sua relação com o cálculo. Clique no link abaixo ou escaneie o QR Code para se inscrever agora. Não deixe essa chance passar – o sucesso está ao seu alcance.

Clique no banner abaixo e inscreva-se agora no Curso de Cálculo Completo

Leia Mais:

• Os 5 Melhores Livros Para Estudar Cálculo Diferencial e Integral
• O melhor livro de Pré Cálculo: O Guia completo até para leigos
• Como Aprender Matemática Sozinho? As Melhores Técnicas de Estudo
• Equações Diferenciais: Os 5 Melhores Livros para Aprender Sozinho
• 16 Exercícios Resolvidos Sobre Integrais para Estudantes de Engenharia