Curioso sobre as Pontes Königsberg? Descubra o enigma matemático e entenda como o grande matemático Leonard Euler decifrou-o.
As Pontes de Königsberg há muito fascinam matemáticos e entusiastas de quebra-cabeças. Essas estruturas icônicas na cidade de Königsberg, agora conhecida como Kaliningrado, na Rússia, representam um desafio matemático que levou séculos para ser resolvido. Descubra a intrigante história por trás das Pontes Königsberg e como o grande matemático Leonard Euler finalmente decifrou o código.
Às vezes, um simples quebra-cabeça inicia todo um novo campo na matemática. Tais acontecimentos são raros, mas consigo me lembrar de ao menos três. O mais famoso deles é conhecido como As Pontes de Königsberg, que levou Leonhard Euler (pronuncia “Óiler”, e não “Êuler”) a inventar um ramo da teoria dos grafos, em 1735.
Königsberg, que naquele tempo ficava na Prússia, é cortada pelo rio Pregelarme. Havia duas ilhas, ligadas às margens e en tre elas próprias por 7 pontes. A pergunta que os moradores se faziam: seria possível a um caminhante dar um passeio de forma a passar em cada uma das sete pontes uma – e apenas uma vez?
Por tentativa e erro, as pessoas se convenceram de que o passeio era impossível. Mas como provar isso matematicamente?
 Oferta: “Almanaque das Curiosidades Matemáticas”, de Ian Stewart, com 20% de desconto
Oferta: “Almanaque das Curiosidades Matemáticas”, de Ian Stewart, com 20% de desconto
As Sete Pontes de Königsberg.
As Sete Pontes de Königsberg é um famoso problema matemático que intrigou os matemáticos durante séculos. O problema envolvia encontrar uma rota pela cidade de Königsberg que cruzasse cada uma de suas sete pontes exatamente uma vez e retornasse ao ponto de partida.
Este é um problema elementar da matemática que muitos tentaram resolver antes de Euler, mas foi apenas no século 18 que o matemático suíço Leonhard Euler finalmente decifrou o código.
A solução de Euler lançou as bases para a teoria dos grafos, um ramo da matemática que desde então tem sido aplicado a vários campos, incluindo ciência da computação e planejamento de transporte, telecomunicações, tráfego de veículos, projeto de chips, biologia etc.
Quem foi Leonhard Euler?
Leonhard Euler foi o matemático mais prolífico de todos os tempos. Nasceu em 1707 em Basileia, na Suíça, e morreu em 1783, em São Petersburgo, na Rússia. Escreveu mais de 800 artigos científicos e uma longa lista de livros.
Euler teve 13 filhos e muitas vezes trabalhou em sua matemática com um dos filhos sentado no colo. Perdeu a visão de um olho em 1735, provavelmente em virtude de catarata, e a do outro em 1766. A cegueira aparentemente não afetou em nada sua produtividade.
Sua família fazia anotações, e ele tinha uma incrível capacidade mental – certa vez, fez um cálculo com 50 casas decimais para decidir qual de seus dois alunos estava certo.
Euler passou muitos anos na corte da Rainha Catarina, a Grande. Conta-se que, para não se meter nos imbróglios políticos da corte que poderiam facilmente se mostrar fatais, ele passava quase todo o tempo trabalhando na matemática, só parando para dormir.
Dessa forma, é claro que não sobraria muito tempo para fazer intriga.
 Oferta: Livro As Pontes de Konigsberg, de David Toscana
Oferta: Livro As Pontes de Konigsberg, de David Toscana
A Solução de Euler: O Nascimento da Teoria dos Grafos.
A solução de Leonhard Euler para o problema das Pontes de Königsberg marcou um marco significativo no campo da matemática. Euler percebeu que a chave para resolver o problema estava em abstrair o layout da cidade em uma estrutura matemática conhecida como gráfico.
Euler resolveu o problema provando não existir nenhuma solução. Em termos mais gerais, ele apresentou um critério para que qualquer problema do gênero tenha uma solução e observou que o critério não se aplicava àquele exemplo em particular.
Euler percebeu que a geometria exata é irrelevante – o que importa é a forma como as coisas estão inter- ligadas. Assim, o problema se reduz a uma simples rede de pontos uni- dos por linhas, mostrados aqui em sobreposição ao mapa.
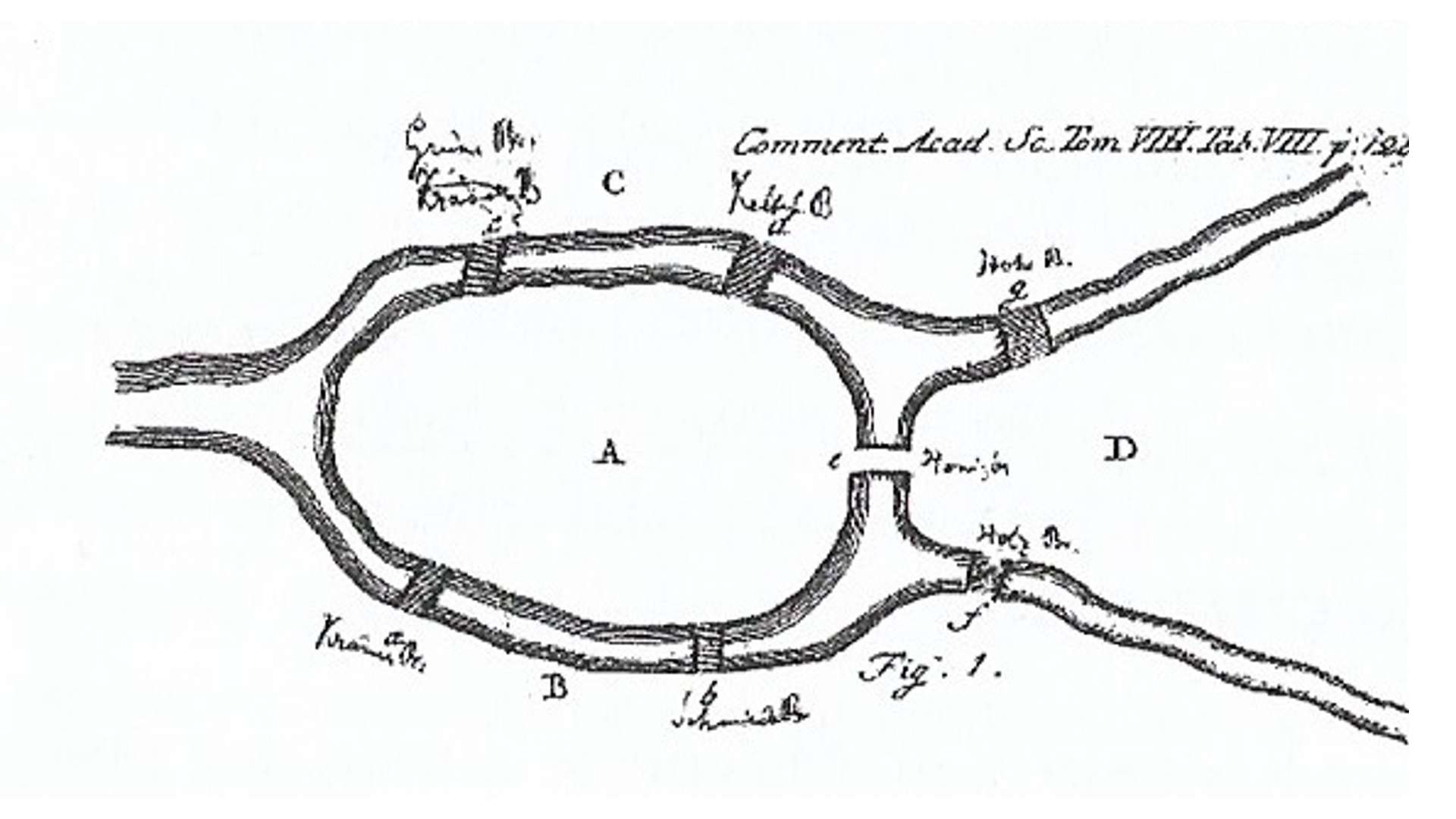 O desenho das pontes de Königsberg feito por Euler.
O desenho das pontes de Königsberg feito por Euler.
Cada ponto corresponde a uma porção de terra, e dois pontos estão unidos por linhas se houver uma ponte ligando as porções de terra correspondentes.
Ao representar as massas de terra como nós e as pontes como arestas que as conectam, Euler foi capaz de formular um conjunto de regras que determinariam se uma rota pela cidade era possível.
Essa abordagem inovadora lançou as bases para a teoria dos grafos, que desde então se tornou uma ferramenta fundamental em vários campos, incluindo ciência da computação, planejamento de transporte e análise de redes.
A solução de Euler para o problema das Pontes de Königsberg continua sendo uma prova do poder do pensamento matemático e de sua capacidade de resolver enigmas do mundo real.
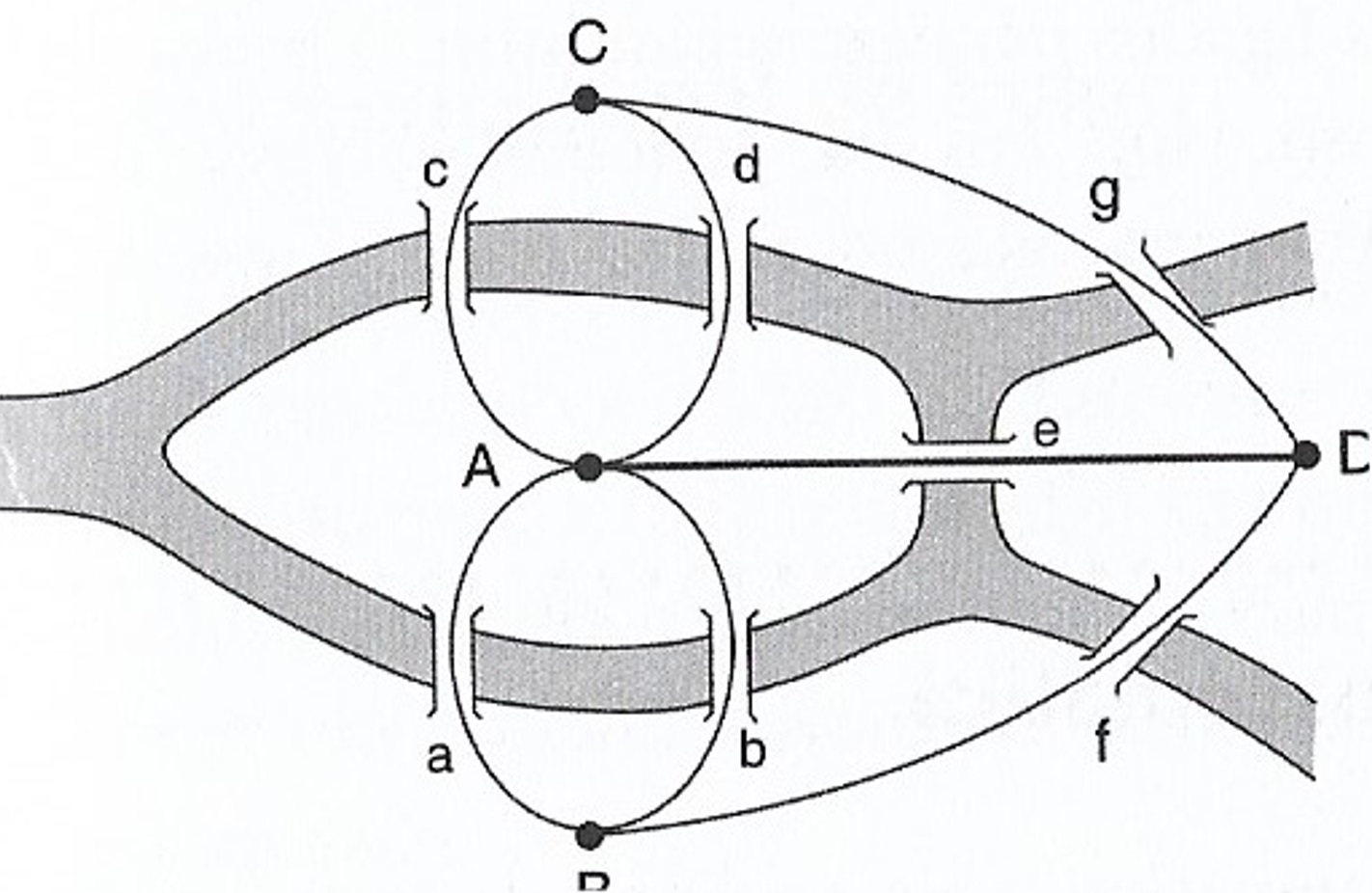 Transformando as pontes de Konigsberg numa rede
Transformando as pontes de Konigsberg numa rede
Assim, temos 4 pontos, A, B, C e D, e 7 arestas, a, b, c, d, e, f, g, uma para cada ponte. Podemos agora simplificar o problema para o seguinte: será possível encontrar um trajeto que atravesse a rede passando por cada aresta exatamente uma vez?
Você talvez queira tentar antes de continuar a leitura.
Para descobrir se tais problemas têm solução ou não, Euler distinguiu dois tipos de trajeto. Um caminho aberto começa e termina em pontos diferentes; um caminho fechado começa e termina no mesmo ponto.
Ele provou que, nesta rede em particular, nenhum dos dois tipos de caminho é possível. A principal ideia teórica é a da valência de cada ponto, ou seja, quantas linhas se encontram ali. Por exemplo, 5 linhas se encontram no ponto A, portanto a valência de A é 5.
Suponha que exista um caminho fechado em alguma rede. Sempre que uma das linhas de um caminho entra em um ponto, a linha seguinte deverá sair desse ponto. Portanto, se for possível econtrar um caminho fechado, o número de linhas de cada ponto deverá ser par: todos os pontos deverão ter a mesma valência.
Isso já descarta qualquer caminho fechado pelas Pontes de Königsberg, porque essa rede tem 3 pontos de valência 3 e 1 ponto de valência 5 – que são todos números ímpares.
Um critério semelhante funciona com caminhos abertos, mas nesse caso deverá haver exatamente 2 pontos com valência ímpar: um no início do caminho, outro ao final. O diagrama de Königsberg tem 4 vértices de valência ímpar, portanto tampouco poderemos encontrar um caminho aberto.
Euler também provou que essas condições são suficientes para que exista um caminho, desde que o diagrama esteja conectado quaisquer 2 pontos devem estar ligados por algum caminho.
A prova de Euler para isso é bastante extensa. Hoje em dia, podemos escrever uma prova para isso em poucas linhas, graças a novas descobertas inspiradas em seus esforços pioneiros.
A importância do Problema das Pontes de Königsberg para a matemática.
O problema das Pontes de Königsberg destaca a importância da conectividade na matemática. A solução de Euler demonstrou que entender as relações e conexões entre diferentes elementos pode levar à solução de problemas complexos.
No caso das pontes Königsberg, foram as conexões entre as massas de terra e as pontes que continham a chave para encontrar uma solução. Este conceito de conectividade não se limita apenas à matemática.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Pode ser aplicado a vários campos e disciplinas, enfatizando a importância de entender como diferentes componentes interagem e se influenciam. Seja analisando redes, projetando sistemas de transporte eficientes ou resolvendo quebra-cabeças logísticos, reconhecer e utilizar a conectividade é essencial para a solução de problemas e inovação.
O Legado das Pontes Königsberg.
O problema das Pontes de Königsberg, proposto pela primeira vez no século 18 pelo matemático suíço Leonhard Euler, deixou um legado duradouro no campo da matemática. A solução de Euler para o problema não apenas revolucionou a teoria dos grafos, mas também lançou as bases para o campo da topologia.
Ao abstrair o problema em uma estrutura matemática, Euler conseguiu provar que era impossível encontrar um caminho que cruzasse cada uma das sete pontes em Königsberg exatamente uma vez.
Esta solução inovadora abriu caminho para o desenvolvimento da teoria dos grafos moderna e teve implicações de longo alcance em vários campos de estudo. Hoje, o problema das Pontes de Königsberg continua sendo estudado e serve como exemplo fundamental em cursos de teoria dos grafos ao redor do mundo.
Do problema das pontes de Königsberg derivou-se o problema do caixeiro-viajante: Se você tem um mapa de cidades com as estradas que fazem a ligação entre elas, será possível achar um caminho que passe em cada cidade apenas uma vez e volte à cidade inicial?
O problema das Pontes de Königsberg traz esse mesmo desafio para sete pontos, mas agora imagine que você precisa de uma solução que funcione para todos os mapas, independente da quantidade de pontos.
É um problema gigantesco a ser considerado e a classe desses problemas impraticáveis é denominada problemas polinomiais não-determinísticos ou simplesmente pela sigla NP.
Esse tipo de problema rege a solução genérica para todos os jogos tipo “caça-mina” presente no software Windows, por exemplo.
O mais intrigante é que se for encontrado um método simples de resolver um problema NP, ele poderá ser aplicado a todos e assim seria provada a fórmula NP=P.
Hoje a ciência lida com milhares de problemas com essa natureza e resolve-los significaria um salto gigantesco na ciência moderna. Este é um dos problemas modernos da matemática cuja solução dará um prêmio de 1 milhão de dólares.
 Oferta: Livro “O poder do infinito: Como o cálculo revela os segredos do universo”, de Steven Strogatz, com 20% de desconto.
Oferta: Livro “O poder do infinito: Como o cálculo revela os segredos do universo”, de Steven Strogatz, com 20% de desconto.

