Os Espaços Euclidianos R² e R³ | 2ª Lista de Exercícios Resolvidos

O Espaço euclidiano é um espaço em qualquer número finito de dimensões, no qual os pontos são designados por coordenadas (uma para cada dimensão) e a distância entre dois pontos é dada por uma fórmula de distância.

O espaço euclidiano n-dimensional é o produto cartesiano de n fatores iguais a \mathbb{R}. Ou seja,

1.  \mathbb{R}^2 = \mathbb{R} \times \mathbb{R}. Pode ser geometricamente representado pelo plano cartesiano.
2. \mathbb{R}^3 = \mathbb{R} \times \mathbb{R} \times \mathbb{R}. Pode ser geometricamente representado pelo eixo tridimensional.

Aqui queremos apresentar uma segunda lista de exercícios resolvidos envolvendo matemáticos objetos comuns a espaços euclidianos, como retas, planos e pontos e particularidades inerentes a estes conceitos.

Os Espaços Euclidianos R² e R³ – 2ª Lista de Exercícios Resolvidos

1. Mostre que a a equação $$4(x^2 +y^2+z^2+x-2y+2z) – 7 = 0$$ representa a superfície de uma esfera, ou seja, que todos os pontos que satisfazem essa equação possuem a mesma distância em relação a um ponto especifico do espaço.

SOLUÇÃO: Observe que por manipulações algébricas encontramos:

$$4(x^2 +y^2+z^2+x-2y+2z) – 7 = 0$$ $$x^2 +y^2+z^2+x-2y+2z = \frac{7}{4}$$ $$\left(x^2 + x + \frac{1}{4} \right)+ \left(y^2 -2y +1 \right)  + \left( z^2 +2z +1 \right) = \frac{7}{4} + \frac{1}{4} +1 +1$$ $$\left( x + \frac{1}{2} \right)^2 + \left( y-1 \right)^2 + \left( z + 1 \right)^2 = 4$$ $$\sqrt{\left( x + \frac{1}{2} \right)^2 + \left( y-1 \right)^2 + \left( z + 1 \right)^2} = 2,$$ ou seja, a distância de qualquer ponto (x,y,z) da superfície ao ponto \left( \frac{1}{2} , 1, -1 \right) é igual a 2.

Logo, a superfície é uma esfera com centro no ponto \left( \frac{1}{2} , 1, -1 \right) e raio igual a 2.

2. Determinar a equação geral do plano que contém as retas $$r:\left\{ \begin{array}{lll}
y & = &2x+1\\
z & = &-3x-2\\
\end{array} \right.
$$ e $$s:\left\{ \begin{array}{lll}
x & = & -1 +2t\\
y & = & 4t\\
z & = &3-6t\\
\end{array} \right.
$$

SOLUÇÃO: Observe que as duas retas são paralelas e tem vetores diretores dados, respectivamente, por $$ \vec{u} = (1,2,-3) \;\;\; e \;\;\;  \vec{v} = (2,4,-6). $$

Logo, precisamos construir um vetor \vec{w} que seja determinado por um ponto de cada reta: $$ \vec{w} = (-1,0,3) – (0,1,-2) = (-1,-2,5). $$

O vetor normal ao plano que queremos, então, é dado por $$ \vec{w} = \vec{u} \wedge \vec{v} = (1,2,-3) \wedge (-1,-2,5) = (7, -2, 1) .$$

Assim, a equação geral do plano que contém as retas é dada por: $$ \pi: 7x -2y +z +d = 0.$$

Usando o ponto da reta r, A(0,1,-2), que também precisará ser um ponto do plano, encontramos d = 4, ou seja $$ \pi: 7x -2y +z +4 = 0.$$

Para verificar que este realmente é o plano procurado, basta inserir as equações paramétricas de cada uma das retas na equação geral do plano e observar que a igualda se mantém verdadeira.

3. Encontre a equação da reta que passa pelo ponto (2,3) e é perpendicular à reta que passa pelo centro da circunferência de equação $$x^2+y^2+8x-4y+11=0$$ e pelo foco de coordenadas positivas da hipérbole de equação $$\frac{x^2}{64} – \frac{y^2}{36} =1.$$

SOLUÇÃO: A reta procurada no exercício é a destacada em verde na ilustração abaixo:

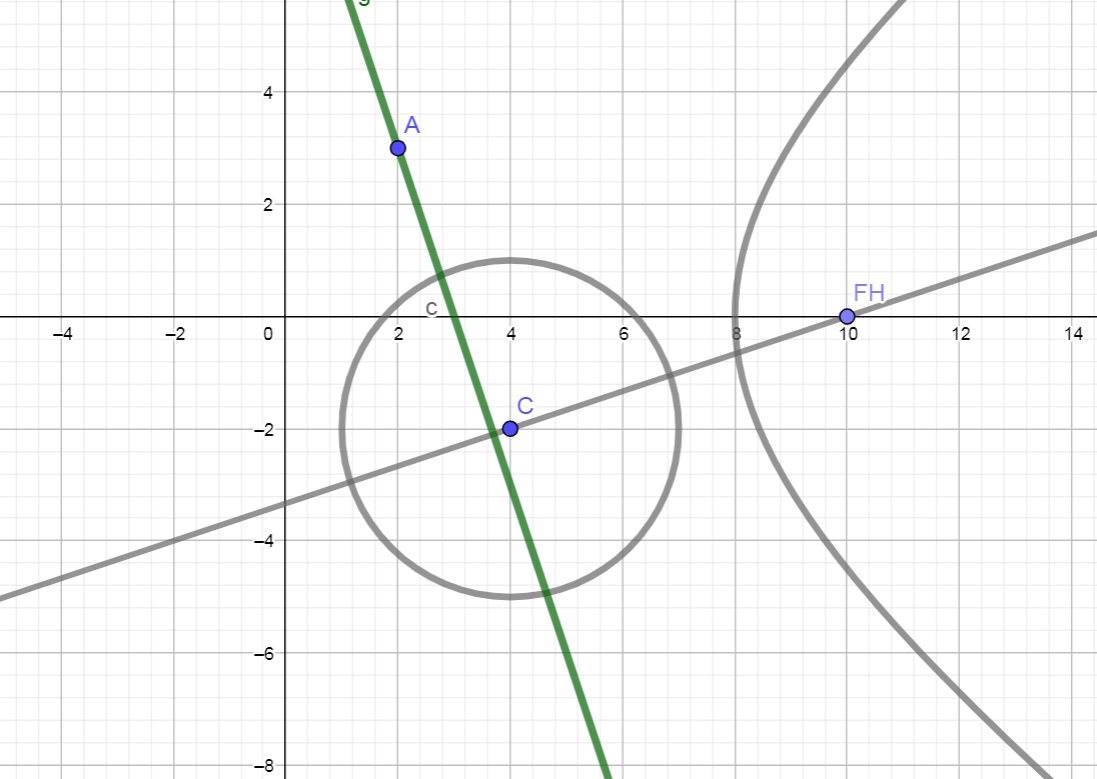
Por uma manipulação algébrica encontramos $$x^2+y^2+8x-4y+11=0 \Rightarrow \left(  x+4 \right) ^2 + \left( y-2 \right) ^2 = 3^2,$$ ou seja, temos uma circunferência com centro C(4,-2) e raio igual a 3.

Agora, olhando para a hipérbole  com equação $$\frac{x^2}{64} – \frac{y^2}{36} =1,$$ percebemos que ela é centrada na origem e com eixo real sobre o eixo Ox e de medida 2a = 16. Logo, os focos são dados por (c, 0) e (-c , 0), onde c^2 = a^2 + b^2 .

Desta forma, o foco de coordenadas positivas desta hipérbole é o ponto FH(10,0).

Assim, a equação da reta que passa pelo centro da circunferência e pelo foco de coordenadas positivas da hipérbole é dada por $$ r: (x,y) = (10,0) + t \left[ (10,0) – (4,-2) \right]  = (10,0) + t (6,2).$$

Queremos encontrar a reta s que passa pelo ponto (2,3) e é perpendicular à reta essa reta r.

Seja (x,y) um ponto genérico da reta s. Logo o vetor diretor desta reta é dada por \vec{u} = (x - 2,y - 3) .  Para que as retas sejam perpendiculares é necessário que $$ (x – 2,y – 3) . (6,2) = 0 \Rightarrow 6(x-2) + 2 (y-3) = 0 \Rightarrow 3x + y = 9. $$

Logo, o pontos da reta s devem satisfazer a igualdade $$y =9 -3x,$$ que é a equação geral da reta no plano xOy. As equação paramétricas desta reta são dada por $$s:\left\{ \begin{array}{lll}
x & = & t\\
y & = &-3t +9\\
\end{array} \right.
$$

Leia Mais:

• Os Espaços Euclidianos R² e R³ | Norma, Distância, Retas e Planos
  
• Os Espaços Euclidianos R² e R³ | 1ª Lista de Exercícios Resolvidos
• Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
• Curvas no Espaço | Funções de uma Variável Real a Valores Vetoriais