Guia Completo Sobre Números Racionais e Inteiros Relativos

Descubra tudo sobre números inteiros e racionais relativos, suas operações, propriedades e as nuances da desigualdade matemática.

Introdução

Exploramos o fascinante mundo dos números inteiros e racionais relativos. Este post detalha suas definições, operações básicas como adição, subtração, multiplicação e divisão, além de discutir suas propriedades e a relação de ordem entre eles. Se você está procurando entender como os números interagem em diferentes condições, este guia é perfeito para você.

Inteiros Relativos

Chamaremos de $\mathbb{Z}$ , o conjunto dos números inteiros relativos: $$\mathbb{Z} = {…, -3, -2, -1, 0, +1, +2, +3, …}$$

Com a criação do conjunto $\mathbb{Z}$ , a subtração se tornou uma operação possível, com os números inteiros, independentemente da ordem na qual eles figuram. Por exemplo,

$9 - 4 = 5 \in \mathbb{N}$
$4 - 9 = -5 \in \mathbb{Z}$

Dentro do conjunto $\mathbb{Z}$ teremos os números inteiros positivos e números inteiros negativos:

número inteiro positivo: na verdade ele constitui simplesmente um novo nome dos números naturais diferentes de zero, já conhecidos, e os símbolos +1, +2, +3, …; passam a ser os novos numerais desses mesmos números, o que nos permite escrever. $$ +1 = 1; +2 = 2; +3 = 3;$$
números opostos: os números +1 e -1, +2 e -2, +3 e -3, são chamados de números opostos, um do outro.
Valor absoluto: chama-se valor absoluto de um inteiro relativo, o próprio número se ele for positivo ou nulo, ou o seu oposto, se ele for negativo. Exemplos de valor absoluto: $+8 = 8; -8 = 8; 0 = 0.$

Observação: O valor absoluto é sempre um número natural.

Relação de ordem dos Inteiros

1. Qualquer número positivo é maior do que zero: $+2 > 0; +3 > 0$ ;
2. Zero é sempre maior que qualquer número negativo: $0 > -m.$
3. Entre dois números positivos, o maior é o que possui maior valor absoluto. Exemplo: $+7 > +3$ ;
4. Entre dois números negativos, o maior é o que tem menor valor absoluto. Exemplo: $-6 > -8; -2 > -5.$

Operações Entre Números Inteiros:

Adição:

com sinais iguais: calcula-se a soma dos valores absolutos dos números, e repete-se o sinal deles, na soma (resultado). Por exemplo, $2 + 8 = 10$ .
com sinais diferentes: determina-se a diferença entre os seus valores absolutos dando ao resultado, o sinal do maior em valor absoluto. Por exemplo: $5 + (-4) = 1.$

Observação: Quando se efetuar a adição de três ou mais números inteiros relativos, faz-se a adição das parcelas positivas, separadamente da adição das parcelas negativas, reduzem-se os resultados a um só termo, como se fossem dois inteiros relativos.

Subtração:

Adiciona-se ao minuendo (1.º), o oposto do subtraendo (2.º). Por exemplo: $(+7) + (-4) = +3$ ou $(+7) + (-4) = +3.$ .

Regra para eliminação do parênteses: Um parênteses contendo uma adição de números relativos e precedido pelo sinal “-” (negativo) pode ser eliminado, juntamente com o sinal “-“, que o precede, escrevendo-se os números nele (parênteses) contidos com seus sinais trocados. Por exemplo: $7 - (+3 - 11 + 5 - 2) = 7 - 3 + 11 - 5 + 2 = 12.$

Multiplicação:

O produto de dois números relativos de sinais iguais é um número positivo. O produto de dois números relativos de sinais diferentes, é um número negativo. Por exemplo:

$(+4) \times (+3) = +12 = 12.$
$(-8) \times (-2) = +16 = 16.$
$(-4) \times (+5) = -20.$

A Regra de Sinais para a Multiplicação:

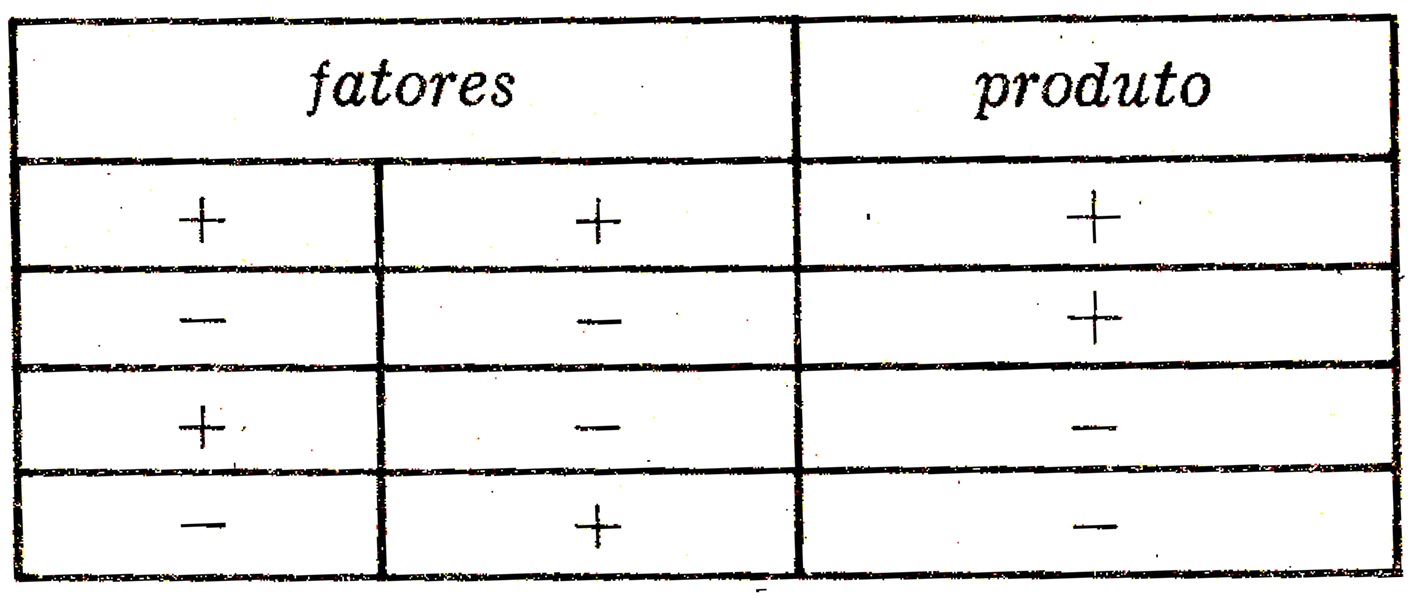
Produto de três ou mais números inteiros relativos: O produto de três ou mais números inteiros relativos é o número real que se obtém multiplicando o primeiro pelo segundo, a seguir o produto obtido pelo terceiro e assim por diante, até o último fator.

$(+) \cdot (+) \cdot (+) = +$
$(+) \cdot (+) \cdot (-) = -$
$(+) \cdot (-) \cdot (+) = -$
$(+) \cdot (-) \cdot (-) = +$

Divisão

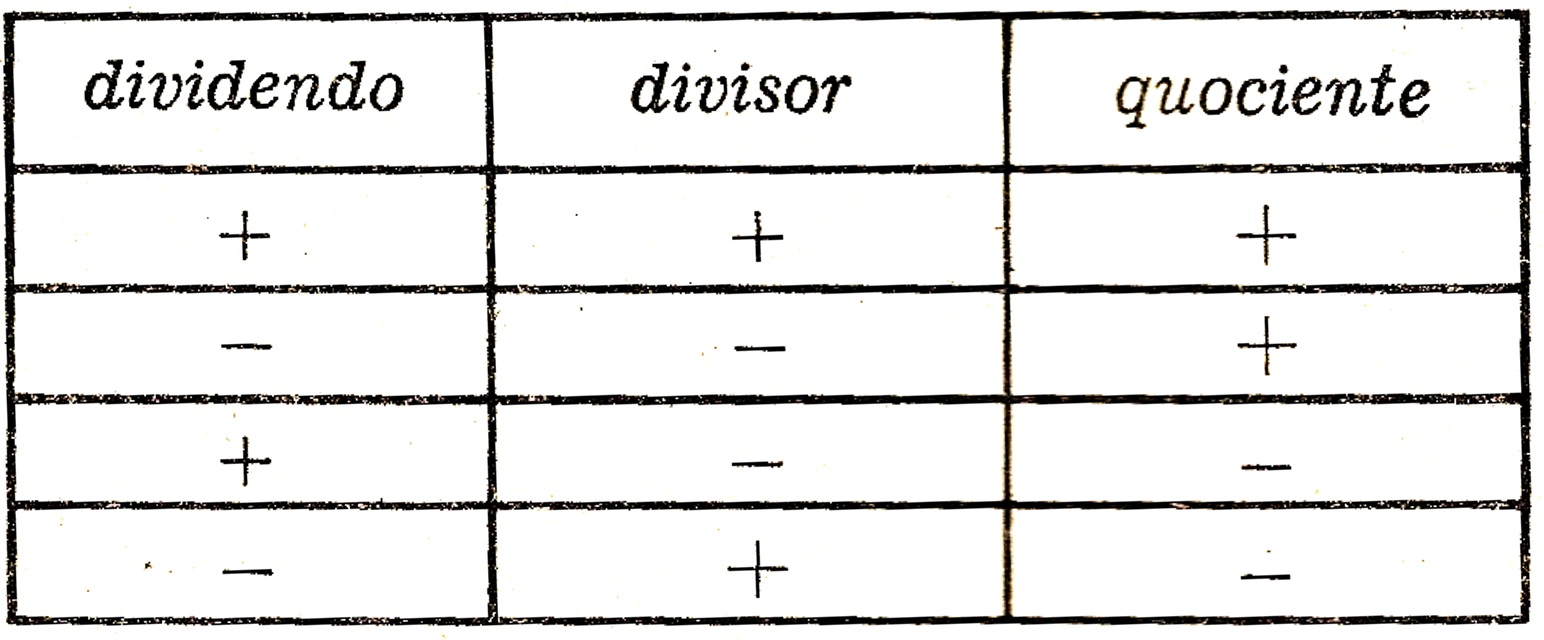
Quociente: dados dois números inteiros relativos, o segundo dos quais diferente de zero, chama-se quociente do primeiro pelo segundo, um terceiro número que, multiplicado pelo segundo (divisor), dá por produto o primeiro (dividendo). Exemplo: $(+10) : (+2) = +5.$

Potenciação

Potência de um número inteiro relativo é um produto de dois ou mais fatores iguais a esse número. Por exemplo: $(-2)^2 = (-2) \cdot (-2) = +4.$

Propriedades das Potências:

Produto de duas ou mais potências de mesma base: conserva-se a base e soma os expoentes. Exemplo: $(2)^3 \cdot (2)^2 = (+2)^{3+2} = (+2)^5$ ;
Quociente de duas potências de mesma base: conserva-se a base e subtrai os expoentes. Exemplo: $(-7)^8 \div (-7)^6 = (-7)^{8-6} = (-7)^2$ ;
Potência de uma potência: conserva-se a base e multiplica-se os expoentes. Exemplo: $((-2)^3)^5 = (-2)^{3 \cdot 5} = (-2)^{15}$ ;
Potência de um produto: Multiplica-se a potência do produto na potência de cada uma das parcelas do produto. Por exemplo: $\left[ (+3)^2 \cdot (-4)^3 \right]^5 = (+3)^{10} \cdot (-4)^{15}$ ;
Potência de um quociente: Multiplica-se a potência do produto na potência de cada uma das parcelas do quociente. $\left[ (-6)^3 \cdot (+2)^4) \right]^4= (-6)^{12} \div (+2)^{16}.$

Números Racionais Relativos

O conjunto dos números racionais relativos será reconhecido por $\mathbb{Q}$ , e será constituído por números racionais positivos, pelo zero, e pelos números racionais negativos: $$ \mathbb{Q} = \{ -2, -\frac{7}{4}, \ldots, -1,0, +1, +\frac{7}{4} \}.$$

Apoie Nosso Trabalho:

Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697

Operações

As regras operatórias e as propriedades das diversas operações com os números inteiros relativos são extensivos aos números racionais relativos.

Exemplo de adição e subtração : $\dfrac{-3}{4} + 4 - \dfrac{1}{2} = \dfrac{-3 + 32 -4}{8} = \dfrac{25}{8}$ ;
Exemplo de multiplicação e divisão: $\dfrac{-2}{3} \cdot \dfrac{5}{-4} = \dfrac{(-2) \cdot (5)}{3 \cdot (-4)} = \dfrac{-10}{-12} = \dfrac{5}{6}$ ;
Exemplo de potenciação: $\left(\frac{+2}{+5}\right)^2 = \frac{4}{25}$ .

Desiguladade

Para a desigualdade no conjunto $\mathbb{Q}$ dos números racionais relativos; adota-se as mesmas considerações feitas para a desigualdade no conjunto $\mathbb{Z}$ , isto é: — para compararmos dois números racionais relativos basta subtrairmos um do outro. Se a diferença for um número positivo, então minuendo > subtraendo; se for negativo, então minuendo < subtraendo. Se a diferença for zero os números são iguais.

Por exemplo: $$ (-5) – \left(-\frac{3}{4}\right) = -5 + \frac{3}{4} = -\frac{17}{4} $$ $$-5 < -\frac{3}{4} \;\;\; \text{ (menor)}.$$

Conclusão

Este guia ofereceu uma visão abrangente sobre números inteiros e racionais relativos, suas operações e como eles se comparam. Esperamos que agora você tenha uma compreensão clara e possa aplicar esses conceitos em suas questões matemáticas.

Álgebra Básica: Inteiros Relativos, Racionais Relativos e Relação de Ordem

Introdução