Números Naturais: Lendo, Escrevendo e Compreendendo o Valor Posicional

Se você está procurando uma explicação clara e concisa do valor posicional de números naturais, você veio ao lugar certo! Leia este artigo para saber mais.

O valor posicional é um conceito fundamental em matemática, especialmente quando se trata de números naturais. Neste artigo, explicaremos o que é valor posicional em números naturais e como ele é usado para representar números de forma clara e concisa. Se você está procurando um guia claro e fácil de entender, continue lendo!

O que São Números Naturais?

O conjunto dos números naturais é indicado por \mathbb{N} e é formado pelos elementos $$0,1,2,3,4,5,6,7,8,9,10,…$$ Este conjunto é infinito e limitado inferiormente, ou seja, ele possui um primeiro elemento que é o 0. Sendo assim, sabemos que 1 é um elemento de \mathbb{N} e indicamos tal relação por $$1 \in \mathbb{N}.$$ Por outro lado, sabemos que o elemento -10 não pertence ao conjunto \mathbb{N} e indicamos isso pela relação $$-10 \notin \mathbb{N}.$$

Em análise, o conjunto dos números naturais \mathbb{N} é caracterizado pelos chamados Aximomas de Peano:

1. Todo número natural possui um sucessor que ainda é um número natural e números naturais diferentes possuem sucessores diferentes.
2. Existe um único natural 1 que não é sucessor de nenhum outro natural.
3. PRINCÍPIO DA INDUÇÃO: Todo número natural pode ser obtido a partir de 1.

O Sistema de Numeração Decimal

O valor posicional esta amparado pelo princípio da posição decimal:

PRINCÍPIO DA POSIÇÃO DECIMAL: Todo algarismo colocado imediatamente à esquerda do outro, representa unidade de ordem, imediatmente superiores a estes (10 vezes maior) sendo que o primeiro à direita representa a unidade simples.

As características fundamentais  deste sistema de numeração decimal são:

1. Base dez na contagem;
2. Os dez algarismos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 para formar os numerais;
3. O princípio da posição decimal, para a colocação dos algarismos

Além disso, teremos as ordens, que são as unidades, dezenas, centenas, milhares, etc., também chamadas posições. Chamaremos de base de uma contagem ao número de elemento do agrupamento que se faz para contar os elementos do conjunto. Por exemplo, quando os palitos de uma caixa de fósforos são contados um a um, dize-se que foi empregada a base 1. No caso da base decimal, agruparemos em conjuntos de 10.

O que é Valor Posicional?

Em suma, o valor posicional é o valor que um dígito tem com base em sua posição em um número. Em outras palavras, o valor de um dígito depende se ele está na casa das unidades, dezenas, centenas, etc. Por exemplo, no número 345, o 5 vale 5 unidades, o 4 vale 4 dezenas e o 3 vale 3 centenas. O valor posicional é importante porque nos permite representar grandes números de forma clara e concisa.

Mas vamos explicar isso melhor!

Antes, pense e responda às questões abaixo:

1) Escrevi 14 675, troquei de lugar os algarismos  7 e 5 e obtive 14 657.

1. 1. O número que escrevi primeiro é maior ou menor que o número que obtive?
   2. Antes da troca: quanto valia 5 no primeiro númro? e o 7?
   3. Depois da troca: quanto passou a valer o 5? E o 7?

2) Agora, veja este outro número: 7 056

1. 1. Que troca eu devo fazer para o 6 aumentar seu valpr em 100 vezes? Que número eu obtenho neste caso?
   2. Que troca eu devo fazer para o 6 aumentar seu valor em 10 vezes? Que número eu obtenho neste caso?

Você observou que o valor do algarismo depende da posição que ele ocupa no número?

• No número 26, o valor do algarismo 2 é 2 \times 10 , ou seja, 20 unidades, porque ele ocupa a posição ou a ordem das dezenas.
• No número 263, o valor do algrismo 2 é 2 \times 100 , ou seja, 200 unidades, porque ele ocupa a posição ou a ordem das centenas.

Vamos considerar o número 8 594:

Escrevemos o número 8 594 por extenso e o lemos assim: oito mil, quinhentos e noventa e quatro.

Veja o quadro de ordens até a décima ordem:

Vamos, agora, considerar o número natural 97 025, localizá-lo no quadro de ordens e escrever como se lê esse número.

Lendo e Escrevendo um Número Natural

No sistema de numeração decimal, os número dão lidos ou escritos mais facilmente que separamos os algarismos em grupos de três, começando pela direita. Isso porque cada três ordens forma uma classe. Veja os números

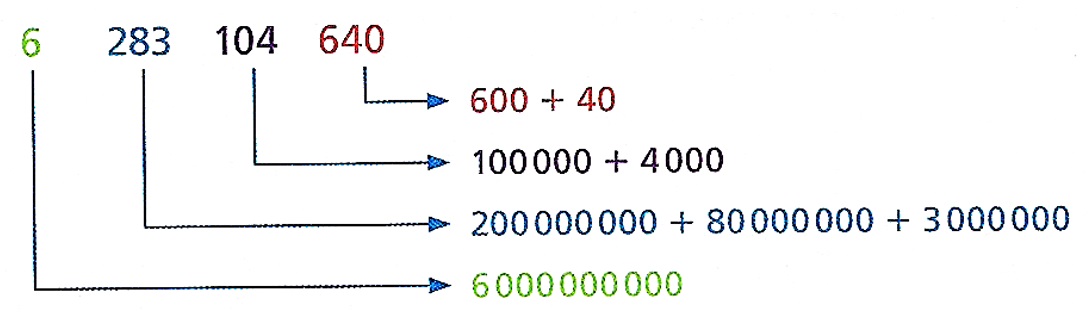
6 283 104 640                                       5 000 254

Cada grupo de três algarismo constitui uma classe, e cada classe tem um nome, como podemos ver no quadro abaixo:

O quadro de ordens no ajuda a ler, escrever, compor e decompor números. Assim:

Lemos ou escrevemos por extenso: seis bilhões, duzentos e oitenta e três milhões, cento e quatro mil, seiscentos e quarenta

Quando todas as ordens de uma classe são representadas por zero, não se lê esssa classe. Lemos ou escrevemos por extendo: cinco milhões, duzentos e cinquenta e quatro.

Agora, veja este número escrito por extenso: sessenta mil, trezentos e vinte e oito. No quadro de ordens, podemos representar esse número usando algarismos assim:

Temos o  número 60 328.

Observações Finais

1. Devemos ainda observar o que é o valor absoluto d eum algarismo: é o valor que ele representa quando considerado isoladamente como podemos ver no exemplo abaixo:
2. Os números podem ser representados utilizando-se outras bases que não a base decimal; tais bases formarão novos sistemas numéricos onde seus elementos diferenciarão daqueles constituintes do sistema decimal. Tomando-se um número de determinado sistema como referencial, pode-se realizar mudança de base determinando o numeral que le será correspondente na nova base;
3. O símbolo “zero” serve para indicar as ordens vazias. Enquanto os algarismos de um a nove são chamados de “algarismos significativos”, “zero” é chamado de “algarismo insignificativos”.

Referências Bibliográficas:

1. JUNIOR, G., RUY, J. A conquista da matemática, 6º ano. FTD. (2018, p. 15). PNLD 0377P2002 – Link do livro.
2. B. BOYER, Carl. História da Matemática. São Paulo: Bluncher, 2012. – Link do livro.
3. LERER, ISAAC. Novíssimo Manual do Estudante Ilustrado – Ensino Integrado e Supletivo: Matemática e Informática.

Leia Mais Sobre Matemática do Ensino Fundamental:

• Sistemas de Numeração: Números Egípcios, Babilônicos e Romanos.
• O Sistema de Numeração Decimal Indo-Arábico.
• As 7 Maneiras Pelas Quais a Matemática Pode Salvar o Mundo Segundo os Cientistas.
• A beleza da matemática na Razão Áurea (ou Número de Ouro)
• 5 cientistas brasileiros que poderiam ter ganhado o Prêmio Nobel