A Matriz Jacobiana é usada para realizar mudanças de variáveis, em especial para transformar os vetores infinitesimais de um sistema de coordenadas para outro. Neste artigo queremos estudar um pouco mais este objeto matemático.

Introdução
Olá, seja bem-vindo(a)! Neste artigo, quero compartilhar minha experiência no estudo do Jacobiano, abordando tanto a Matriz Jacobiana quanto o Determinante Jacobiano de forma clara e direta.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Sei que muitas pessoas pesquisam esses termos no Google para entender melhor como funcionam em Cálculo Diferencial e Integral. Por isso, meu objetivo aqui é explicar de maneira simples o que é a matriz, como calcular o determinante e, acima de tudo, mostrar onde isso pode ser aplicado em situações práticas.
Primeiramente, é importante saber que a Matriz Jacobiana (denominada por causa do matemático alemão Carl Gustav Jakob Jacobi) é a matriz formada pelas derivadas parciais de primeira ordem de uma função vetorial.
Se uma função é diferenciável num ponto, a sua derivada é dada em coordenadas pela matriz Jacobiana, mas uma função não precisa de ser diferenciável para a existência desta matriz, basta que as derivadas parciais existam.
O que é a Matriz Jacobiana?
Ao estudar funções de várias variáveis, sempre faço uma pausa para entender como cada variável está inter-relacionada. A Matriz Jacobiana me ajuda justamente a ter uma visão panorâmica de todas as derivadas parciais que compõem a função.
Cada linha e coluna carrega informações cruciais sobre como a função se comporta quando alteramos uma variável específica, o que é fundamental para aplicações em mudança de variáveis e até em otimização.
Como Calcular a Matriz Jacobiana em duas e três dimensões?
Por exemplo, no caso de uma função f(u,v) = \left( x(u,v) , y(u,v) \right) a matriz jacobiana de x e y em relação a u e v é dada por $$ \frac{\partial (x,y)}{\partial (u,v)} = \left[ \begin{array}{ll} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array} \right]. $$
De modo análogo, a matriz jacobiana de x,y e z em relação a u, v e w é dada por $$ \frac{\partial (x,y,z)}{\partial (u,v,w)} = \left[ \begin{array}{ccc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\ \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w}\\\end{array} \right].$$
A Matriz Jacobiana em Coordenadas Polares
As equações $$x=r\text{cos} ( \theta )\;\;\;\;y=r\text{sen} ( \theta )$$ que nos dão as coordenadas cartesianas de um dado ponto em termos de suas coordenadas polares.
A matriz jacobiana, nesse caso, é dada por $$ \frac{\partial (x,y)}{\partial (u,v)} = \left[ \begin{array}{ll} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right] = \left[ \begin{array}{ll} \text{cos} ( \theta ) & -r\text{sen} ( \theta )\\ \\ \text{sen} ( \theta ) & r\cos{ \theta} \end{array} \right] .$$
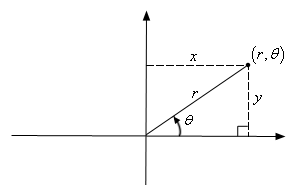 Equivalência entre os sistemas de coordenadas cartesianas e polares.
Equivalência entre os sistemas de coordenadas cartesianas e polares.
A Matriz Jacobiana em Coordenadas Cilíndricas
As coordenadas cilíndricas de um ponto P, cujas coordenadas cartesianas são (x,y,z), no espaço são dadas por $$r, \theta, z$$ onde r e \theta são as coordenadas polares da projeção de P sobre o plano xy .
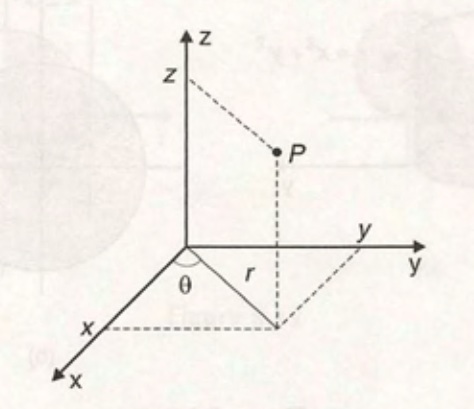 Coordenadas Cilíndricas
Coordenadas Cilíndricas
Desta forma, como $$x(r, \theta, z) = r \text{cos} ( \theta ),$$ $$y(r, \theta, z) = r \text{sen} ( \theta )$$ e z(r, \theta, z)=z a matriz jacobiana de x,y e z em relação a r, \theta e z é dada por $$\left[ \frac{\partial (x,y,z)}{\partial (u,v,w)} \right] = \left[ \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z}\\ \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}\\\end{array} \right] = \left[ \begin{array}{ccc}
\text{cos} ( \theta ) & – r \text{sen} ( \theta ) & 0\\ \\ \text{sen} ( \theta ) & r \text{cos} ( \theta ) & 0\\ \\ 0 & 0 & 1\\\end{array} \right] .$$
A Matriz Jacobiana em Coordenadas Esféricas
As coordenadas esféricas de um ponto P, cujas coordenadas cartesianas são (x,y,z), no espaço são dadas por $$r, \theta, \phi$$ onde r é a distância de P até a origem, \theta é mesma das coordenas cilíndricas e \phi é o ângulo formado pelo eixo positivo dos z e o segmento que une o ponto P à origem.
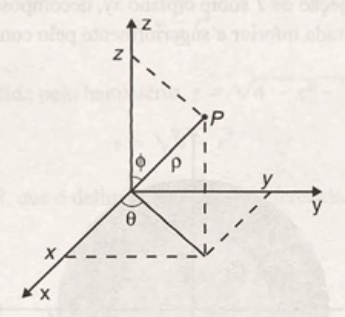 Coordenadas Esféricas
Coordenadas Esféricas
Desta forma, $$x(r, \theta, \phi) = r \text{cos} ( \theta )\text{sen} ( \phi ),$$ $$y(r, \theta, \phi) = r \text{sen} ( \theta )\text{sen} ( \phi )$$ e z(r, \theta, \phi)=r \text{cos} ( \phi ) e a matriz jacobiana de x,y e z em relação a r, \theta e \phi é dada por $$\left[ \frac{\partial (x,y,z)}{\partial (r, \theta , \phi)} \right] = \left[ \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \phi}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \phi}\\ \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \phi}\\\end{array} \right] = \left[ \begin{array}{ccc} \text{cos} ( \theta )\text{sen} ( \phi ) & -r \text{sen} ( \theta ) \text{sen} ( \phi ) & r \text{cos} ( \theta ) \text{cos} ( \phi )\\ \\ \text{sen} ( \theta )\text{sen} ( \phi ) & r \text{cos} ( \theta ) \text{sen} ( \phi ) & r \text{sen} ( \theta ) \text{cos} ( \phi )\\ \\ \text{cos} ( \phi ) & 0 & -r\text{sen} ( \phi )\\\end{array} \right] .$$
A definição geral da Matriz Jacobiana
Seja f: \mathbb{R}^m \rightarrow \mathbb{R}^n , definida num conjunto aberto U \subset \mathbb{R}^m por $$f = (f_1 , f_2 , f_3 , … , f_n )$$ onde $$f_i : \mathbb{R}^m \rightarrow \mathbb{R}$$, é diferenciável no ponto a \in U , sua derivada é a aplicação linear f'(a) : \mathbb{R}^m \rightarrow \mathbb{R}^n , caracterizada por $$ f(a+v) – f(a) = f'(a)\cdot v + r(v), \qquad \text{com } \lim_{v \rightarrow 0}{\frac{r(v)}{|v|} } = 0.$$
A transformação linear f'(a) : \mathbb{R}^m \rightarrow \mathbb{R}^n possui, em relação às bases canônicas de \mathbb{R}^m e \mathbb{R}^n , uma matriz n \times m chamada matriz jacobiana de f no ponto a , dada por $$ Jf(a) = \left[ \begin{array}{lll} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_m} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_m} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots & \frac{\partial f_n}{\partial x_m} \\\end{array} \right]$$ onde a k-ésima linha da matriz é dada pela transposta do gradiente de f_k : \mathbb{R}^m \rightarrow \mathbb{R} .
A Matriz Jacobiana pode ser uma matriz não quadrada?
Como consequência direta desta definição podemos perceber que a matriz Jacobiana pode ser de qualquer forma. Pode ser uma matriz retangular, onde o número de linhas e colunas não é o mesmo, ou pode ser uma matriz quadrada, onde o número de linhas e colunas é igual
O Determinante Jacobiano
A matriz Jacobiana é diversas vezes referenciada como Jacobiano, mesmo este último sendo definido como o determinante da matriz Jacobiana. Ele é de grande importância na mudança de variáveis em integrais múltiplas e no Teorema da Função Inversa.
Cálculo prático do Determinante Jacobiano
Para ilustrar, gosto de mostrar passo a passo como calcular o determinante, partindo da Matriz Jacobiana. Primeiro, identifico cada derivada parcial e monto a matriz. Em seguida, aplico as regras de determinante que já conhecemos da álgebra linear. Com isso, é possível interpretar como a função de várias variáveis “distorce” a região no plano ou no espaço.
- Identifique as derivadas parciais das funções envolvidas.
- Monte a matriz, organizando cada derivada na linha/coluna correta.
- Calcule o determinante aplicando a fórmula apropriada (expansão por cofatores, diagonalização etc., dependendo do nível de detalhes que prefiro).
Exemplos de Cálculo de Jacobianos Clássicos
EXEMPLO 1 (O Determinante Jacobiano para coordenadas polares): O determinante jacobiano, nesse caso, é dado por $$\left| \frac{\partial (x,y)}{\partial (r, \theta )} \right| = \left| \begin{array}{ll} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right| = \left| \begin{array}{ll} \cos{\theta} & -r\sin{\theta}\\ \\ \sin{\theta} & r\cos{ \theta} \end{array} \right| = r.$$
EXEMPLO 2 (O Determinante Jacobiano para coordenadas cilíndricas): O determinate jacobiano, nesse caso, é dado por $$\left| \frac{\partial (x,y,z)}{\partial (r, \theta , z)} \right| = \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z}\\ \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}\\\end{array} \right| = \left| \begin{array}{ccc} \cos{\theta} & – r \sin{\theta} & 0\\ \\ \sin{\theta} & r \cos{\theta} & 0\\ \\ 0 & 0 & 1\\\end{array} \right| = r.$$
EXEMPLO 3 (O Determinante Jacobiano para coordenadas esféricas): O determinate jacobiano neste caso é dado por $$\left| \frac{\partial (x,y,z)}{\partial (r, \theta , \phi)} \right| = \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \phi}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \phi}\\ \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \phi}\\\end{array} \right| = \left| \begin{array}{ccc} \cos{\theta}\sin{\phi} & -r \sin{\theta} \sin{\phi} & r \cos{\theta} \cos{\phi}\\ \\ \sin{\theta}\sin{\phi} & r \cos{\theta} \text{sen}{\phi} & r \text{sen}{\theta} \cos{\phi}\\ \\ \cos{\phi} & 0 & -r\sin{\phi}\\\end{array} \right| = r^2\sin{\phi}.$$
EXEMPLO 4: Considere u=x-y e v=x+y. Desta forma, $$x=\frac{u}{2}+\frac{v}{2}\;\;\;e\;\;\;y=\frac{u}{2}-\frac{v}{2},$$ assim $$\left| \frac{\partial (x,y)}{\partial (u,v)} \right| = \left| \begin{array}{cc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta}\\ \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array}
\right| = \left| \begin{array}{ll} \frac{1}{2} & \frac{1}{2}\\ \\ -\frac{1}{2} & \frac{1}{2} \end{array}
\right| = \frac{1}{2}.$$
Por que o Determinante Jacobiano é importante?
Quando estou analisando uma transformação de coordenadas ou preciso fazer mudanças de variáveis em integrais múltiplas, sempre verifico o Determinante Jacobiano. Ele indica o fator de escala que a transformação exerce sobre áreas, volumes ou hipervolumes – algo essencial em Cálculo Avançado.
O Jacobiano e as Integrais Duplas
Por exemplo, para integrais duplas, por meio das mudanças de variáveis $$x = x(u,v)\;\;\;e\;\;\;y=y(u,v),$$ uma integral dupla sobre uma região R do plano xy pode ser transformada em uma integral dupla sobre uma região R' do plano uv.
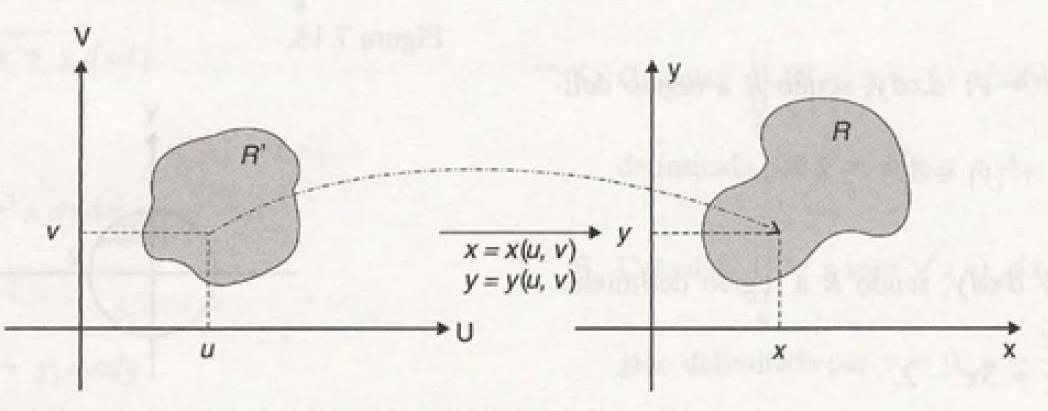 Mudança de Variável na Integral Dupla
Mudança de Variável na Integral Dupla
Desta forma, temos que
$$\int \int_{R}{f(x,y)}dxdy = \int \int_{R’}{f(x(u,v),y(u,v)}\left| \frac{\partial (x,y)}{\partial (u,v)} \right| dudv$$ onde \left| \frac{\partial (x,y)}{\partial (u,v)} \right| é o determinante jacobiano de x e y em relação a u e v, dado por $$\left| \frac{\partial (x,y)}{\partial (u,v)} \right| = \left| \begin{array}{ll}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\
\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}
\end{array}
\right|$$ desta forma, em se usarmos uma mudança de variável de coordenadas cartesianas para polares, encontramos $$\int \int_{R}{f(x,y)}dxdy = \int \int_{R’}{f(r\cos{\theta}, r\sin{\theta})r}drd\theta.$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
O Jacobiano e as Integrais Triplas
Já para integrais triplas, por exemplo, temos duas mundanças de variáveis muito importantes usando coordenadas cilíndricas e esféricas.
- Usando o jacobiano em coordenadas cilíndricas, a integração tripla é dada por $$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T’} \int{f(r \cos{\theta}, r \sin{\theta}, z)r drd\theta dz}$$ onde T' é a região T descrita em coordenadas cilíndricas.
EXEMPLO: Calcule $$I = \int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz},$$ onde T é o cilindro x^2+y^2 \leq 1, 0\leq z\leq 1. Em coordenads cilindricas, $$x=r \cos{\theta}, y=r\sin{\theta}, z=z$$ e, daí $$ \int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz} = \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi} \int\limits_{0}^{ 1}{\sqrt{r^2+ z^2}rdrd\theta dz} . $$ Para ver a solução desta integral tripla basta estudar este nosso artigo.
- Usando jacobiano em coordenadas esféricas, a integração tripla é dada por $$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T’} \int{f(r \cos{\theta}\sin{\phi}, r \sin{\theta}\sin{\phi}, r\cos{\phi})r^2\sin{\phi} drd\theta d\phi }$$ onde T' é a região T descrita em coordenadas esféricas.
EXEMPLO: Calcule a $$\int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz}$$ sendo T a esfera de raio 1 e centro na origem do \mathbb{R}^3 . Utilizando-se de coordenadas esféricas obtemos $$x(r, \theta, \rho) = r \cos{\theta}\sin{\phi},$$ $$y(r, \theta, \rho) = r \sin{\theta}\sin{\phi},$$ $$ \int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz} = $$ $$= \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi} \int\limits_{0}^{\pi}{\sqrt{(r \cos{\theta}\sin{\phi})^2+ (r \sin{\theta}\sin{\phi})^2 + (r \cos{\phi})^2}r^2\sin{\phi}drd\theta d\phi} = $$ $$ = \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi} \int\limits_{0}^{\pi}{r^3\sin{\phi}}drd\theta d\phi $$ Para ver a solução completa desta integral tripla basta estudar este nosso artigo.
Qual a aplicação do Jacobiano na Engenharia?
O Jacobiano pode ser usado para determinar a estabilidade de equilíbrios para sistemas de equações diferenciais aproximando o comportamento na vizinhança de um ponto de equilíbrio. Suas aplicações incluem determinar a estabilidade do equilíbrio livre de doença na modelagem de doenças.
Além disso, a Jacobiana representa a melhor aproximação linear de uma função diferenciável nas vizinhanças de um ponto. Essa aproximação é de grande importância no cálculo numérico, onde a matriz Jacobiana e seu determinante são utilizados para resolver sistemas não-lineares pelo método de Newton (ou método do Gradiente Iterativo).
Por fim, podemos afirmar que as Matrizes Jacobianas são uma ferramenta muito utilizada em toda a robótica e teoria de controle. Basicamente, um Jacobiano define a relação dinâmica entre duas representações diferentes de um sistema.
Conclusão:
Chegamos ao fim desta exploração sobre Jacobiano, Matriz Jacobiana e Determinante Jacobiano. Espero ter contribuído para um melhor entendimento desses conceitos tão relevantes no Cálculo Diferencial e Integral. Tenho notado o quanto essas ferramentas são fundamentais para problemas que envolvem transformação de variáveis e cálculos de integrais em dimensões superiores.
Se você tem alguma dúvida ou quer compartilhar uma experiência relacionada, deixe um comentário aqui no artigo. Quero muito saber como você está aplicando a Matriz Jacobiana ou o Determinante Jacobiano nos seus estudos ou pesquisas. E, se achou este conteúdo útil, compartilhe-o com outras pessoas que também possam se beneficiar desses conceitos.
Por fim, se você quer se aprofundar ainda mais no universo do Cálculo, desenvolvendo um entendimento sólido sobre derivadas, transformações e todas as aplicações práticas, convido você a conhecer o meu curso neste link. Lá, o professor Lucas Stolerman, doutor em matemática pelo IMPA e atualmente professor na Oklahoma State University, com 15 anos de experiência no ensino da matemática, vai te guiar no caminho da aprovação em Cálculo.
Obrigado pela leitura e continue acompanhando o blog para ver mais conteúdos sobre matemática e aplicações práticas!
Leia Mais:
- A Diferenciabilidade de Funções de Várias Variáveis a Valores Reais
- Coordenadas Polares e a Mudança de Variável nas Integrais Duplas
- Funções Dadas Implicitamente e o Teorema das Funções Implícitas
- Mudança de Variável em Integrais Triplas | Coordenadas Cilíndricas e Esféricas
Referências Bibliográficas do Artigo:
- Wilfred Kaplan – “Advanced Calculus” [Link do livro]
- Erwin Kreyszig – “Matemática Superior para Engenharia – Vol. 1 e 2” [Link do livro 1] [Link do livro 2]
- Hamilton Luiz Guidorizzi – “Um Curso de Cálculo, vol. 3” [Link do Livro]
- Elon Lages Lima – “Curso de Análise, vol 2” [Link do Livro]



