A Teoria dos Jogos é um ramo da Matemática Aplicada que estuda situações em que duas ou mais partes se confrontam, no sentido de maximizarem seus ganhos.
Em geral, a Teoria de Jogos pode ser usada quer para prever o resultado de uma situação de confronto, quer para aconselhar um dos confrontantes a tomar a melhor decisão.
É claro que as situações consideradas são em geral demasiado complexas para que as simples considerações matemáticas deem a solução final.
Vamos considerar alguns jogos clássicos que envolvem matemática e podem ser adaptados para a sala de aula e ajudar como ferramentas de ensino-aprendizagem.
O JOGO DO SIM
Dados os vértices de um hexágono regular, dois jogadores (laranja e azul) alternam unindo dois vértices com um segmento da sua cor.
Quem completar um triângulo monocromático perde.
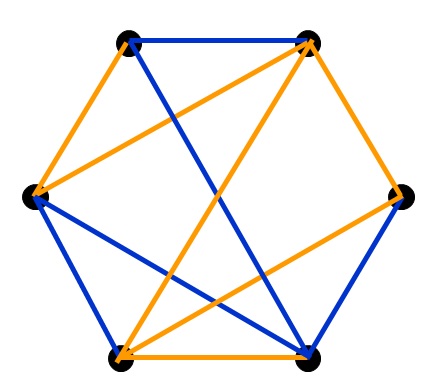 Nessa simulação de um jogo do SIM, o jogador representado pela cor laranja perdeu.
Nessa simulação de um jogo do SIM, o jogador representado pela cor laranja perdeu.
O jogo do SIM seria bastante desinteressante se o empate fosse possível. Mas acontece que não é.
No jogo do SIM sempre há um vencedor e um perdedor e isso pode ser demonstrado matematicamente usando o Princípio das Gavetas de Dirichlet.
O JOGO DAS PEDRAS
Têm-se uma quantidade arbitrária de pedras dispostas em vértices de um polígono regular.
Dois jogadores se alternam retirando estas pedras.
Cada jogador pode retirar somente uma pedra, ou então pode retirar duas, desde que sejam vizinhas ( isto é, localizadas em vértices consecutivos do polígono ).
Ganha aquele que retirar a última pedra.
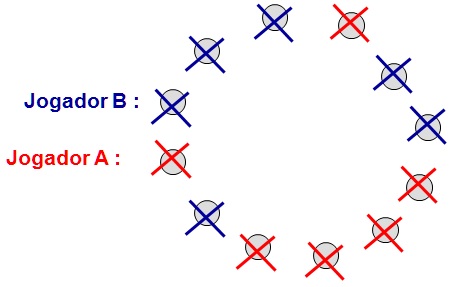 Nesse exemplo do Jogo das Pedras o jogador B venceu
Nesse exemplo do Jogo das Pedras o jogador B venceu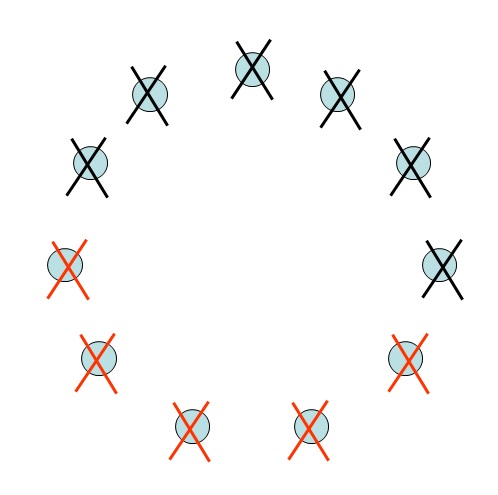 Nesse exemplo do Jogo das Pedras, temos uma quantidade ímpar de pedras e o preto venceu, pois retirou a última pedra.
Nesse exemplo do Jogo das Pedras, temos uma quantidade ímpar de pedras e o preto venceu, pois retirou a última pedra.
Jogo do NIM
Dois jogadores alternam escolhendo uma pilha de feijões e tirando feijões ( podem ser todos) desta pilha. Ganha quem retirar o último feijão.
Acredite, o jogo é mais complexo do parece e desenha estratégias interessantes dentro da teoria dos jogos.
o nascimento da teoria dos jogos combinatórios.
O nome NIM é derivado da palavra alemã nimm, cuja tradução é retirada. É um jogo tático, provavelmente inspirado no antigo jogo de apostas chinês Fan Tan.
HEX
Dois jogadores alternam colocando peças da sua cor num hexágono livre, tentando unir duas margens paralelas.
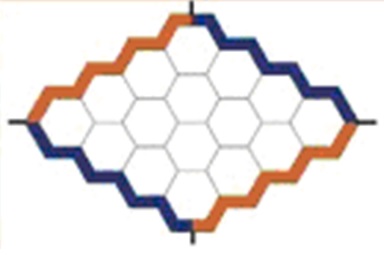
Neste jogo, inventado por Piet Hein e reinventado por John Nash, não há empates.
Uma maneira intuitiva de ver isto é pensar na cor laranja como tijolo e no azul como água de um rio.
Ao encher todos os hexágonos do tabuleiro, ou a água corre, e os azuis ganham, ou não corre, e ganham os de cor laranja uma vez que estes tijolos barraram a água.
O matemático David Gale provou que o fato de o Hex não ter empates permite provar o teorema do Ponto Fixo de Brower.
Reciprocamente, se assumirmos que o Teorema do Ponto Fixo de Brower é verdadeiro, conseguimos provar que no jogo Hex nunca ocorre empate.
Trata-se, portanto, de proposições equivalentes.
A prova desta afirmação foge dos nossos objetivos, mas este comentário serve para ilustrar que um jogo inocente tem forte relação com um Teorema matemático que, por sua vez, tem importantes aplicações práticas.
TANGRAM
O quebra-cabeça Tangram pode ter até mais de 4000 anos de idade, dependendo de qual fonte você consultar.
Na China este quebra-cabeças era designado por Chi Pae Pan, que se pode traduzir por O Jogo das Peças da Sabedoria, ou ainda O Jogo das Sete Peças da Astúcia, e cada peça chama-se um tan.
 Tangram
Tangram
O desafio do quebra-cabeças é recompor estas formas mudando as sete peças de posição, sendo que ele funciona como um excelente artifício de ensino da geometria.
Pode-se pedir que usando as peças do Tangram se construa figuras geométricas usando um número limitado de peças e até mesmo com todas as peças.
O Tangram tem, por um lado, uma componente lúdica, mas pode ser estudado de um ponto de vista matemático. Umas das perguntas que se pode fazer é: qual é a relação entre as áreas das várias peças?
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Faça, por exemplo, o seguinte exercício:
Calcule a área de cada peça do Tangram e verifique que as áreas vão duplicando das peças menores para as maiores.
Há muitas figuras de grande elegância que podem ser construídas com o Tangram.
Abaixo vemos algumas delas:
 Exemplos de figuras possíveis de se construir com o Tangram
Exemplos de figuras possíveis de se construir com o Tangram
A TORRE DE HANÓI
A Torre de Hanói é um dos quebra-cabeças matemáticos mais populares. Ele foi inventado por Edouard Lucas em 1883.
As peças são n discos de tamanhos diferentes e todos com um furo em seu centro e três pinos onde são colocados os discos. Certamente podem ser encontrados em qualquer loja de brinquedos.
Inicialmente os discos formam uma torre onde todos são colocados em um dos pinos em ordem decrescente de tamanho.
Devemos transferir toda a torre para um dos outros pinos de modo que cada movimento é feito somente com um disco, nunca havendo um disco maior sobre um disco menor.
Queremos saber qual é o menor número de movimentos necessários para resolver uma torre de Hanói com n discos.
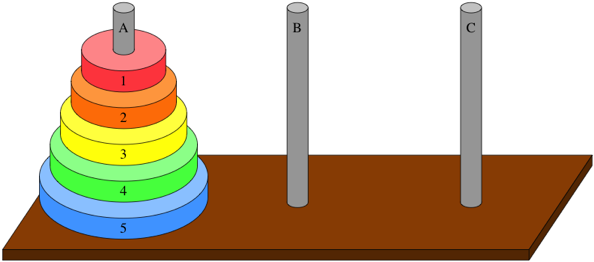 Torre de Hanoi com 5 Discos
Torre de Hanoi com 5 Discos

