Integral de Superfícies | 1ª Lista de Execícios Resolvidos

A integral de superfície de f(x,y,z) sobre a superfície \mathbb{S} é dada por $$\int\limits_{\mathbb{S}}\int{f(x,y,z) dS}.$$ Por outro lado, seja \vec{F} um campo vetorial definido sobre \mathbb{S}, a Integral de Superfície de \vec{F} sobre \mathbb{S} é denotada por $$\int\limits_{\mathbb{S}}\int{\vec{F} . \vec{n} dS} = \int\limits_{R}\int{\vec{F}(x(u,v), y(u,v), z(u,v)) . \vec{n} (u,v) \left\| \frac{\partial r}{\partial u} \wedge \frac{\partial r}{\partial v} \right\| dudv} .$$

Leia Mais: Artigo completo e detalhado sobre Integral de Superfície

Integral de Superfície: 1ª Lista de Exercícios Resolvidos:

1. Calcule $$\int\limits_{\mathbb{S}}\int{\frac{\sigma}{\sqrt{x^2+y^2+(z+1)^2}} dS},$$ no hemisfério \mathbb{S}: x^2+y^2+ z^2 = 1; z\geq 0. Esta integral de superfície está intimamente ligada ao conceito de potencial eletrostático.

SOLUÇÃO: $$\int\limits_{\mathbb{S}}\int{\frac{\sigma}{\sqrt{x^2+y^2+(z+1)^2}} dS} = \int\limits_{\mathbb{R}}\int{\frac{\sigma}{\sqrt{2 (sen(v)+1)}}cos(v) dudv} =$$ $$= \frac{ \sigma}{\sqrt{2}}\int\limits_{-\pi /2}^{\pi /2}\int\limits_{0}^{2 \pi }{\frac{cos(v)}{\sqrt{sen(v) +1}} dudv}= \pi \sigma \sqrt{2} \int\limits_{-\pi /2}^{\pi /2}{\frac{cos(v)}{\sqrt{sen(v) +1}} dudv} = 4 \pi \sigma.$$

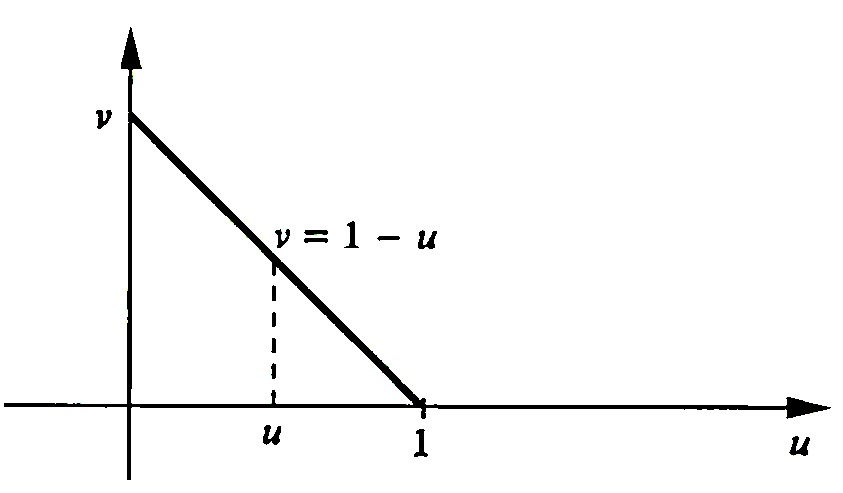
2. Calcule a área da superfície S dada por $$S: r(u,v) = (u,v,1-u^2); \qquad u \geq 0, v \geq 0, u +v \leq 1 .$$

SOLUÇÃO: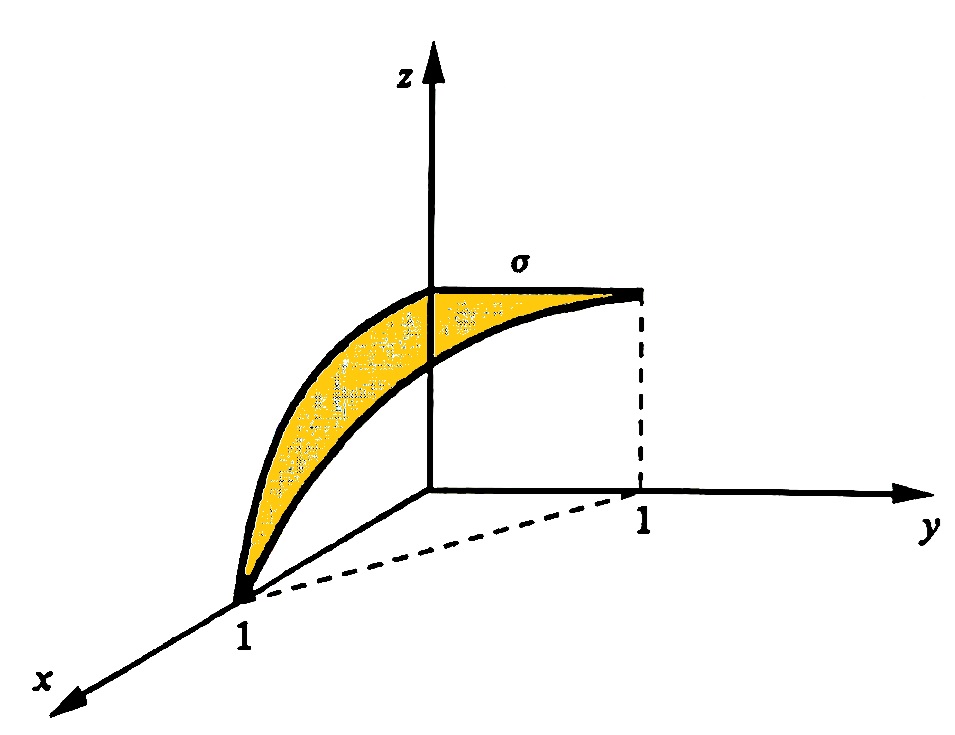 

3. Calcule a integral de f(x,y,z) = x^2 + y^2 + z^2 sobre o hemisfério z = \sqrt{R^2 - x^2 -y^2}

SOLUÇÃO: 

4. Use as integrais de superfície para calcular a área da esfera de raio a.

SOLUÇÃO: 

Leia Mais:

• Integral de Superfície | Teoremas de Stokes e da Divergência
• Integral de Superfície | Campos Escalares, Campos Vetoriais e Fluxos
• Introdução às Superfícies: Parametrização, Suavidade e Cálculo de Área.
• Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano

Assista Nossa Vídeo-Aula Sobre Integrais de Superfície