Integral de Linha de Campos Vetoriais | 1ª Lista de Exercícios Resolvidos

As Integrais de Linha e de superfície são outras formas importantes de se estender a noção de integral. Em geral, integrais deste tipo aparecem quando consideramos distribuições lineares de massa ou carga elétrica e o trabalho de uma força, por exemplo.

Vamos considerar agora L=L(x,y,z), M=M(x,y,z) e N=N(x,y,z) funções definidas e contínuas numa região R de espaço de modo que $$\vec{F}(x,y,z) = L(x,y,z)i+M(x,y,z)j+N(x,y,z)k$$ seja um campo vetorial definido no aberto R e seja C um arco regular, todo contido em R com representação paramétrica $$P(t) = x(t) i + y(t) j +z(t) k\;\;\;\;a\leq t \leq b$$ que descreve um movimento em R.

Vamos definir a integral de linha de \vec{F}, ao longo do arco C, como sendo $$\int\limits_{C}{Ldx+Mdy+Ndz} = \int\limits_{C}{\vec{F}(P(t)).dP} $$ onde F(P) = (L(P(t)),M(P(t)), N(P(t))) e dP = (x'(t)dt, y'(t)dt, z'(t)dt) = P'(t)dt.

Esta integral é denominada de integral de linha de segunda espécie e sua forma clássica é dada por $$\int\limits_{a}^{b}{[Lx’+My’+Nz’]dt}$$

Integral de Linha de 2ª Espécie | 1ª Lista de Exercícios Resolvidos

1) Calcule $$\int\limits_{C}{4xydx + (2x^2 – 3xy)dy}$$ onde a curva C consiste no segmento de reta de (-3,2) a (1,0) unida ao arco do primeiro quadrante referente à circunferência x^2 + y^1 =1 , de (1,0) a (0,1), percorrida no sentido anti-horário.

SOLUÇÃO: A figura abaixo mostra a curva C composta pelos arcos C_1 e C_2 . O arco C_1 é o segmento de reta.

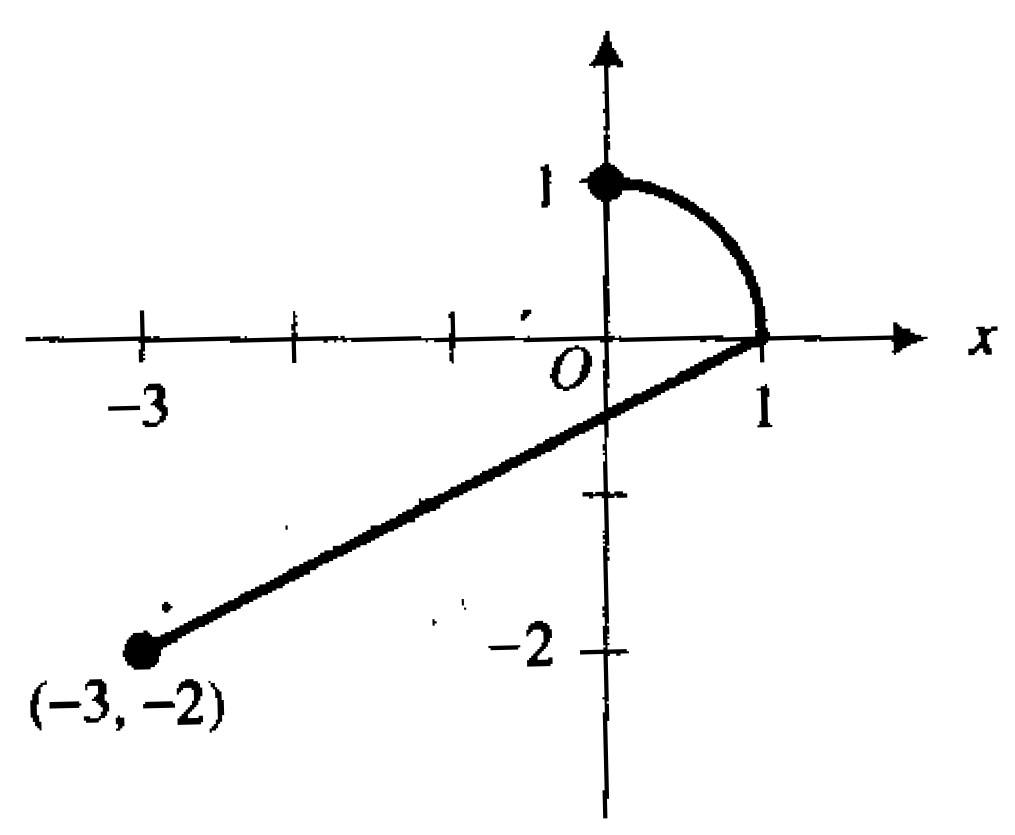
Uma equação da reta que passa pelos pontos (-3,-2) e (1,0) e x -2y = 1. Portanto, C_1 pode ser parametrizada por $$ x = 1 +2t, \qquad y = t; \qquad -2 \leq t \leq 0 .$$

O arco C_2 , que é o arco do primeiro quadrante da circunferência x^2 + y^2 = 1 , pode ser parametrizada por $$ x = cos(t), \qquad y = sen(t); \qquad 0 \leq t \leq \frac{\pi}{2}.$$

Assim, $$\int\limits_{C_1}{4xydx + (2x^2 – 3xy)dy} = \int\limits_{-2}^{0}{(18t^2+13t +2)dt }= 26$$ $$\int\limits_{C_2}{4xydx + (2x^2 – 3xy)dy} = \int\limits_{0}^{\frac{\pi}{2}}{(2 cos(t)-6cos(t)sen^2(t) – 3cos^2(t)sen(t))dt} = -1$$

Portanto, $$\int\limits_{C}{4xydx + (2x^2 – 3xy)dy} = \int\limits_{C_1}{4xydx + (2x^2 – 3xy)dy} + \int\limits_{C_2}{4xydx + (2x^2 – 3xy)dy} = 26-1 = 25.$$

2) Calcule $$\int_{C}{\sqrt{3}{x}}dx+\frac{dy}{1+y^2}$$ onde C é a curva representada na figura abaixo.

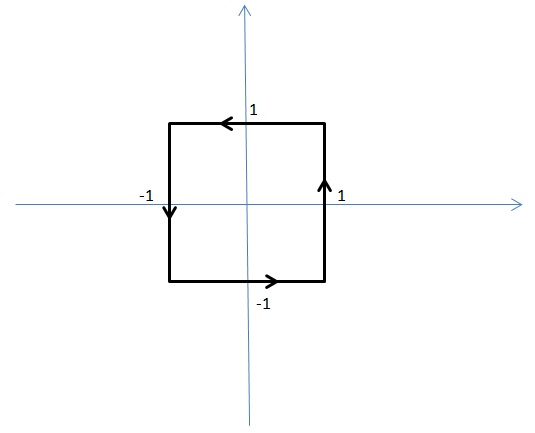
SOLUÇÃO: 

3) Integrar a forma $$yxdx – xzdy + xyzdz $$ao longo da poligonal P_1 P_2 P_3 P_4 onde $$ P_1 (1,1,1); P_2 (2,1,1); P_3 (2,2,1);  P_4 (2,2,2) .$$

SOLUÇÃO: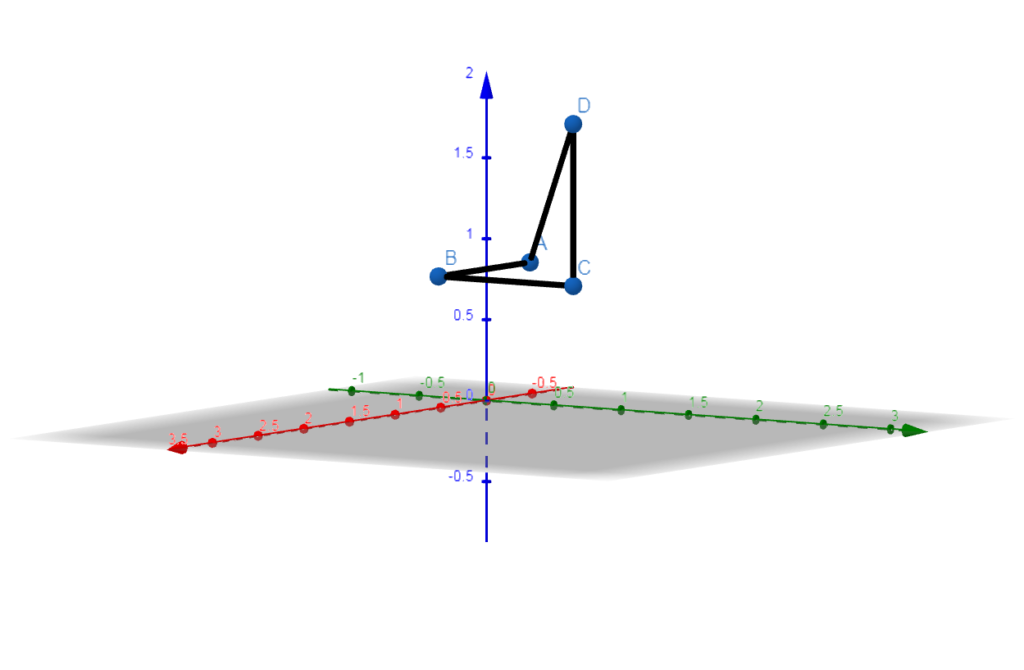 

4) Considere a função \vec{F}(x,y) = (y+x^2\cos{x}, 2x-y^2\sin{y}). Calcule \oint\limits_{C}{F(P).dP} sendo C o círculo com centro na origem e raio 1.

SOLUÇÃO: 

Leia Mais:

• Integral de Linha de 1ª Espécie | 1ª Lista de Exercícios Resolvidos
• Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano
• Integral de Superfície | Campos Escalares, Campos Vetoriais e Fluxos

Assista Nossa Vídeo-Aula Sobre Integral de Campos Vetoriais