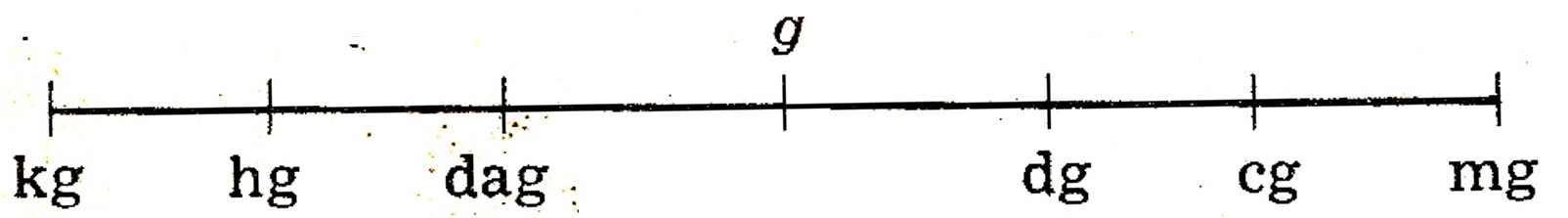Sistema Decimal de Medidas: Comprimento, Área, Massa e Volume

Descubra o fascinante mundo das medidas com nosso guia detalhado sobre o Sistema Decimal de Medidas! Aprofunde-se nas unidades de comprimento, área, volume e massa, e entenda como a matemática simplifica a vida cotidiana.

Introdução

Unidades e Medidas de Comprimento

Múltiplos e sub-múltiplos do sistema métrico:

Kilo significa 1.000 vezes,
Hecta significa 100 vezes,
Deca significa 10 vezes,
Deci significa décima parte,
Centi significa centésima parte,
Mili significa milésima parte.

$1 \text{ km} = 1000 \text{ m}$
$1 \text{ hm} = 100 \text{ m}$
$1 \text{ dam} = 10 \text{ m}$

$1 \text{ m} = 10 \text{ dm}$
$1 \text{ m} = 100 \text{ cm}$
$1 \text{ m} = 1000 \text{ mm}$

Transformações de unidades:

$45 \text{ Km} = 45 \cdot 1000 = 45,000 \text{ m}$
$500 \text{ cm} = 500 \div 100 = 5 \text{ m}$
$8 \text{ Km e } 25 \text{ m} = 8000 \text{ m} + 25 \text{ m} = 8025 \text{ m} \text{ ou } 8.025 \text{ Km}$

Unidades e Medidas de Área

Metro quadrado:Propriedade:

Múltiplos e sub-múltiplos do metro quadrado:

$1 \text{ km}^2 = 1000000 \text{ m}^2$
$1 \text{ hm}^2 = 10000 \text{ m}^2$
$1 \text{ dam}^2 = 100 \text{ m}^2$

$1 \text{ m}^2 = 100 \text{ dm}^2$
$1 \text{ m}^2 = 10000 \text{ cm}^2$
$1 \text{ m}^2 = 1000000 \text{ mm}^2$

Regras Práticas:

Unidades de Volume e Capacidade

Unidades de volume:Propriedade:

Múltiplos e sub-múltiplos do metro cúbico:

$1 \text{ km}^3 = 1000000000 \text{ m}^3$
$1 \text{ hm}^3 = 1000000 \text{ m}^3$
$1 \text{ dam}^3 = 1000 \text{ m}^3$

$1 \text{ m}^3 = 1000 \text{ dm}^3$
$1 \text{ m}^3 = 1000000 \text{ cm}^3$
$1 \text{ m}^3 = 1000000000 \text{ mm}^3$

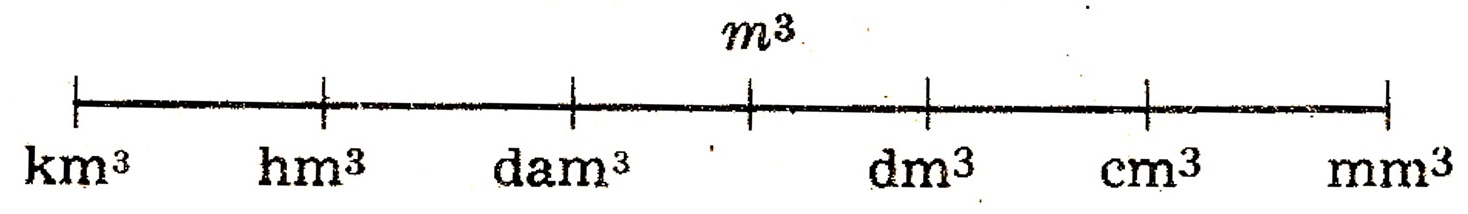Unidades de capacidade:

Apoie Nosso Trabalho:

Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697

$1 \text{ hl} = 100 \text{ l}$
$1 \text{ dal} = 10 \text{ l}$

$1 \text{ l} = 10 \text{ dl}$
$1 \text{ l} = 100 \text{ cl}$
$1 \text{ l} = 1000 \text{ ml}$

Unidade de Massa

Múltiplos e sub-múltiplos do kilograma:

$1 \text{ kg} = 1000 \text{ g}$
$1 \text{ hg} = 100 \text{ g}$
$1 \text{ dag} = 10 \text{ g}$

$1 \text{ g} = 10 \text{ dg}$
$1 \text{ g} = 100 \text{ cg}$
$1 \text{ g} = 1000 \text{ mg}$

Sistema Decimal de Medidas: Comprimento, Área, Massa e Volume

Introdução

Unidades e Medidas de Comprimento