Uma função trigonométrica é aquela na forma f(x) = a+b {\rm trig}(cx+d) onde {\rm trig} representa algum objeto trigonométrico como seno, cosseno, tangente, etc. Ou seja, as funções trigonométricas são aquelas que associam ângulos em radianos a números reais.
Ângulos
Ângulos são medidas de quantidade de rotação e alguns deles possuem possuem nomes especiais, se denotarmos um ângulo qualquer por \alpha teremos:
- Ângulo Agudo: se 0° < \alpha < 90°;
- Ângulo Reto: \alpha = 90°;
- Ângulo Obtuso: se 90º < \alpha < 180°;
- Ângulo Raso: se \alpha = 180°.
Não existe um limite superior à quantidade de rotação, sendo 360° o ângulo correspondente a uma rotação completa.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Radianos
Para as funções trigonométricas usamos a medida radianos para os ângulos, pois assim, podemos associar todos os ângulos a um domínio real. O radiano pode ser associado com a medida em graus por uma simples relação \pi rad = 180°. A medida de um radiano corresponde à aproximadamente 57,295° e a medida de 1 grau corresponde à aproximadamente 0,01745 radianos.
Alguns ângulos são mais utilizados e por esta razão são conhecidos como ângulos notáveis. São eles: $$30° = \frac{\pi}{6}; 45° = \frac{\pi}{4}; 60º = \frac{\pi}{3}.$$ Para eles existem uma tabela muito conhecida que relaciona os senos, cossenos e tangente de seus ângulos.
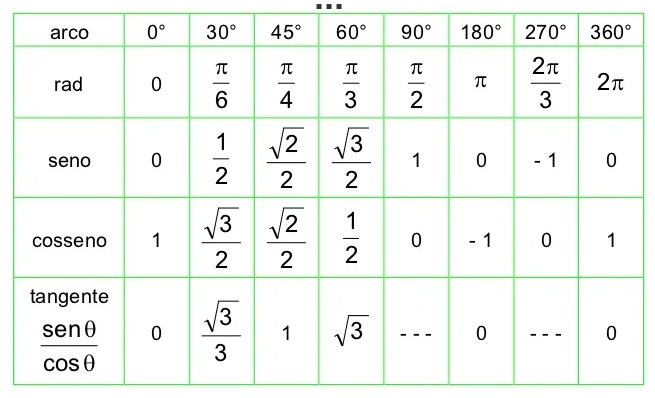 Tabela de Ângulos Notáveis
Tabela de Ângulos Notáveis
PROPRIEDADES:
- O seno é positivo no primeiro e segundo quadrantes e negativo no terceiro e quarto quadrantes.
- O cosseno é positivo no primeiro e quarto quadrantes e negativo no segundo e terceiro quadrantes.
- O seno e cosseno são funções 2\pi-periódicas com imagem no intervalo [-1,1].
- O cosseno é uma função par e o seno é uma função ímpar.
- {\rm sen}\,{t}=\cos\left({\dfrac{\pi}{2}-t}\right) e \cos{t}={\rm sen}\left(\dfrac{\pi}{2}-t\right).
- -{\rm sen}\,{t}=\cos\left({\dfrac{\pi}{2}+t}\right) e \cos{t}={\rmsen}\left(\dfrac{\pi}{2}+t\right).
- {\rm sen}\,{t}={\rm sen}(\pi-t) e -\cos{t}=\cos(\pi-t).
- -{\rm sen}\,{t}={\rm sen}(\pi+t) e -\cos{t}=\cos(\pi+t).
- {\rm sen}(0)=\cos\left(\dfrac{\pi}{2}\right)=0 e \cos(0)={\rm sen}\left(\dfrac{\pi}{2}\right)=1.
A Trigonometria do Triângulo Retângulo.
Consideremos um triângulo ABC, retângulo em \hat{B}, como na figura abaixo.
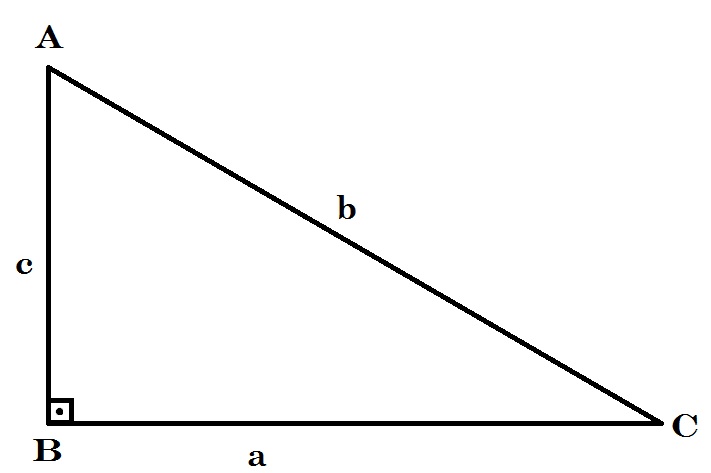
Desta forma, em relação ao ângulo \hat{C}, podemos estabelecer que
- \overline{BC} é o cateto adjacente, de medida a;
- \overline{AB} é o cateto oposto, de medida c;
- \overline{AC} é a hipotenusa, de medida b.
Nestas condições, definimos as seguintes relações trigonométricas: $$\sin{\hat{C}} = \frac{c}{b},$$ $$\cos{\hat{C}} = \frac{a}{b}$$ e $$\tan{\hat{C}} = \frac{c}{a} = \frac{\sin{\hat{C}}}{\cos{\hat{C}}}.$$
DUAS RELAÇÕES IMEDIATAS: Estas relações trigonométricas não são independentes e duas relações aparecem naturalmente:
- \tan{\hat{C}} = \dfrac{\sin{\hat{C}}}{\cos{\hat{C}}}.
- \sin^2{x}+\cos^2{x} = 1.
FÓRMULAS DE ADIÇÃO E DA TRANSFORMAÇÃO DO PRODUTO EM SOMA:
Valendo-nos de propriedades geométricas obtemos as seguintes relações:
- \cos(x+y) = \cos{x} \cos{y} - sen(x) \sin{y};
- \sin(x+y) = sen(x) \cos{y} + \cos{x} \sin{y};
- \tan(x+y) = \dfrac{\tan{a}+\tan{b}}{1 - \tan{a}\tan{b}};
- \tan(x-y) = \dfrac{\tan{a}-\tan{b}}{1 + \tan{a}\tan{b}}.
- \cos(\alpha)\cos(\beta)=\frac{1}{2} \cos(\alpha+\beta)+\frac{1}{2}\cos(\alpha-\beta).
- {\rm sen}(\alpha){\rm sen}(\beta)=\frac{1}{2}\cos(\alpha+\beta)-\frac{1}{2} \cos(\alpha-\beta).
- {\rm sen}(\alpha)\cos(\beta)=\frac{1}{2}\,{\rm sen}(\alpha+\beta)-\frac{1}{2} \,{\rm sen} (\alpha-\beta).
- {\rm sen}\,(\alpha) +{\rm sen}\,(\beta)=2 {\rm sen}\Bigl (\frac{\alpha+\beta}{2}\Bigl)\cos\Bigl(\frac{\alpha-\beta}{2}\Bigr) .
- \cos(\alpha) +\cos(\beta)=2 \cos\Bigl(\frac{\alpha+\beta}{2}\Bigr)\cos\Bigl(\frac{\alpha-\beta}{2}\Bigl).
FÓRMULAS DO ARCO DUPLO E DO ARCO METADE:
- \cos(2\alpha)=\cos^2(\alpha)-{\rm sen}^2(\alpha).
- {\rm sen}(2\alpha)= 2\,{\rm sen}(\alpha)\cos(\alpha).
- \cos(\alpha)=\pm\sqrt{\dfrac{1+\cos(2\alpha)}{2}}.
- {\rm sen}(\alpha)=\pm\sqrt{\dfrac{1-\cos(2\alpha)}{2}}.
O Círculo Trigonométrico
Para as funções trigonométricas utilizamos o círculo trigonométrico para representar os ângulos. Este é um círculo unitário centrado na origem do plano cartesiano, de modo que os ângulos são marcados em sentido anti-horário. Ângulos podem ser negativos e no círculo trigonométrico eles são marcados no sentido anti-horário. Abaixo uma demonstração de como os ângulos estão relacionados no círculo trigonométrico.
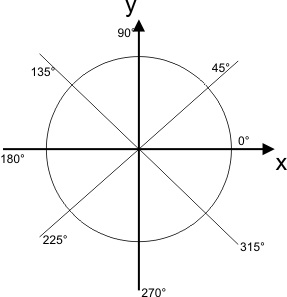 O Círculo Trigonométrico
O Círculo Trigonométrico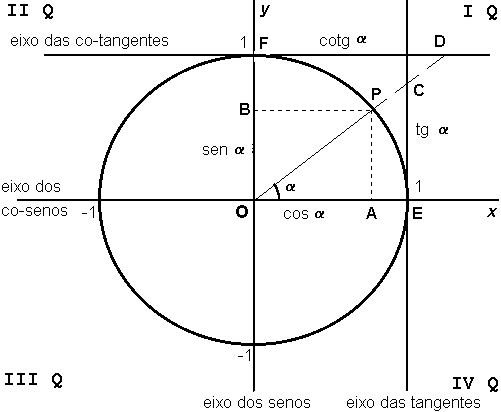
A Função Seno
Seja x um número real. A função seno é aquela que associa a cada número real x ao seno de x radianos. Ou seja, $$f(x) = sen{x}.$$ O domínio de sen(x) é o conjunto real e a imagem é o conjunto [-1,1]. A função seno é 2\pi-periódica, ou seja, $$sen{(x+2k\pi)} = sen{(x)};\;\;\;\forall k=1,2,3,4,5,…$$ e para qualquer x \in \mathbb{R}, $$sen{(-x)} = sen{x}.$$As raízes de sen{x} são k\pi.
O gráfico da função sen{x} é denominado senóide e é dado por:
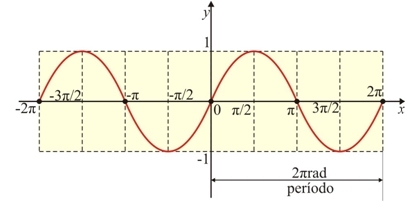 Gráfico da Função Seno
Gráfico da Função Seno
A Função Cosseno
Seja x um número real. A função cosseno é aquela que associa a cada número real x ao cosseno de x radianos. Ou seja, $$f(x) = \cos{x}.$$
O domínio de \cos{x} é o conjunto real e a imagem é o conjunto [-1,1] e as raízes de \cos{x} são \dfrac{\pi}{2} +k\pi.
A função cosseno é 2\pi-periódica, ou seja, $$\cos{(x+2k\pi)} = \cos{(x)};\;\;\;\forall k=1,2,3,4,5,…$$ e para qualquer x\in \mathbb{R}, $$\cos{(-x)} = \cos{x}.$$
O gráfico da função \cos{x} é denominado cossenóide e é dado por:
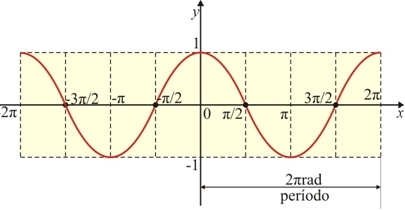 Gráfico da Função Cosseno
Gráfico da Função Cosseno
A Função Tangente
Seja x um número real. A função tangente é aquela que associa a cada número real x à tangente de x radianos. Ou seja, $$f(x) = \tan{x}.$$
O domínio de \tan{x} é o conjunto real ecluindo as raízes do cosseno e a imagem é o conjunto real. A função tangente satisfaz a propriedade \tan{(x)} = \tan{(x +\pi)}a e as raízes de \tan{x} são x = k\pi.
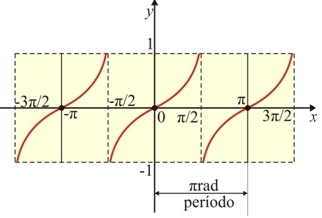
O gráfico da função \tan{x} é dado por:
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
A Função Cossecante
Seja x um número real. A função cossecante é aquela que associa a cada número real x à cossecante de x radianos. Ou seja, $$f(x) = cossec{x},$$ onde $$cossec{x} = \frac{1}{sen(x)}$$
O domínio de cossec{x} é o conjunto real excluindo as raízes do seno e a imagem é o conjunto real. A função cossecante é 2\pi-periódica e não admite raíz.
A Função Secante
Seja x um número real. A função secante é aquela que associa a cada número real x à secante de x radianos. Ou seja, $$f(x) = sec{x},$$ onde $$sec{x} = \frac{1}{\cos{x}}.$$
O domínio de sec{x} é o conjunto real excluindo as raízes do cosseno e a imagem é o conjunto real. A função secante é 2\pi-periódica e também não admite raíz.
A Função Cotangente
Seja x um número real. A função cotangente é aquela que associa a cada número real x à cotangente de x radianos. Ou seja, $$f(x) = cotg{x},$$ onde $$cotg{x} = \frac{1}{\tan{x}} = \frac{\cos{x}}{sen(x)}.$$
O domínio de cotg{x} é o conjunto real excluindo as raízes do seno e a imagem é o conjunto real. A função cotangente é 2\pi-periódica e as raízes são iguais às raízes da função cosseno.
Gráficos das funções Cotangente, Cossecante e Secante
O gráfico das funções cossecante, secante e cotangente são dados na figura abaixo:
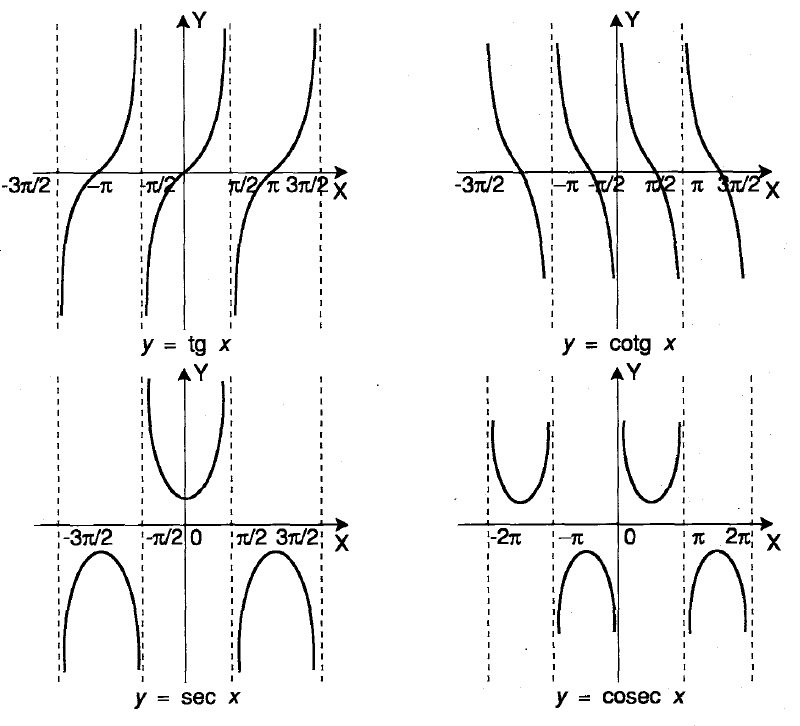 Gráfico das funções trigonométricas: tangente, secante, cossecante e cotangente
Gráfico das funções trigonométricas: tangente, secante, cossecante e cotangente



Pingback: Funções Exponenciais | Funções Reais (Pré-Cálculo) - Matemática Simplificada
Pingback: Funções Exponencial e Logarítmica | Pré-Cálculo