Denominamos função exponencial de base a, a função que associa cada x real, o número a^x, sendo a>0, a\neq 1. O domínio de toda função exponencial é o conjunto \mathbb{R} e a imagem o conjunto (0,+\infty). Ela não admite raíz real.
Vejamos o que isso significa.
- Se x = n , um inteiro positivo, então a^n = \underbrace{aa \cdots a}_{n \, vezes}.
- Se x = 0, então a^0 = 1.
- Se x = -n , onde n é um inteiro positivo, então a^{-n}= \dfrac{1}{a^n}.
- Se x = \dfrac{p}{q} , onde p e q são inteiros e q > /0, então a^{p/q} = \sqrt[q]{a^p} = (\sqrt[q]{a})^p.
- Se x for um número irracional. Considere o caso a > 1, então a^x é o único número real cujas aproximações por falta são as potências a^r, com r racional menor do que x e cujas aproximações por excesso são as potências a^s , com s racional maior do que x. Em outras palavras, a^x satisfaz a seguinte propriedade: $$ r < x < s, \quad \text{com} \quad r,\,s \in \quad \Longrightarrow \quad a^r < a^x < a^s.$$ Se a < 1, a^x satisfaz: $$ r < x < s, \quad \text{com} \quad r,\,s \in \quad \Longrightarrow
\quad a^s < a^x < a^r.$$ Desta forma, se olhamos o gráfico da função a^x onde x racional, os buracos correspondentes aos valores irracionais de x , foram preenchidos de forma a obter uma função crescente para todos os números reais.
O Gráfico da Função Exponencial
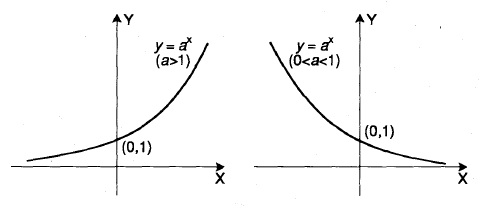 Gráfico da Função Exponencial
Gráfico da Função Exponencial
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Propriedades da Exponencial
Sejam a e b números positivos e x e y números reais quaisquer, então
- a^{x+y} = a^x a^y,
- (a^x)^y = a^{xy},
- (ab)^x = a^x b^x,
- Se a > 1 a função exponencial é estritamente crescente, ou seja, se x < y então a^x < a^y .
- Se 0 < a < 1 a função exponencial é estritamente decrescente, ou seja, se x < y então a^x > a^y .
A FUNÇÃO LOGARÍTMICA
Como a função exponencial é ou crescente ou decrescente, existe a função inversa. A função inversa da função exponencial é chamada função logarítmica com base a e denotada por \log_a. Assim, $$ \log_a x = y \quad \Longleftrightarrow \quad a^y=x.$$
Note que \log_a x está definido para x > 0,\, a > 0 e a \neq 1. Além disso satisfaz $$ \log_a(a^x) = x ,\, x \in \mathbb{R} \qquad e \qquad a^{\log_a x} = x ,\, x >0.$$
O Gráfico da Função Logarítmica
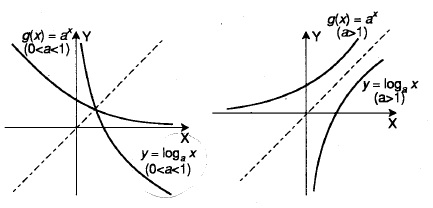
Propriedades do Logaritmo
Sejam a > 0 ,\, a \neq 1,\, b > 0,\, b\neq 1. Então são válidas as seguintes propriedades
- \log_a x y = \log_a x + \log_a y ,
- \log_a x^y = y \log_a x,
- \log_a \dfrac{x}{y} = \log_a x - \log_a y,
- Se a > 1 a função logarítmica é estritamente crescente, ou seja, se x < y, então \log_a x < \log_a y,
- Se 0 < a < 1 a função logarítmica é estritamente decrescente, ou seja, se x < y, então \log_a x > \log_a y,
- (Mudança de base) \log_a x = \dfrac{\log_b x}{\log_ba}.
Uma Função Exponencial Especial e o Logaritmo Natural
A função exponencial de base e onde e \approx 2,718281 ,\, f(x) = e^x , desempenha um papel importante no cálculo. A função logarítmica com base e é chamada logaritmo natural e denotada por \log_e x= \ln x.
Observe que como \ln(e^x) = x, tomando x = 1 temos que \ln e = 1.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Há varias formas de introduzir o número e. Uma delas é mostrar que o número e é um irracional que pode ser escrito como o limite de uma sequência de números reais dada por $$e = \lim_{n \rightarrow \infty}{\left( 1 + \frac{1}{n} \right)^n} = 2.71828182846…$$ Este limite resultado determina um importante limite envolvendo funções exponenciais, chamado de 2º Limite Fundamental.
A função logarítmica com base e é chamada logaritmo natural e denotada por \log_e x= \ln x. Observe que como \ln(e^x) = x, tomando x = 1 temos que \ln e = 1. No cálculo pode-s-e definir o logaritmo natural utilizando integrais e , nesse caso, o número e será o único número satisfazendo \ln e =1.


