Nesse artigo, queremos desenvolver conceitos básicos e teóricos e das equações diferenciais de primeira ordem, principalmente o Teorema de Existência de Unicidade de Soluções. Em geral, uma equação diferencial ordinária de primeira ordem é representada por \dfrac{dy}{dt}= f\left(t,y \right) onde f é uma função nas variáveis t e y. Nosso problema consiste em: Dada f\left(t,y \right), encontre funções y(t) que satisfaçam essa equação.
O que garante a existência de tais soluções é o teorema da existência e unicidade de soluções para equações diferenciais de primeira ordem, que sob certas condições asseguram a existência de um intervalo que tal solução está definida.
Problema de Valor Inicial
Queremos resolver uma equação diferencial de primeira ordem \dfrac{dy}{dt}= f\left(t,y \right), onde f é uma função nas variáveis t e y, sujeita à condição inicial y(t_0) = y_0 em que t_0 é um número no intervalo I e y_0 é um número real arbitrário.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Esse problema é chamado de Problema de Valor Inicial.
Em termos geométricos, estamos procurando uma solução para a equação diferencial, definida em algum intervalo I tal que o gráfico da solução passe por um ponto (x_0 , y_0) determinado à priori.
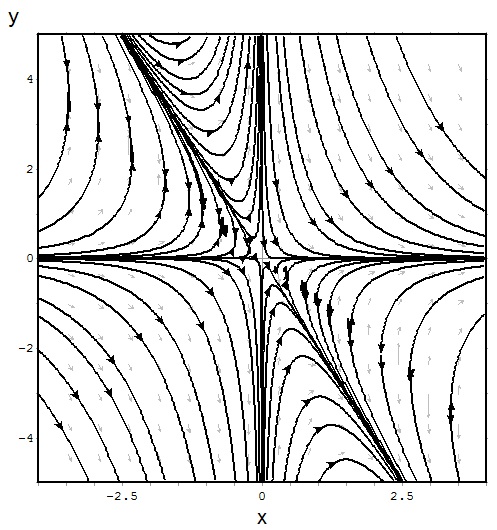
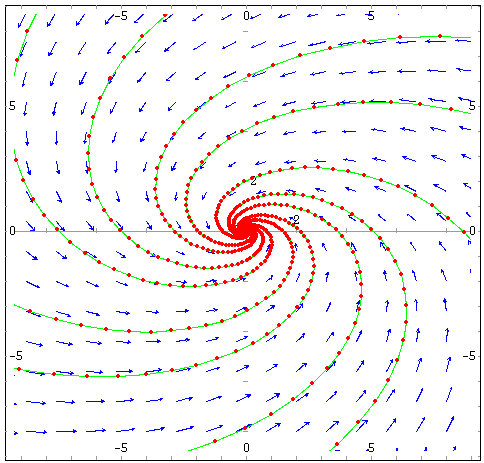 Em cada ponto do plano (t, y) temos um solução da EDO. Em cada trajetória temos uma solução de um P.V.I.
Em cada ponto do plano (t, y) temos um solução da EDO. Em cada trajetória temos uma solução de um P.V.I.
Teorema da Existência e Unicidade de Solução
Em geral, deseja-se saber,a ntes de considerar um problema de valor inicial, se uma solução existe e, quando existe, se é a única solução para o problema.
O teorema abaixo, devido a Charles Émile Picard, nos dá condições suficientes para garantir existência e unicidade de soluções.
TEOREMA
Seja R uma região retangular no plano ty definida por a\leq t \leq b, \;\;\; c \leq y \leq d , que contém o ponto (t_0, y_0) em seu interior. Se f(t ,y) e \dfrac{\partial f}{\partial y} são contínuas em R, então existe um intervalo I centrado em t_0 e uma única função y(t) definida em I que satisfaz o problema de valor inicial \dfrac{dy}{dt}= f\left(t,y \right)\;\;\; y(t_0) = y_0
O resultado anterior é um dos mais populares teoremas de existência e unicidade para equações de primeira ordem, porque os critérios de continuidade de f(t, y) e \dfrac{\partial f}{\partial y} são relativamente fáceis de ser verificados.
OBSERVAÇÕES:
- A garantia de existência não significa conseguir exibir a solução do P.V.I., uma solução pode existir e não ser possível expressá-la por funções elementares, apenas por métodos numéricos.
- As condições do Teorema de Existência e Unicidade são suficientes, mas não necessárias.
Plano de Fase
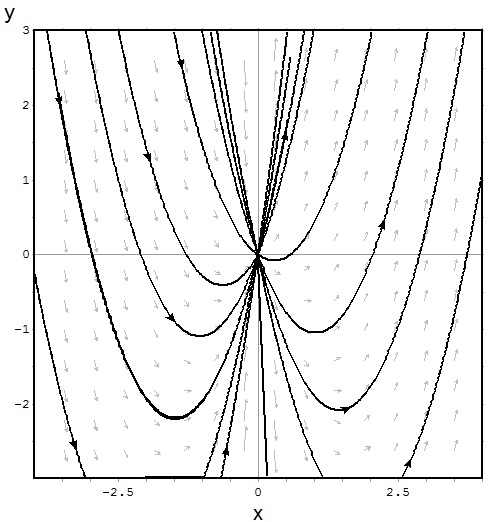
EXEMPLOS DE PLANOS DE FASE DE EDO’S DE 1ª ORDEM
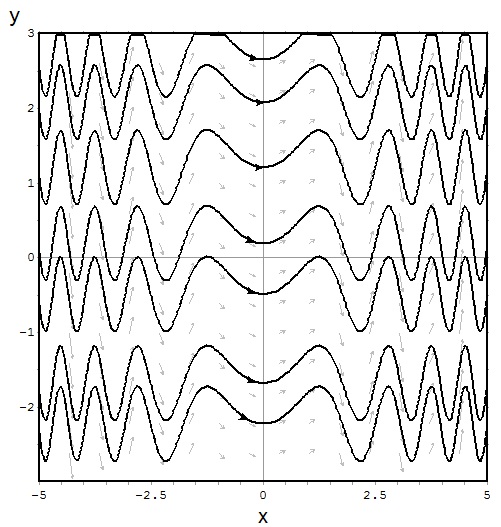
$$\frac{dy}{dt}=\frac{t^2}{y^2}$$
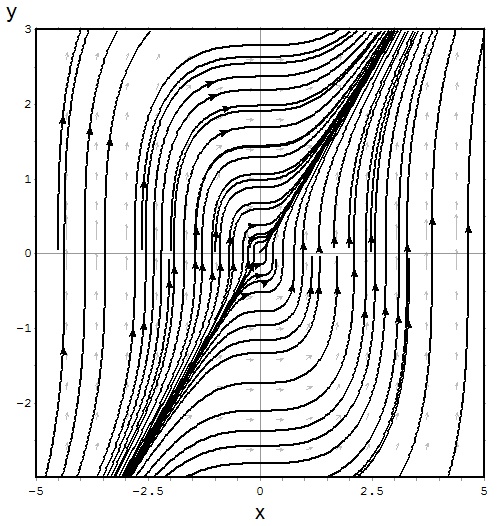
$$\frac{dy}{dt}=\frac{t^2}{1-y^2}$$
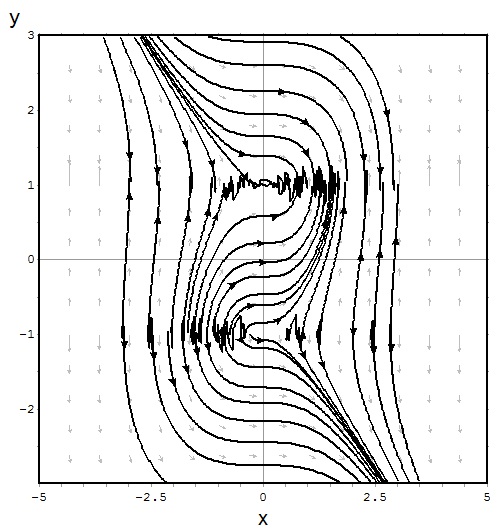
$$\frac{dy}{dt}=\frac{3t^2+4t+2}{2(y-1)}$$
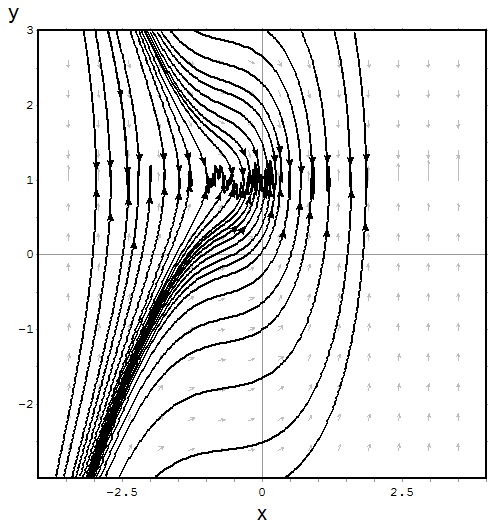
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
$$t \frac{dy}{dt} + 2y = 4t^2$$
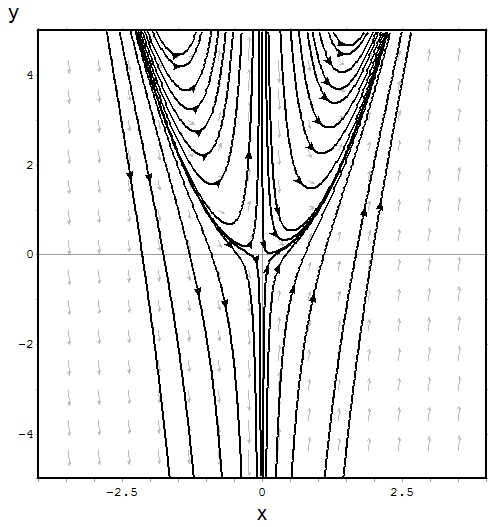
$$\left( y\cos{x}+2xe^y\right) + \left( \sin{x} + x^2e^y-1 \right)y’=0$$
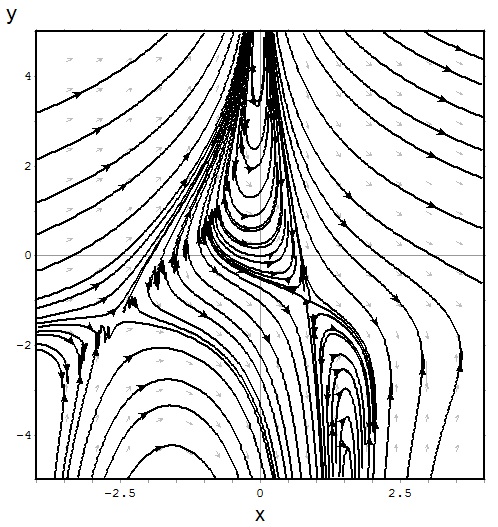
$$\left( 3xy + y^2 \right)+ \left(x^2 + xy\right)y’=0$$