Curvas no Espaço | Deslocamento de Partícula

As curvas são um objeto matemático importante no estudo da física, pois a representação dada por f(t) = x(t) \vec{i} + y(t) \vec{j} + z(t) \vec{k} é chamata de representação paramétrica da curva C e este tipo de representação é útil em várias aplicações, por exemplo, em mecânica onde a variável t pode ser o tempo.

A função f(t) também pode ser referenciada como vetor posição, pois para cada instante t, f(t) denota a posição de f quando se trata do movimento de uma partícula.

Considere o vetor \vec{f} (t) = (x(t), y(t), z(t) como o vetor posição da partícula com relação a um sistema de coordenadas cartesianas tridimensionais, em relação ao tempo t.

O vetor \vec{v} (t) = \vec{f'} (t) é a velocidade instantânea da partícula no tempo t, quando o limite que define esta derivada existe.

Quando \vec{v} (t) admite derivada, então \vec{a} (t) = \vec{v'} (t) = \vec{f''} (t) será a aceleração da partícula.

Suponhamos que uma partícula se desloca no espaço de modo que no instante t, t \in [0. b), a sua posição dada em forma paramétrica por x=x(t),y=y(t) e z=z(t), com \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} contínuas.

Então, o espaço s=s(t) percorrido pela partícula entre os instantes 0 e t nada mais é do que o comprimento da curva descrita pela partícula entre estes instantes, ou seja, $$s=\int_0^t{\sqrt{\left( \frac{dx}{dt} \right) ^2+ \left(\frac{dy}{dt}\right) ^2 + \left(\frac{dz}{dt}\right) ^2}}dt.$$

Por consequência, a velocidade desta partícula pode ser dada por $$\frac{ds}{dt} = \sqrt{\left( \frac{dx}{dt} \right) ^2+ \left(\frac{dy}{dt}\right) ^2 + \left(\frac{dz}{dt}\right) ^2}$$

EXEMPLO

Uma partícula desloca-se no espaço com equações paramétricas x=x(t),y=y(t) e z=z(t). Sabe-se que para todo t, $$\frac{dx}{dt}=\sqrt{2}, \frac{dy}{dt}=\sqrt{2},\frac{dz}{dt}(0)=2, \frac{d^2z}{dt^2}=-2$$ e que no instante t=0 a partícula encontra-se na origem.

1) Qual posição da partícula no instante t?

• \frac{dx}{dt}=\sqrt{2} \Rightarrow x(t)= \sqrt{2}t + K_1, como x(0) = 0, então K_1 = 0.
• \frac{dy}{dt}=\sqrt{2}\Rightarrow x(t)= \sqrt{2}t + K_2, como y0) = 0, então K_2 = 0
• \frac{d^2z}{dt^2}=-2\Rightarrow \frac{dz}{dt}(t)= -2t + K_3, como \frac{dz}{dt}(0)=2 = 0, então K_3 = 2. Ainda temos que \frac{dz}{dt}(t)= -2t + 2 \Rightarrow z(t) = -t^2 + 2t + K_4, como x0) = 0, então K_4 = 0.

Portanto, a posição da partícula no instante t é $$\left( \sqrt{2}t, \sqrt{2}t, -t^2 + 2t \right).$$

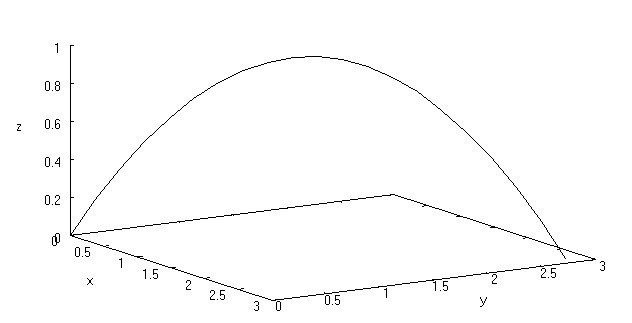
2) Qual a velocidade escalar da partícula?

A velocidade escalar é a derivada do espaço s(t) no instante t.

$$s(t) = \int_0^t{\sqrt{\left( \sqrt{2} \right) ^2+ \left(\sqrt{2}\right) ^2 + \left(-2t + 2 \right) ^2}}dt.$$ Logo,

$$\frac{ds}{dt} = \sqrt{4 + \left(-2t + 2 \right) ^2}$$

3) Determine o instante T em que a partícula volta a tocar o plano xy.

z=0 \Leftrightarrow -t^2 + 2t =0 \Leftrightarrow t=0 \;\;ou\;\; t=2.

Em t=0 a partícula esta saindo do plano xy, mas em T=2 ela está voltando para o plano xy.

EXEMPLO:

Uma partícula se move partindo da posição inicial \vec{r} (0) = (1,0,0) e com velocidade inicial dada por \vec{v}(0) = (1,-1,1). Sua aceleração é \vec{a} (t) = (4t, 6t, 1). Determine sua posição e sua velocidade no tempo t.

SOLUÇÃO: Desde que \vec{a} (t) = \vec{v} ' (t) , nós temos $$ \vec{v} (t) = \int{\vec{a} (t) dt} = \int{(4t\vec{i} + 6t \vec{j} + \vec{k})dt } = 2t^2\vec{i} + 3t^2 \vec{j} + t \vec{k} + \vec{C}.$$

Para determinar o valor do vetor constante \vec{C} , usamos o fato de que \vec{v} (0) = (1,-1,1) . Como

$$ \vec{v} (0) = 2\times 0^2\vec{i} + 3\times 0^2 \vec{j} + 0 \times \vec{k} + \vec{C} = (1,-1,1) \Leftrightarrow \vec{C} = (1,-1,1)$$ Portanto,  $$ \vec{v} (t) = (2t^2 +1) \vec{i} + (3t^2 -1) \vec{j} + (t + 1) \vec{k}.$$

Agora, como \vec{v} (t) = \vec{r} ' (t) , nós temos $$ \vec{r} (t) = \int{ \vec{v} (t) dt} = \left( \frac{2}{3} t^3 +t \right) \vec{i} + \left( t^3 – t \right) \vec{j} + \left( \frac{1}{2} t^2 +t \right) \vec{k} + \vec{D}$$

Fazendo t = 0 , encontramos \vec{D} = \vec{r} (0) = \vec{i} , portanto $$ \vec{r} (t) = \left( \frac{2}{3} t^3 +t +1 \right) \vec{i} + \left( t^3 – t \right) \vec{j} + \left( \frac{1}{2} t^2 +t \right) \vec{k}.$$

Leia Mais:

• Curvas no Espaço | Parametrização de Curvas Clássicas
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Curvas no Espaço | 5ª Lista de Exercícios Resolvidos
• Curvas no Espaço | 4ª Lista de Exercícios Resolvidos

Assista Nossa Vídeo-Aula Sobre o Tema: