Este artigo reúne seis exercícios resolvidos sobre curvas no espaço, como catenária, hélice e circunferência inclinada. Explora parametrização, comprimento de arco, função vetorial e geometria em \( \mathbb{R}^3 \). Ideal para fixar conceitos do cálculo vetorial com aplicações práticas e resolução detalhada de curvas tridimensionais.

Introdução
Curvas no espaço são essenciais no estudo do cálculo vetorial e da geometria analítica tridimensional. Neste artigo, apresentamos 6 exercícios resolvidos que envolvem parametrização, cálculo de comprimento de arco e análise vetorial.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
Com foco em aplicações práticas e conceitos como catenária, hélice e reparametrização, esta lista é ideal para estudantes que desejam fortalecer sua base em \mathbb{R}^3 . Cada solução é explicada passo a passo, facilitando a compreensão e o domínio técnico.
Explore agora como curvas vetoriais ganham vida com matemática aplicada e desenvolva seu raciocínio espacial com exemplos claros e objetivos. Nesse artigo queremos apresentar uma terceira lista de exercícios resolvidos sobre o tema que foram usados como questões de prova no segundo semestre de 2021.
Fundamentação Teórica
O estudo de curvas no espaço tridimensional \( \mathbb{R}^3 \) parte da definição de uma função vetorial que representa a posição de um ponto em movimento. Essa curva é descrita por:
\[
\vec{r}(t) = x(t)\, \hat{i} + y(t)\, \hat{j} + z(t)\, \hat{k}
\]
onde \( x(t) \), \( y(t) \) e \( z(t) \) são funções contínuas que definem as coordenadas do ponto em relação ao parâmetro \( t \).
Dizemos que uma curva é regular quando sua derivada vetorial \( \vec{r}'(t) \) existe, é contínua e diferente de zero para todo \( t \) no intervalo considerado. A derivada da função posição é dada por:
\[
\vec{r}'(t) = x'(t)\, \hat{i} + y'(t)\, \hat{j} + z'(t)\, \hat{k}
\]
Esse vetor é tangente à curva e tem aplicações diretas na análise de velocidade e direção do movimento.
O comprimento de arco de uma curva vetorial entre os pontos \( t = a \) e \( t = b \) é calculado pela integral:
\[
L = \int_a^b \left\| \vec{r}'(t) \right\| \, dt
\]
com
\[
\left\| \vec{r}'(t) \right\| = \sqrt{(x'(t))^2 + (y'(t))^2 + (z'(t))^2}
\]
Essa fórmula mede a extensão real da curva no espaço e é fundamental na geometria diferencial e no cálculo vetorial.
Curvas no Espaço | 6ª Lista de Exercícios Resolvidos
1) Se a curva plana é representada na forma y = f(x), z = 0 então o comprimento de arco entre x = a e x = b é $$ s = \int_{a}^{b}{\sqrt{1 + (y’)^2}dx}.$$ Calcule o comprimento de arco da catenária $$y = \cosh{(x)}, \qquad z=0, $$ de x = 0 para x = 2 .
SOLUÇÃO: A catenária é uma curva interessante, pois modela o arco formado por uma corrente suspensa apenas pelas duas extremidades. Matematicamente, já foi provado por Jungius, em 1669, que esta curva não é uma parábola. Abaixo, destaco o gráfico de y = \cosh{(x)} :
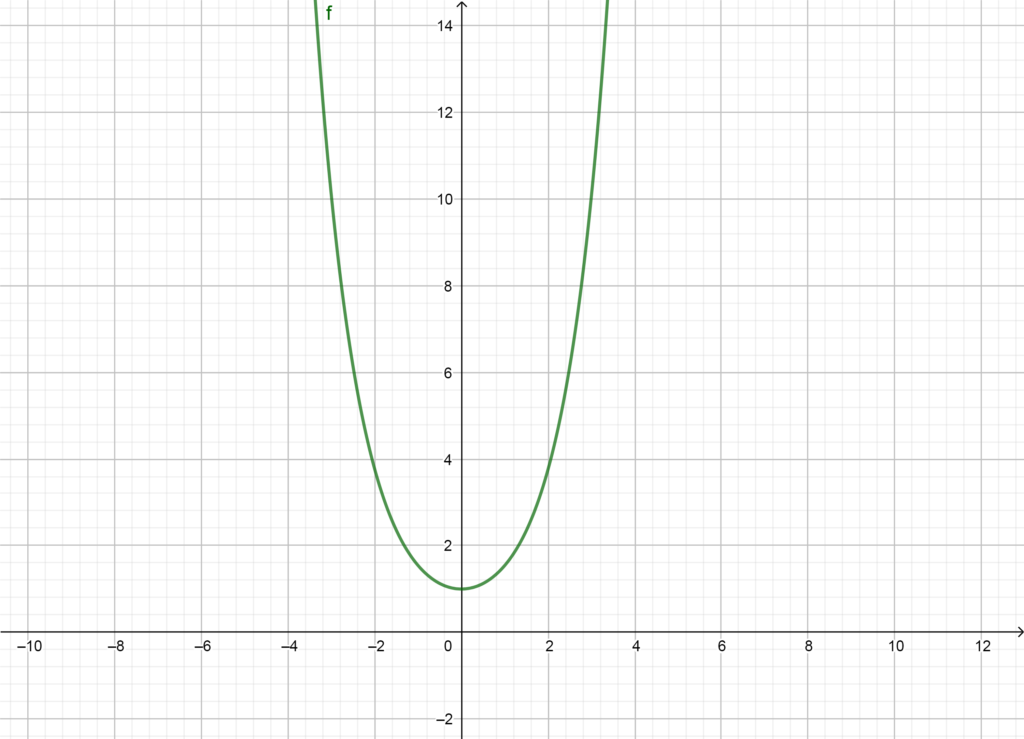 catenária: y(x) = cosh(x)
catenária: y(x) = cosh(x)
Em nosso problema queremos encontrar o comprimento desta curva deitada no espaço sobre o plano z=0, e com a variável x no intervalo [0,2]. Desta forma, usando a fórmula dada no enunciado e lembrando que cosh' (x) = senh(x) , obtemos $$s = \int_{0}^{2}{\sqrt{1 + \left[ (cosh (x))’ \right]^2}dx} = \int_{0}^{2}{\sqrt{1 + senh ^2 (x)}dx}.$$
Lembrando que as funções hiperbólicas satisfazem a relação $$ cosh^2 (x) – senh^2 (x) = 1 \Leftrightarrow cosh^2 (x) = 1 + senh^2(x),$$ então, usando o fato de que \int{cosh(x)dx} = senh(x) +c, encontramos $$s = \int_{0}^{2}{\sqrt{1 + senh ^2 (x)}dx} = \int_{0}^{2}{\sqrt{cosh ^2 (x)}dx} = $$ $$ = \int_{0}^{2}{cosh (x)dx} = \left[ senh(x) \right]^{2}_{0} = senh(2) – senh(0)= 3,63 – 0 = 3,63\;\; u. m.$$ Esta é a medida do arco abaixo:
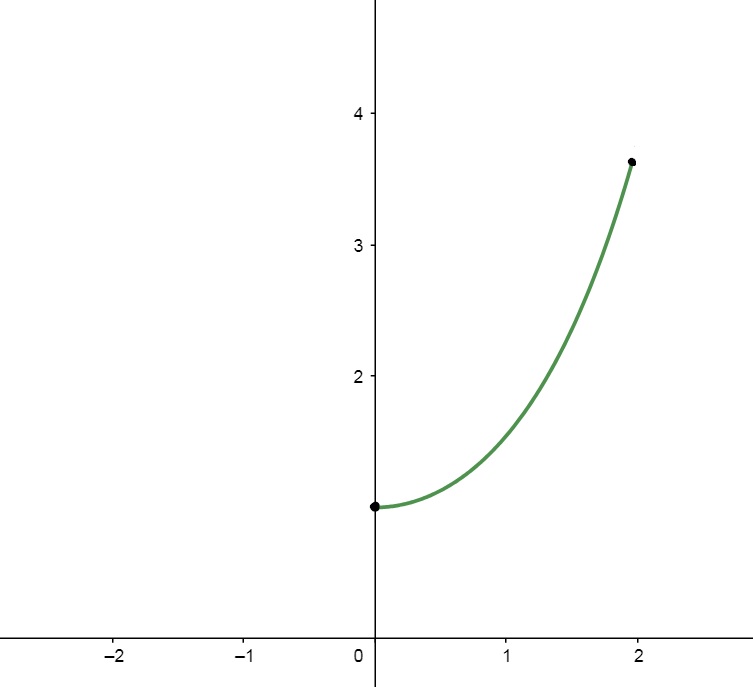
2) Escreva as equações paramétricas da reta tangente da curva $$\vec{r}(t) = 2 cos(t) \vec{i} + sen(t) \vec{j}$$ no ponto P \left( \sqrt{2} , \dfrac{1}{\sqrt{2}} , 0 \right) .
SOLUÇÃO: Sabemos, deste artigo, que a equação da reta tangente à trajetória da função \vec{r}(t) , no ponto \vec{r}(t_0) é dada por $$ s: X = \vec{r}(t_0) + t \vec{r’}(t_0) .$$
Facilmente percebemos que \vec{r}(\pi / 4) = \left( \sqrt{2} , \dfrac{1}{\sqrt{2}} , 0 \right) e, como \vec{r'}(t) = \left( -2sen(t), cos(t), 0\right) , então, \vec{F'}(\pi /4) = \left( -\sqrt{2}, \dfrac{1}{\sqrt{2}}, 0 \right). Portanto, a equação da reta tangente à trajetória da função \vec{r}(t) , no ponto \vec{r}(\pi /4) é $$r: (x,y,z) = \left( \sqrt{2} , \frac{1}{\sqrt{2}} , 0 \right) + t \left( -\sqrt{2}, \frac{1}{\sqrt{2}}, 0 \right); \qquad t \in \mathbb{R}.$$
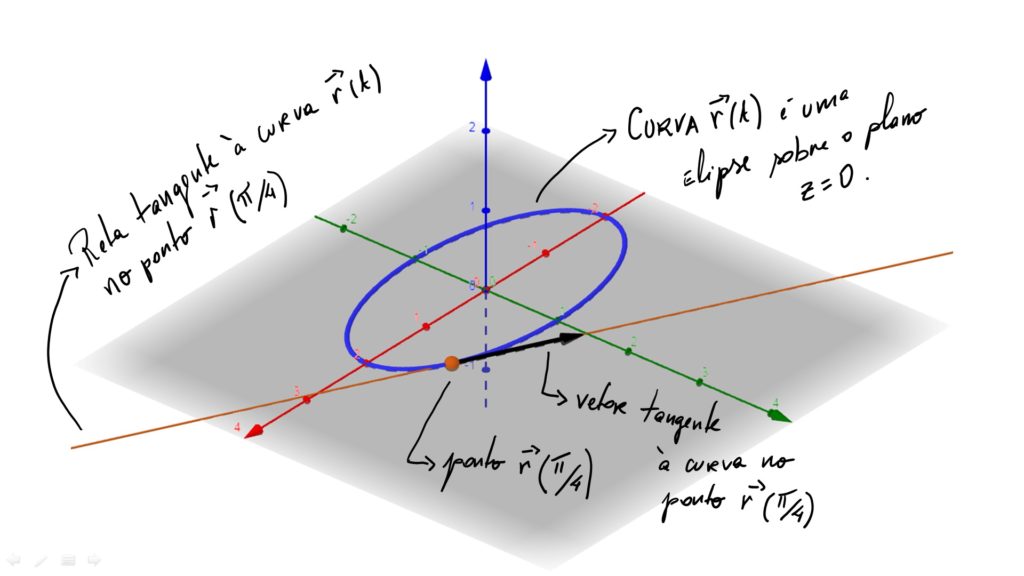
3) Mostre que os vetores velocidade e aceleração do movimento helicoidal $$\vec{P}(t) = (cos(t), sen(t), t)$$ têm comprimentos constantes.
SOLUÇÃO: De fato, os vetores velocidade e aceleração são dados, respectivamente, por $$ \vec{v}(t) = \vec{P’}(t) = (-sen(t), cos(t), 1); \qquad e \qquad \vec{a}(t) = \vec{P”}(t) = (-cos(t), -sen(t), 0).$$ Portanto, $$ |\vec{v}(t)| = \sqrt{[-sen(t)]^2 + [cos(t)]^2 +1} = \sqrt{sen^2 (t) + cos^2 (t) + 1} = \sqrt{2};$$ $$ | \vec{a}(t) | = \sqrt{[-cos(t)]^2 + [-sen(t)]^2 +0} = \sqrt{1} = 1,$$ que são constantes para qualquer do ponto da curva.
4) Indique o intervalo de continuidade da função vetorial $$ \vec{f}(t) = (sen(t), tg(t), e^t).$$
SOLUÇÃO: Note que:
- x(t) = sen(t) é uma função contínua para todo t \in \mathbb{R} .
- y(t) = tg(t) é uma função contínua para todo t \in \mathbb{R} tal que t \neq \dfrac{ \pi}{2} + k \pi, com k \in \mathbb{Z}
- z(t) = e^t é uma função contínua para todo t \in \mathbb{R} .
Desta forma, \vec{f}(t) será contínua na interseção dos intervalos de continuidade de suas funções componentes. Como x(t) e z(t) são contínuas para qualquer t real, então o intervalo de continuidade de \vec{f}(t) será o mesmo de y(t) = tg(t) . Portanto, o intervalo de continuidade de \vec{f}(t) será $$\left\{ t \in \mathbb{R}; t \neq \frac{ \pi}{2} + k \pi, k \in \mathbb{Z} \right\}.$$
5) Calcule o limite $$ \lim_{t \rightarrow 2}{\left( \frac{2^{t-2} -1}{t-2} , \frac{t^2 – 4}{t – 2} , \frac{tg(t-2)}{t-2} \right)} $$
SOLUÇÃO: Observe que:
- Fazendo s = t-2 em x(t) = \dfrac{2^{t-2} -1}{t-2}, obtemos que s \rightarrow 0 quando t \rightarrow 2 , e, assim, usando o corolário do 2º Limite Fundamental: $$ \lim_{t \rightarrow 2}{\frac{2^{t-2} -1}{t-2}} = \lim_{s \rightarrow 0}{\frac{2^{s} -1}{s}} = \ln{2};$$
- Em y(t) = \dfrac{t^2 - 4}{t - 2} podemos usar a regra de L’Hospital e encontrar que $$ \lim_{t \rightarrow 2}{\frac{t^2 – 4}{t-2}} = \lim_{t \rightarrow 2}{2t} = 4 .$$
- Já para z(t) observamos, primeiramente, que $$ \frac{tg(t-2)}{t-2} = \frac{\frac{sen(t-2)}{cos(t-2)} }{t-2} = \frac{sen(t-2)}{(t-2) cos(t-2)} = \frac{sen(t-2)}{(t-2)} \frac{1}{cos(t-2)}.$$ Ou seja, $$ \lim_{t \rightarrow 2}{\frac{tg(t-2)}{t-2}} = \lim_{t \rightarrow 2}{\frac{sen(t-2)}{(t-2)} \frac{1}{cos(t-2)}}$$ e usando o 1º Limite Fundamental encontramos $$ \lim_{t \rightarrow 2}{\frac{tg(t-2)}{t-2}} = \lim_{t \rightarrow 2}{\frac{sen(t-2)}{(t-2)} \frac{1}{cos(t-2)}} = $$ $$ = \lim_{t \rightarrow 2}{\frac{sen(t-2)}{(t-2)}} \lim_{t \rightarrow 2}{ \frac{1}{cos(t-2)}} = 1 \times 1 = 1. $$
Portanto, $$ \lim_{t \rightarrow 2}{\left( \frac{2^{t-2} -1}{t-2} , \frac{t^2 – 4}{t – 2} , \frac{tg(t-2)}{t-2} \right)} = (\ln{2} , 4 , 1).$$
6) Uma curva \vec{r} (t) é chama de simples se ela não possui pontos de auto-interseção. Ou seja, se existirem pontos t_0 e t_1 , tais que \vec{r} (t_0) = \vec{r} (t_1) , a curva não é simples. Considere a curva conhecida como Fólio de Descartes: $$\vec{r}(t)= \frac{3t}{1 + t^3} \vec{i} + \frac{3t^2}{1 + t^3} \vec{j} .$$
a) Esta curva é simples? Se afirmativo, justifique sua resposta mostrando para quais valores de t a curva possui a mesma imagem.
SOLUÇÃO: Esta curva não é simples, como podemos observar no esboço abaixo:
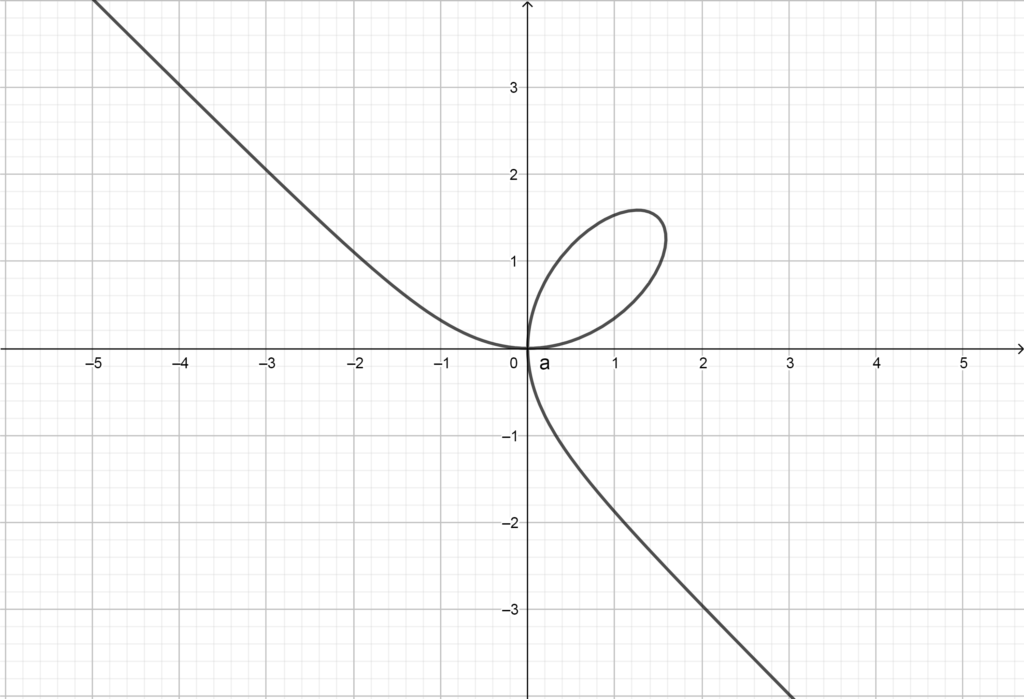 Folium de Descartes
Folium de Descartes
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Podemos ficar tentados a dizer que ela não possui um ponto múltiplo na origem, poiss apenas t=0 tem imagem na origem do sistema. Este fenômeno será explicado pelo item (c).
b) Mostre que todos os pontos desta curva satisfazem a equação cartesiana x^3 + y^3 = 3xy .
SOLUÇÃO: De fato, fazendo x = \dfrac{3t}{1 + t^3} e y = \dfrac{3t^2}{1 + t^3} observamos que $$ x^3 + y^3 = \left( \frac{3t}{1 + t^3} \right)^3 + \left( \frac{3t^2}{1 + t^3} \right)^3 = \frac{27t^3 + 27 t^6}{(1 + t^3)^3} = $$ $$ = \frac{27 t^3 (1 + t^3)}{(1 + t^3)^3} = \frac{27 t^3}{(1 + t^3)^2} = 3 \left( \frac{3t}{1+t^3} \right) \left( \frac{3t^2}{1+t^3} \right) = 3 xy .$$
c) Mostre que quando t \rightarrow \pm \infty a curva tenderá novamente à origem.
SOLUÇÃO: De fato, $$\lim_{t \rightarrow \infty}{\vec{r}(t)} = \vec{i} \lim_{t \rightarrow \infty}{\frac{3t}{1 + t^3}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3t^2}{1 + t^3}} = $$ $$ = \vec{i} \lim_{t \rightarrow \infty}{\frac{3t}{t^3}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3t^2}{t^3}}= \vec{i} \lim_{t \rightarrow \infty}{\frac{3}{t^2}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3}{t}}= (0,0)$$ ou seja, quando o parâmetro tender a \pm \infty o fólio tenderá novamente à origem, e por isso, a continuidade garantirá que a curva possui um ponto múltiplo.
O que acontece é que com t \in ( - \infty , -1) a curva tem um arco que vem na direção da origem ao longo do 4º quadrante, enquanto com t \in ( -1 , + \infty) a curva tem um arco que decresce ao longo do 2º quadrante, corta a origem quanto t = 0 e tende novamente à origem. Obviamente, t = - 1 é um ponto de descontinuidade desta curva. Tentamos ilustrar este comportamento abaixo:
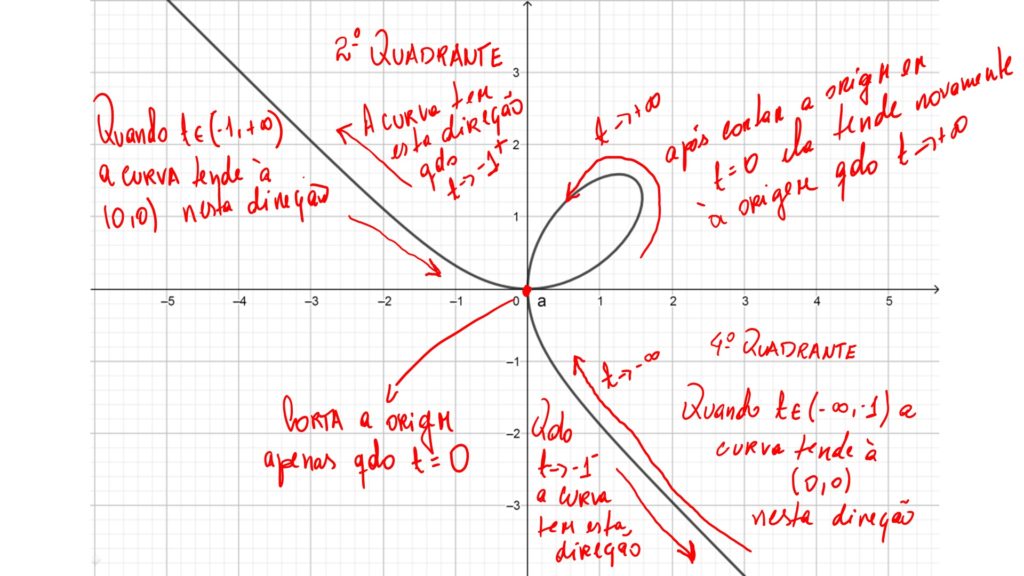
Conclusão:
Ao longo deste artigo, exploramos conceitos fundamentais sobre curvas no espaço tridimensional \mathbb{R}^3 , incluindo parametrização, comprimento de arco e funções vetoriais. Através de seis exercícios resolvidos, abordamos curvas como a catenária, hélice e circunferência inclinada, proporcionando uma compreensão prática e aprofundada desses temas essenciais no cálculo vetorial.
Se você deseja aprofundar seus conhecimentos em cálculo vetorial e dominar a análise de curvas no espaço, convidamos você a conhecer nosso curso completo. Com aulas detalhadas, exercícios práticos e suporte especializado, este curso é ideal para estudantes e profissionais que buscam excelência na área.
👉 Acesse o curso agora e transforme sua compreensão em domínio
Não perca a oportunidade de elevar seu aprendizado a um novo patamar!
Leia Mais:
- Curvas no Espaço | 7ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 5ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 4ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 3ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 2ª Lista de Exercícios Resolvidos
- Curvas no Espaço | 1ª Lista de Exercícios Resolvidos



Pingback: A Catenária | História, Construção Geométrica, Expressão e Comprimento
Pingback: Curvas no Espaço | 7ª Lista de Exercícios Resolvidos