Curvas no Espaço | Operações Elementares de Funções Vetoriais

função vetorialcurva.

FUNÇÕES COMPONENTES

Tais funções são denominadas funções componentes de FEXEMPLOEXEMPLO

1. o domínio de F é o conjunto dos números reais.
2. F(0)=(0,2.0) = (0,0).

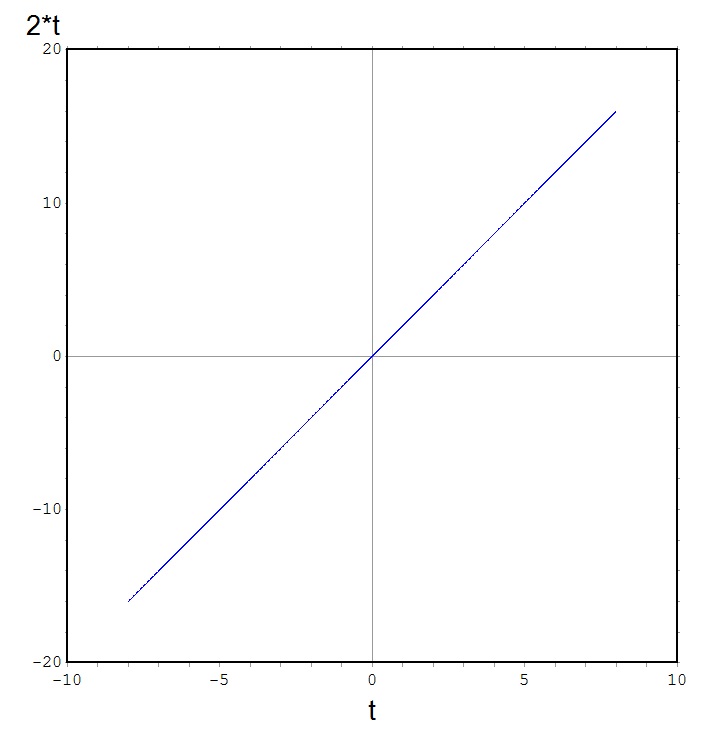Reta imagem da curva plana (t,2t)EXEMPLO

1. F(0)=(1,0)
2. A imagem de F é dada por $$\left\{(x,y) \in \mathbb{R}^2 ; x^2+y^2 = 1\right\}$$
3. Essa função vetorial expressa o movimento de uma partícula P sobre uma cirfunferência de raio 1. Neste caso, a variável t representa o tempo e a função F(t) nos dá a posição da partícula em movimento.

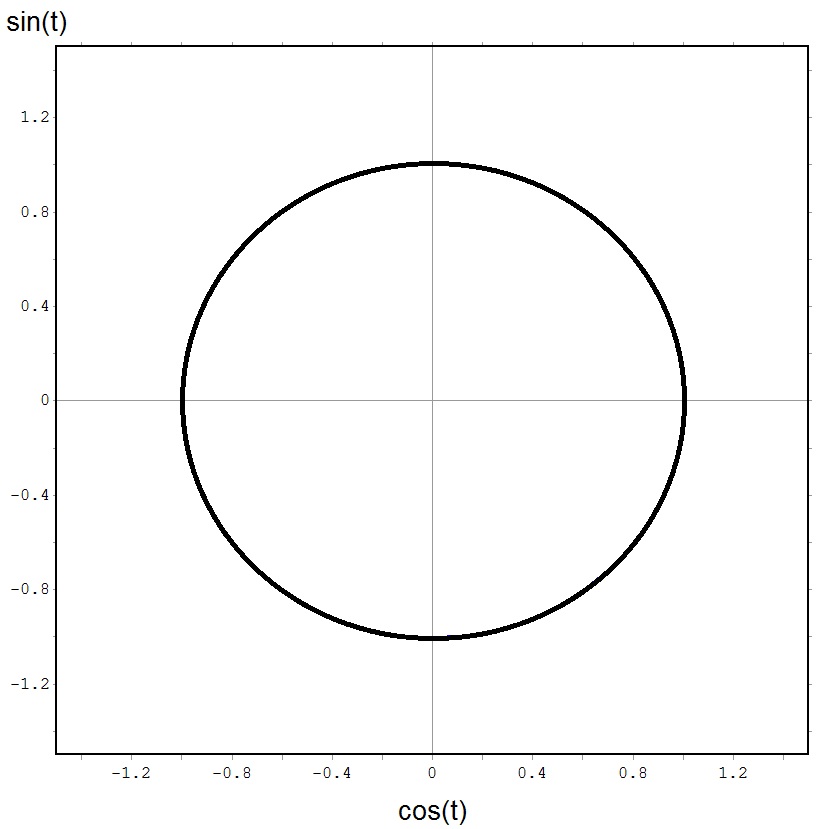Circunferência de centro em (0,0) e raio 1EXEMPLO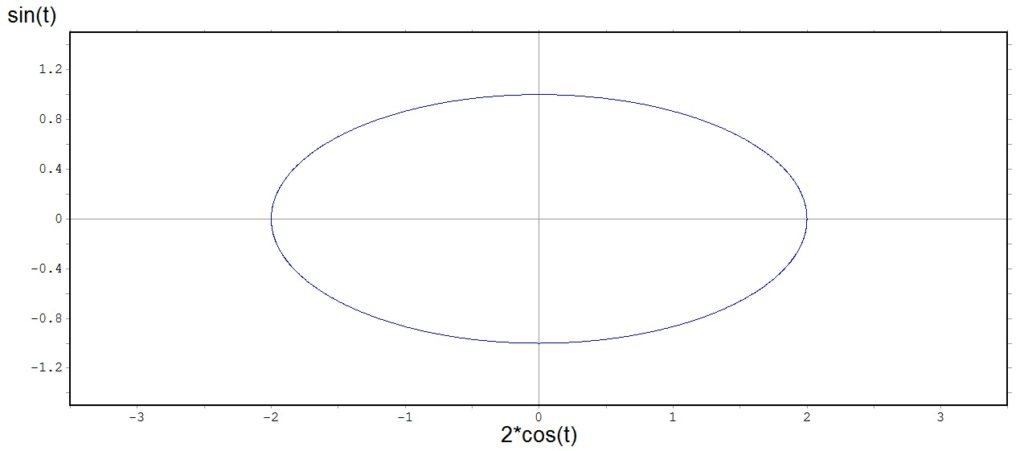Elipse com centro na origem e raio maior igual, sobre o eixo xEXEMPLO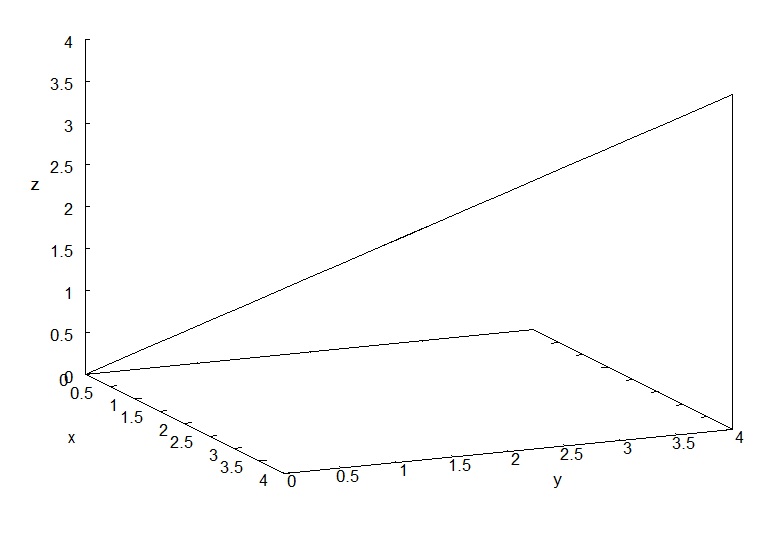Reta imagem da curva espacial F(t) = (t,t,t)EXEMPLO

Hodógrafo

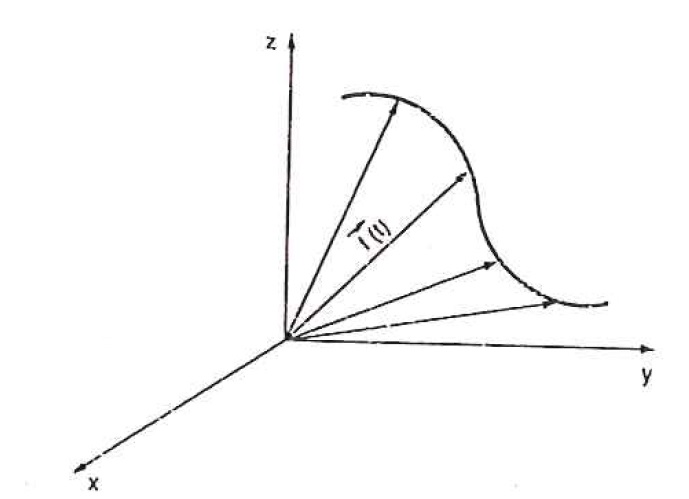Hodógrafo de uma função vetorial de uma variável

Operações Algébricas entre Funções Vetoriais

1. F+G: A \rightarrow \mathbb{R}^n por $$ F+G (t) = F(t) + G(t)$$
2. kF: A \rightarrow \mathbb{R}^n por $$ (kF) (t) = kF(t)$$
3. fF: A \rightarrow \mathbb{R}^n por $$ (fF )(t) = f(t)F(t)$$
4. F.G: A \rightarrow \mathbb{R}^n por $$(F.G)(t)=F(t).G(t)=F_1(t)G_1(t)+F_2(t)G_2(t)+…+F_n(t)G_n(t)$$
5. Sejam F,G: A \subset \mathbb{R} \rightarrow \mathbb{R}^3. (F\wedge G):A \subset \mathbb{R} \rightarrow \mathbb{R}^3é definido por $$
   (F \wedge G)(t) = F(t) \wedge G(t) = \left|
   \begin{array}{ccc}
   i & j & k \\
   F_1(t) & F_2(t) & F_3 (t)\\
   G_1(t) & G_2(t) & G_3(t)
   \end{array} \right|
   $$

EXEMPLO

1. (F+G)(t) = (\cos 3t, \sin 2t, t^2) + (3, t^3, \arctan t) = (\cos 3t + 3, \sin 2t + t^3, t^2+ \arctan t)
2. (3F)(t) = (3 \cos 3t, 3 \sin 2t, 3 t^2)
3. (f.F)(t) = (e^{-2t} \cos 3t, e^{-2t} \sin 2t, e^{-2t} t^2)
4. (G.F)(t) = 3 \cos 3t +t^3 \sin 2t + t^2 \arctan t
5. (F \wedge G)(t) = \left|\begin{array}{ccc}i & j & k \\\cos 3t & \sin 2t & t^2\\3 & t^3 & \arctan t\end{array} \right| = k(t^3 \cos(3t)-3 \sin(2t))-j(\arctan(t) \cos(3t)-3t^2)+i(\arctan(t) \sin(2t)-t^5)

Leia Mais:

• Os Espaços Euclidianos R² e R³ | Cálculo de Várias Variáveis
• Curvas | Reta Tangente, Curvatura, Torção e Fórmulas de Frenet
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Curvas no Espaço | Lista de Exercícios Resolvidos

Assista Nossa Vídeo-Aula no Youtube: