Curvas | A Derivada de Funções Vetoriais

Nesse artigo queremos desenvolver o conceito de derivada para uma função vetorial, ou seja, uma função de uma variável a valores vetoriais, também conhecida como curva.

Uma função de uma variável a valores em \mathbb{R}^n é uma função F:A \rightarrow \mathbb{R}^n, onde A é um subconjunto de \mathbb{R}.

Esta função associa a cada t \in \mathbb{R} um vetor do \mathbb{R}^n.

O conjunto A é o domínio da função F, que consideraremos sempre como um intervalo ou uma união de intervalos, e notado por D_F.

O conjunto $$ImF=\left\{F(t) \in \mathbb{R}^n ; t \in D_F \right\}$$ é a imagem ou a trajetória de F.

Esta função é, por muitas vezes, denominada de função vetorial ou curva.

A Derivada de Funções Vetoriais

Uma função vetorial F: A \in \mathbb{R} \rightarrow \mathbb{R}^né derivável em um ponto t_0se cada uma de suas funções coordenadas for derivável neste ponto.

Neste caso, a derivada de uma função F(t)é definida por $$F'(t)=\frac{dF}{dt}=\left( \frac{dF_1}{dt}, \frac{dF_2}{dt}, …, \frac{dF_n}{dt}\right).$$

Isso foi algo inferido nesse artigo onde desenvolvemos a teoria de limite e continuidade para funções vetoriais.

EXEMPLO

Seja F(t) = \left( \sin{3t}, e^{t^2}, t \right).

Desta forma,

1. \frac{dF}{dt}(t) = \left( 3\cos{3t}, 2t e^{t^2}, 1 \right)
2. \frac{dF}{dt}(0) = \left( 3, 0, 1 \right)

EXEMPLO

A função vetorial r(t) = t^2 i +\arctan{2t}j+e^{-t}k está escrita em sua forma vetorial.

Facilmente podemos ver que

1. r'(t) = 2ti+2\frac{1}{1+4t^2}j-1e^{-t}k
2. r''(0) = 2i - \frac{16t}{\left(1+4t^2\right)^2}j+e^{-t}k

Interpretação Geométrica

Geometricamente, F'\left(t_0 \right)representa a direção tangente à curva F(t)no ponto t_0, desde que F'\left(t_0 \right) \neq 0.

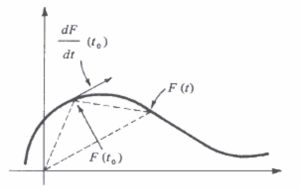
Vetor Tangente à Trajetória de Uma Curva

Seja F:A \rightarrow \mathbb{R}^nderivável em t_0, com F'(t_0) \neq 0.

Dizemos que F'(t_0)é o vetor tangente à trajetória de F, em F(t_0).

A equação da reta tangente à curva no ponto F(t_0)é dada $$X=(x_1, x_2,…,x_n) = F(t_0)+\lambda F'(t_0),\;\;\; \lambda \in \mathbb{R}$$

EXEMPLO

Seja F(t)=\left( \cos{t}, \sin{t} \right), t \in \mathbb{R}.

Determine a equação da reta tangente à trajetória de Fno ponto F\left(\frac{\pi}{4}\right).

Para isso vamos determinar os elementos a serem substituídos na fórmula da equação da reta tangente dada anteriormente:

1. F\left( \frac{\pi}{4} \right)=\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)
2. \frac{dF}{dt}(t)=\left( -\sin{t}, \cos{t} \right) \Rightarrow \frac{dF}{dt}\left(\frac{\pi}{4}\right)=\left( -\sin{\left(\frac{\pi}{4}\right)}, \cos{\left(\frac{\pi}{4}\right)} \right)=\left( -\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)

Logo, a equação da reta tangente é dada por (x,y)=\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) + \lambda \left( -\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right),\;\;\; \lambda \in \mathbb{R}

A Interpretação Física da Derivada de Uma Função Vetorial de Uma Variável

Considere o vetor \vec{f} (t) = (x(t), y(t), z(t) como o vetor posição da partícula com relação a um sistema de coordenadas cartesianas tridimensionais, em relação ao tempo t.

A taxa média de variação de \vec{f} (t) = (x(t), y(t), z(t)) no intervalo \Delta t é dada por $$ \frac{\vec{f} (t + \Delta t) – \vec{f} (t)}{\Delta t} $$ e é chamada de velocidade média da partícula no intervalo de tempo \Delta t.

Aplicando o limite com \Delta t tendendo a zero nessa velocidade média da partícula, encontramos o vetor \vec{v} (t) = \vec{f'} (t), que é a velocidade instantânea da partícula no tempo t, quando o limite que define esta derivada existe.

Quando \vec{v} (t) admite derivada, então \vec{a} (t) = \vec{v'} (t) = \vec{f''} (t) será a aceleração da partícula.

EXEMPLO
Determine o vetor velocidade e o vetor aceleração de uma partícula que se move segundo a lei $$\vec{f} (t) = (cos(2t), sen(2t), 1).$$ Mostre que o vetor posição é perpendicular ao vetor velocidade e que o vetor aceleração também é perpendicular ao vetor velocidade.

De forma simples e direta podemos perceber que $$ \vec{v} (t) = (-2sen(2t), 2cos(2t), 0)\;\;\;e$$ $$\vec{a} (t) = (-4cos(2t), -4sen(2t), 0).$$ Logo, por cálculos simples de produtos escalares podemos perceber que $$\vec{v} (t) . \vec{f} (t)= 0$$ e $$\vec{v} (t) . \vec{a} (t)= 0,$$ mostrando o resultado pedido.

REGRAS DE DERIVAÇÃO

As regras de derivação de funçoes vetoriais são similares às de funções escalares.

Sejam F,G: A \rightarrow \mathbb{R} ^n, f: B \rightarrow \mathbb{R}deriváveis em A.Então,

1. \frac{d }{dt}\left( F(t)+G(t) \right)=\frac{d F}{dt}(t)+\frac{d G}{dt}(t)
2. \frac{d }{dt}\left( F(t).G(t) \right)=\frac{d F}{dt}(t).G(t)+ F(t).\frac{d G}{dt}(t)
3. \frac{d }{dt}\left( f(t).F(t) \right)=\frac{d F}{dt}(t).f(t)+ F(t).\frac{d f}{dt}(t)
4. Se F,G: A \rightarrow \mathbb{R} ^3, então $$\frac{d }{dt}\left( F(t) \wedge G(t) \right)=\frac{d F}{dt}(t)\wedge G(t)+ F(t)\wedge \frac{d G}{dt}(t)$$
5. (A Regra da Cadeia) Se f(B) \subset A, então $$\frac{d }{dt}\left( F(f(t)) \right)=\frac{d F}{dt}(f(t)) \left( \frac{df}{dt} \right)(t)$$

EXEMPLO DA REGRA DA CADEIA

Considere F(t)=\left( \cos{t}, \sin{t} \right), t \in \mathbb{R}e f(t)=2t.

Daí, $$\frac{d }{dt}\left( F(f(t)) \right)=\frac{d }{dt} \left( \cos{2t}, \sin{2t} \right)=2\left( -\sin{2t}, \cos{2t} \right).$$

Leia Mais

• Curvas | Limite e Continuidade de uma Função Vetorial
• Curvas | Reta Tangente, Curvatura, Torção e Fórmulas de Frenet
• Curvas no Espaço | Lista de Exercícios Resolvidos
• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula

Assista Nossa Vídeo Aula: