Conceito Básicos e a diferença entre Estatística Descritiva e Inferência!

No mundo de hoje lidamos com uma enorme quantidade de informação, seja de forma bruta (a lista completa de municípios do Brasil com suas populações), seja de modo resumido (gráfico ou tabelas).

A estatística desempenha um papel importante em quase todas as áreas da pesquisa humana.

Encontramos aplicações desta área da matemática na agricultura, biologia, química, comércio, economia,
educação, eletrônica, medicina, ciências políticas e engenharia.

O interesse da estatística é voltado aos métodos científicos para coleta, organização, resumo e apresentação de análises de dados, bem como na obtenção de conclusões válidas e na tomada de decisões razoáveis baseadas em tais análises.

Hoje em dia, o termo estatística é usado para designar os próprios dados ou números deles derivados (médias, modas, medianas, etc.).

Assim, quando falamos em estatística de acidentes ou de desempregos estamos nos referindo a estes dados.

A DIFERENÇA ENTRE ESTATÍSTICA DESCRITIVA E INFERÊNCIA

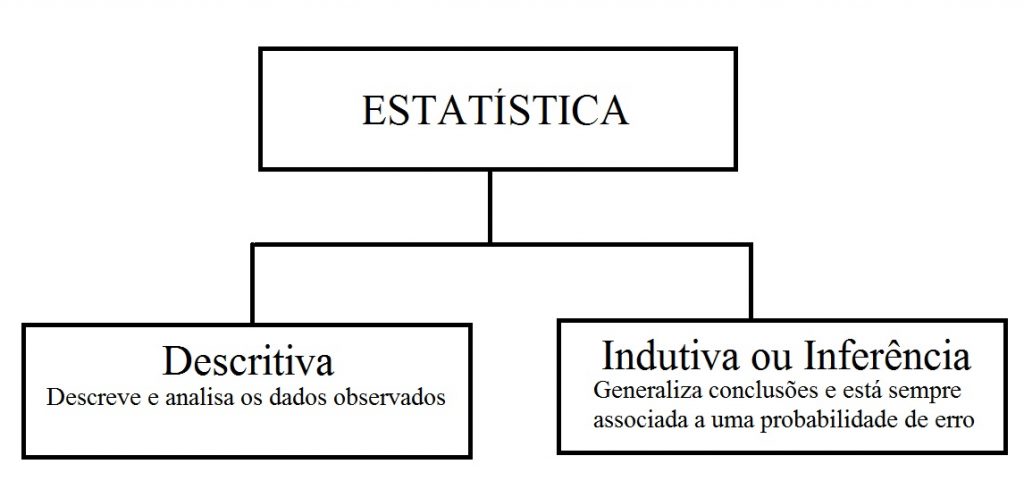
Dividimos a estatística em dois grupos:

1. estatística descritiva: que descreve e analisa um certo grupo sem tirar quaisquer conclusões ou inferências sobre um grupo maior; e
2.  estatística indutiva ou inferência: que apresenta conclusão em relação a um grupo maior com base nos dados de um grupo menor, porém esta análise está associada a uma probabilidade de erro conhecido por grau de incerteza.

CONCEITOS BÁSICOS DA ESTATÍSTICA

Temos, agora, a necessidade de definir alguns termos que serão utilizados em larga escala em estudos estatísticos:

1. População ou Universo: Conjunto de elementos que tem em comum uma característica de estudo. Por exemplo, os estudantes de uma faculdade, a produção diária de uma fábrica.

A população é dividida em duas classes:

1. Finita: possui um número finito de indivíduos. Exemplo: Os alunos de uma sala de aula;
2. Infinita: O número de observações é infinito ou não-mensurável. Exemplo: a população de peixes no oceano Atlântico.

2. Amostra: Conjunto de elementos retirados da população. É interessante observar que a amostra é sempre finita e quanto maior o número de indivíduos na amostra mais significativo é o estudo.

3. Parâmetro: é uma característica numérica estabelecida para toda a população.

4. Estimador: é uma característica numérica estabelecida para uma amostra.

5. Dado Estatístico: é sempre um número real que pode ser:

1. Primitivo ou Bruto: sem transformação matemática;
2. Secundário ou Elaborado: Sofreu transformação matemática.

São exemplos de dados estatísticos a porcentagem, a média.

6. Variáveis: Uma variável é um símbolo, como x,y,H,X,Y,B que pode assumir qualquer um de um conjunto de valores que lhe são atribuídos. As variáveis são divididas em duas classes:

1. Variáveis Contínuas: são aquelas que podem assumir qualquer valor entre dois dados. Por exemplo, a altura H de um indivíduo que pode ser de 1,65 m, 1,662 m ou 1,772 m, conforme a precisão medida
   da variável.
2. Variáveis Discretas: são aquelas que só podem assumir valores representados por números inteiros. Como o número N de crianças em uma família que pode assumir qualquer valor entre {0,1,2,3,4,5…} mas não podem ser 2,5; 0,5 ou 3,2.

Muitas vezes é conveniente estender o conceito de variável a entidades não-numéricas. Por exemplo, o sexo S é uma variável que pode assumir dois valores M (masculino) e F (feminino).

LEIA MAIS:

• Uma Breve História da Estatística!
• Estatística Descritiva | Elaborando um Estudo Estatístico
• Gráficos | Da Análise Estatística ao Mercado de Ações
• Estatística | Distribuição de Frequências e Histograma
• Ajuste de Dados – Como fazer arredondamento de números?