Campos radiais vetoriais são campos da forma \vec{F}=f(r) \hat{r}, isto é campos vetoriais cujo módulo depende apenas da distância até a origem, isto é, de $$r=\|\vec{r}\|=\sqrt{x^2+y^2+z^2}$$ e cuja direção é sempre paralela ao vetor posição, \vec{r}. Neste artigo queremos trabalhar com o Campo Radial de Quadrado Inverso.

Na ciência, uma lei muito importante é do do inverso do quadrado, que é qualquer lei científica que afirma que uma quantidade física especificada é inversamente proporcional ao quadrado da distância da fonte dessa quantidade física. A causa fundamental para isso pode ser entendida como diluição geométrica correspondente à radiação de fonte pontual no espaço tridimensional.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
A divergência de um campo vetorial que é a resultante de campos de lei inversa do quadrado radial com respeito a uma ou mais fontes é em toda parte proporcional à força das fontes locais e, portanto, zero fontes externas. A lei da gravitação universal de Newton segue uma lei do inverso do quadrado, assim como os efeitos dos fenômenos elétricos, de luz, de som e de radiação.
O Campo Radial de Quadrado Inverso
Um campo vetorial é uma função vetorial de várias variáveis onde o domínio e a imagem estão no mesmo espaço espaço euclidiano. Seja A um subconjunto do \mathbb{R}^n e \vec{F} uma transformação de A em \mathbb{R}^n. Se para cada ponto de A o associarmos ao vetor \vec{F} iremos nos referir a \vec{F} como um campo vetorial. Os termos aplicação e transformação são sinônimos de função e várias vezes são utilizadas para diferenciar as funções vetoriais de várias variáveis das demais.
Seja o campo de posição P(x,y,z) . Definimos o seguinte campo: $$ \vec{F} (x,y,z) = \frac{k}{\| P(x,y,z) \| ^3 } P(x,y,z) ,$$ sendo k \in \mathbb{R} . Se k < 0 então este campo vetorial apontará para a origem do sistema de coordenadas.
Este campo é denominado campo radial de quadrado inverso e não está definido, obviamente, na origem do sistema de coordenadas.
Observe que quanto mais afastado da origem está P(x,y,z) menor é a norma do campo \vec{F} (x,y,z) .
Além disso, podemos observar por $$ \| \vec{F} (x,y,z) \|= \frac{|k|}{\| P(x,y,z) \| ^2 }$$ que a norma do campo \vec{F} (x,y,z) é inversamente proporcional ao quadrado da distância da origem ao ponto (x,y,z).
São exemplos de campos radiais de quadrado inverso: 1) a força exercida sobre una partícula de massa m descrita nas condições da lei da gravitação universal de Newton; e 2) o campo elétrico gerado por uma partícula carregada e regido pela lei de Coulomb.
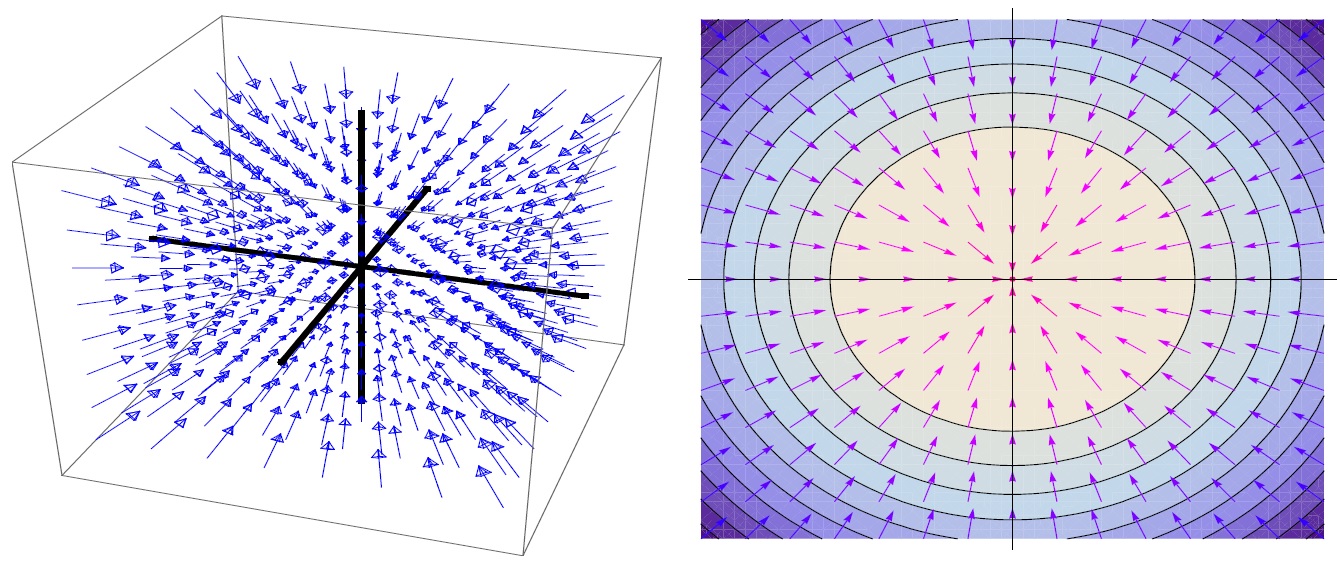 Campo Radial de Quadrado Inverso com k = −1 e sua projeção no plano.
Campo Radial de Quadrado Inverso com k = −1 e sua projeção no plano.
O Campo Radial de Quadrado Inverso é Conservativo
Um campo vetorial \vec{F}(x,y): \Omega \subset \mathbb{R}^n \rightarrow \mathbb{R}^n denomina-se conservativo se existe um campo escalar diferenciável \varphi: \Omega \rightarrow \mathbb{R} tal que
\begin{equation}
\nabla \varphi = \vec{F}\;\;\;em\;\;\;\Omega. \label{conservativo}
\end{equation}
Portanto, um campo vetorial é conservativo se é um campo gradiente.
Uma função \varphi que satisfaz essa igualdade denomina-se função potencial de \vec{F}.
Seja o campo de posição P(x,y,z) . Definimos o seguinte campo: $$ \vec{F} (x,y,z) = \frac{k}{\| P(x,y,z) \| ^3 } P(x,y,z) ,$$ sendo k \in \mathbb{R} . Se k < 0 então este campo vetorial apontará para a origem do sistema de coordenadas.
Este campo é denominado campo radial de quadrado inverso e não está definido, obviamente, na origem do sistema de coordenadas.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Este campo é conservativo e suas coordenadas são dadas por $$F_1 (x,y,z) = \frac{ k x}{(x^2 + y^2 + z^2) ^{3/2}} $$ $$F_2 (x,y,z) = \frac{ k y}{(x^2 + y^2 + z^2) ^{3/2}} $$ $$F_3 (x,y,z) = \frac{ k z}{(x^2 + y^2 + z^2) ^{3/2}} $$
Então $$ M(x,y,z) = \int{ \frac{ k x}{(x^2 + y^2 + z^2) ^{3/2}} dx} = – \frac{ k x}{\sqrt{x^2 + y^2 + z^2}}.$$ Agora, facilmente podemos calcular e encontrar $$ N(x,y,z) = L(x,y,z) = 0 .$$ Portanto, o potencial é $$ f(x,y,z) = – \frac{ k x}{\sqrt{x^2 + y^2 + z^2}} + c .$$
As Curvas de Fluxo (ou Curvas Integrais) do Campo Radial de Quadrado Inverso
Se \vec{F} é um campo vetorial contínuo, \gamma é uma curva do fluxo de \vec{F} se $$\gamma ‘ (t) = \vec{F}( \gamma (t)).$$
As curvas que formam o fluxo do campo são também chamadas de curvas integrais do campo, pois se \vec{F}(x,y,z) = F_1(x,y,z) \vec{ i } + F_2(x,y,z) \vec{ j } + F_3(x,y,z) \vec{ k } representa a velocidade das partículas num fluido, o movimento do fluido é completamente determinado pelo sistema $$\frac{dx}{dt} = F_1 \left( x(t), y(t), z(t) \right) $$ $$\frac{dy}{dt} = F_2 \left( x(t), y(t), z(t) \right) $$ $$\frac{dz}{dt} = F_3 \left( x(t), y(t), z(t) \right) ;$$ o que nos leva a associar o campo \vec{F} a um sistema de equações diferenciais ordinárias, cuja solução é o fluxo \gamma (t) = \left( x(t), y(t), z(t) \right) de \vec{F}.
O fluxo do campo quadrado inverso é dado por $$ \gamma (t) = \sqrt[3]{k t} \vec{u} $$ onde \vec{u} \in \mathbb{R}^3 é um vetor unitário fixo.
Leia Mais:
- Campos Vetoriais | Definição e Primeiros Exemplos
- O que são Campos Conservativos? Como Calcular o Potencial?
- Campo Vetorial | O que são as Curvas de Fluxo ou Curvas Integrais?
- O Divergente de um Campo Vetorial | Definição e Interpretação
Referências Bibliográficas:
- GUIDORIZZI, H.L. Um curso de cálculo: Vol 1, 2,3 e 4. Rio de Janeiro: LTC, 2001.
- KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.
- STEWART, J. Cálculo, vol 1 e 2. São Paulo: Editora Pioneira – Thomson Learning, 2001.


