Calculando Integrais de Linha de Forma Rápida e Fácil

Aprenda os truques para resolver problemas desafiadores de integrais de linha de forma rápida e fácil!

Resolver problemas de integrais de linha pode ser complicado e demorado. Mas dominar as técnicas e truques usados por matemáticos experientes pode tornar essa tarefa muito mais simples. Neste guia, forneceremos todas as ferramentas e dicas necessárias para calcular integrais de linha de maneira rápida e fácil.

Compreendendo os conceitos básicos de integrais de linha.

Antes de fazer qualquer cálculo, é importante entender os fundamentos das integrais de linha. Integrais de linha envolvem a integração de funções sobre um caminho fechado ou curva no espaço. A integral de linha de uma função consiste em duas partes: um campo vetorial e um vetor que parametriza a curva. Entender esses componentes é crucial para descobrir como resolver problemas de integrais de linha com facilidade.

INTEGRAL DE LINHA DE PRIMEIRA ESPÉCIE

Nosso intuito é calcular a integral de uma função f(x,y,z) ao longo da curva C de A até B.

Esta integral sera denotada por $$\int\limits_{C}{f(x,y,z)}ds$$ onde s é o comprimento de arco da curva C que é denominada caminho de integração.

Imediatamente temos que

\begin{eqnarray*}
\int\limits_{C}{f(x,y,z)}ds & = & \int\limits_{a}^{b}{f(x(s),y(s),z(s))}ds\\
& = & \int\limits_{t_1}^{t_2}{f(x(t),y(t),z(t))}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2+ \left(\dfrac{dz}{dt}\right)^2}dt\\
\end{eqnarray*}

Esta integral é denominada integral de linha de primeira espécie de f sobre C.

Observe que para definir a integral de linha acima não é necessário que a função f esteja definida em ponto fora de C. Em particular, se \lambda =  \lambda (s) for uma função contínua do arco s , podemos definir sua integral sobre  C.

INTEGRAL DE LINHA DE SEGUNDA ESPÉCIE

Vamos considerar agora L=L(x,y,z), M=M(x,y,z) e N=N(x,y,z) funções definidas e contínuas numa região R de espaço de modo que $$\vec{F}(x,y,z) = L(x,y,z)i+M(x,y,z)j+N(x,y,z)k$$ seja um campo vetorial definido no aberto R e seja C um arco regular, todo contido em R com representação paramétrica $$P(t) = x(t) i + y(t) j +z(t) k\;\;\;\;a\leq t \leq b$$ que descreve um movimento em R.

Vamos definir a integral de linha de \vec{F}, ao longo do arco C, como sendo $$\int\limits_{C}{Ldx+Mdy+Ndz} = \int\limits_{C}{\vec{F}(P(t)).dP} $$ onde F(P) = (L(P(t)),M(P(t)), N(P(t))) e dP = (x'(t)dt, y'(t)dt, z'(t)dt) = P'(t)dt.

O Teorema de Green

Um dos teoremas mais úteis para simplificar questões de integrais de linha é o Teorema de Stokes, que afirma que a integral de linha de um campo vetorial ao longo de uma curva fechada é igual à integral de superfície de sua rotacional sobre qualquer superfície limitada por essa curva. Isso significa que integrais de linha complexas podem ser reduzidas a integrais de superfície mais simples, tornando-as mais fáceis de resolver. Para aplicar o Teorema de Stokes, você precisa entender como integrar um cacho sobre uma superfície e ser capaz de reconhecer quando ele deve ser usado.

Teorema de Green no Plano

Seja R uma região fechada e limitada no plano xy cuja fronteira consiste de uma quantidade finita de curvas regulares. Sejam f(x,y) e g(x,y) funções contínuas e cujas derivadas parciais \dfrac{\partial f}{\partial y} e \dfrac{\partial g}{\partial x} também são contínuas em algum domínio R. Então: $$\int\limits_{R} \int \left( \dfrac{\partial g}{\partial x} – \dfrac{\partial f}{\partial y} \right) dx dy= \int\limits_{C}\left( fdx +gdy \right).$$

Resolvendo Integrais de Linha – Exercícios Resolvidos

1) Calcule \int_{C}{\left( x^2 + 2 y^2 \right)ds}, onde C(t) = \left(cos(t), sen(t) \right); 0 \leq t \leq 2 \pi;

SOLUÇÃO: $$ \int_{C}{\left( x^2 + 2 y^2 \right)ds} = \int\limits_{0}^{2 \pi}{(cos^2 t + 2 sen^2(t))\| (-sen(t), cos(t))\| dt} = \\ =\int\limits_{0}^{2 \pi}{(cos^2 t + 2 sen^2(t))dt} = \int\limits_{0}^{2 \pi}{[1+ sen^2(t)] dt} – 3 \pi.$$

2) Calcule a integral \int_{C}{\vec{f}\cdot \vec{dr}} onde:

a) \vec{f}(x,y) = (x,y) e C(t) = \left(t, t^2 \right), t\in [-1,1];

SOLUÇÃO: Observando que $$ \vec{f}(C(t)) = \vec{f}(t,t^2) = t \vec{i} + t^3 \vec{j}$$ e que $$C'(t) = (1, 2t)$$ podemos calcular $$\int\limits_{C}{\vec{f}\cdot \vec{dr}} = \int\limits_{-1}^{1}{\vec{f}(C(t))\cdot C'(t) dt} = \int\limits_{-1}^{1}{(t + 2 t^3)dt} = 0$$

b) \vec{f}(x,y) = \dfrac{-y}{x^2 +y^2} \vec{i} + \dfrac{x}{x^2 +y^2} \vec{j} e C(t) = \left(cos(t), sen(t) \right); 0 \leq t \leq 2 \pi;

SOLUÇÃO: $$\int\limits_{C}{\vec{f}\cdot \vec{dr}} = \int\limits_{0}^{2 \pi}{\left[ \frac{-y}{x^2 +y^2} \vec{i} + \frac{x}{x^2 +y^2} \vec{j} \right] \cdot (-sen(t) , cos(t) ) dt } = \int\limits_{0}^{2 \pi}{dt} = 2 \pi$$

3) Calcule a integral \int_{C}{Ldx + Mdy + Ndz} onde:

a) \int_{C}{xdx + (x^2 + y +z)dy + (xyz)dz} onde C(t) = \left(t, 2t, 1 \right); t \in [0,1].

SOLUÇÃO: De x = t , y =2 t e z = 1 , segue \dfrac{dx}{dt} = 1 , \dfrac{dy}{dt} = 2 e \dfrac{dz}{dt} = 0 . Temos: $$ \int_{C}{xdx + (x^2 + y +z)dy + (xyz)dz} = \int\limits_{0}^{1}{\left[ t \frac{dx}{dt} + (t^2+2t+1) \frac{dy}{dt} +2t^2 \frac{dz}{dt} \right] dt} = \\ = \int\limits_{0}^{1}{\left[ t+2(t^2+2t+1) \right]dt} = \frac{31}{6}. $$

b) \int_{C}{-ydx + xdy} onde C(t) é a curva fechada cuja imagem é a elipse \dfrac{x^2}{4} + \dfrac{y^2}{9} = 1.

SOLUÇÃO: Uma parametrização que atende as condições dadas é $$ x(t) = 2 cos(t); \qquad y(t) = 3 sen(t); \qquad 0 \leq t \leq 2 \pi .$$ Temos, então, que $$\int_{C}{-ydx + xdy} = \int\limits_{0}^{2 \pi}{\left[ -3sen(t) \frac{dx}{dt} + 2 cos(t) \frac{dy}{dt} \right]dt} = \\ = \int\limits_{0}^{2 \pi}{\left[ 6 sen^2 (t)+ 6 cos^2 (t) \right]dt} = 12 \pi.$$

c) \int_{\gamma }{xdx + xydy} onde \gamma (t) = (t , |t|), t \in [-1,1]

SOLUÇÃO: $$ \int_{\gamma}{xdx + xydy} = \int_{\gamma _1}{xdx + xydy}+ \int_{\gamma _2}{xdx + xydy}$$ onde $$\gamma _1: x(t) = t, \;\;\; y(t) = -t; \;\;\; -1 \leq t \leq 0 $$ e $$ \gamma _2: x(t) = t, \;\;\; y(t) = t ; \;\;\; 0 \leq t \leq 1.$$

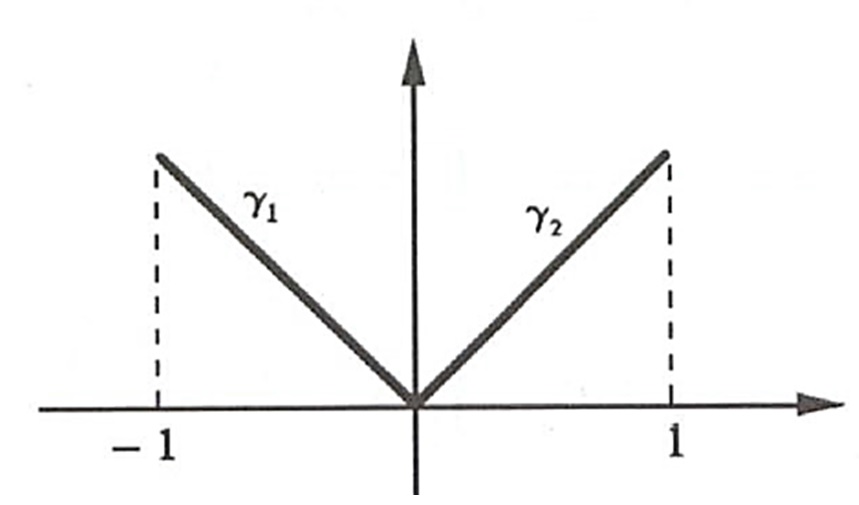
Logo, $$ \int_{\gamma _1}{xdx + xydy} = \int\limits_{-1}^{0}{(t+t^2)dt} = – \frac{1}{6} $$ e $$ \int_{\gamma _2}{xdx + xydy} = \int\limits_{0}^{1}{(t+t^2)dt} = \frac{5}{6} .$$ Portanto, $$ \int_{\gamma}{xdx + xydy} = \int_{\gamma _1}{xdx + xydy}+ \int_{\gamma _2}{xdx + xydy} = \frac{2}{3}.$$

d) \int_{\gamma}{xdx + ydy} onde \gamma (t) é a curva cuja imagem é poligonal de vértices (0,0), (2,0) e (2,1), orientada de (0,0) para (2,1).

SOLUÇÃO: Uma parametrização para \gamma (t) é $$\gamma (t) = (t,0), \text{ se } 0 \leq t \leq 2; \qquad \text{e} \qquad \gamma (t) = (2,t-2), \text{ se } 2 \leq t \leq 3.$$

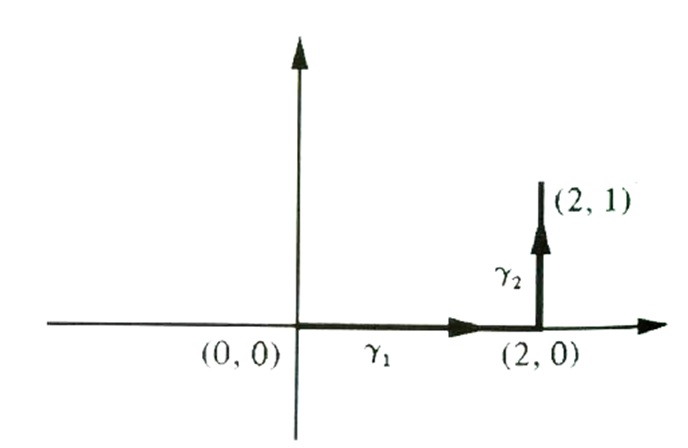
Temos: $$ \int_{\gamma}{xdx + ydy} = \int_{\gamma _1}{xdx + ydy}+ \int_{\gamma _2}{xdx + ydy}$$ onde $$\gamma _1: x(t) = t, \;\;\; y(t) = 0; \;\;\; 0 \leq t \leq 2 $$ e $$ \gamma _2: x(t) = 2, \;\;\; y(t) = t-2 ; \;\;\; 2 \leq t \leq 3.$$

Logo, $$ \int_{\gamma _1}{xdx + ydy} = \int\limits_{0}^{2}{tdt} = 2 $$ e $$ \int_{\gamma _2}{xdx + ydy} = \int\limits_{2}^{3}{(t-2)dt} = \frac{1}{2} .$$ Portanto, $$ \int_{\gamma}{xdx + ydy} = \int_{\gamma _1}{xdx + ydy}+ \int_{\gamma _2}{xdx + ydy} = \frac{5}{2}.$$

e) \int_{C}{-ydx + xdy} onde \gamma (t) é o triângulo de vértices (0,0), (1,0) e (1,1), orientada no sentido anti-horário.

SOLUÇÃO: $$ \int_{\gamma}{-ydx + xdy} = \int_{\gamma _1}{-ydx + xdy}+ \int_{\gamma _2}{-ydx + xdy}+ \int_{\gamma _3}{-ydx + xdy}$$ onde $$\gamma _1: x(t) = t, \;\;\; y(t) = 0; \;\;\; 0 \leq t \leq 1, $$ $$ \gamma _2: x(t) = 1, \;\;\; y(t) = t ; \;\;\; 0 \leq t \leq 1 ,$$ e $$ \gamma _3: x(t) = 1-t, \;\;\; y(t) = 1- t ; \;\;\; 0 \leq t \leq 1.$$

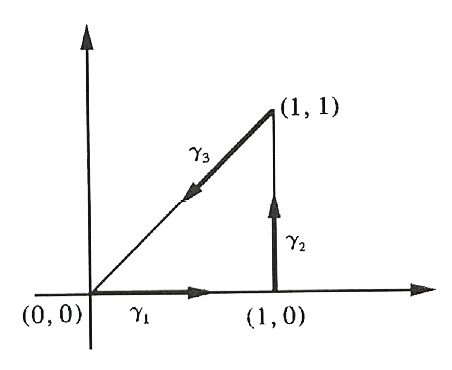
Temos que $$ \int_{\gamma _1}{-ydx + xdy} = 0 $$ $$\int_{\gamma _2}{-ydx + xdy} = \int\limits_{0}^{1}{dt} = 1$$ $$ \int_{\gamma _3}{-ydx + xdy} = 0.$$ Portanto, $$ \int_{\gamma}{-ydx + xdy} = \int_{\gamma _1}{-ydx + xdy}+ \int_{\gamma _2}{-ydx + xdy}+ \int_{\gamma _3}{-ydx + xdy} = 1.$$

4) Usando o Teorema de Green no plano calcule: $$\int_{C}{(x^4 – y^3)dx + (x^3 + y^5) dy}, \qquad \text{onde }C(t) = \left(cos(t), sen(t) \right); \qquad 0 \leq t \leq 2 \pi.$$

SOLUÇÃO:  P(x,y) = x^4 - y^3 e Q(x,y) = x^3 + y^5 são de classe C^1 em \mathbb{R} ^2 . A imagem de \gamma é a fronteira do círculo dado K dado por x^2 + y^2 \leq 1 , que esta contido em \mathbb{R} ^2 . Pelo teorema de Green $$ \int_{C}{(x^4 – y^3)dx + (x^3 + y^5) dy} = \iint\limits_{K}{\frac{\partial Q}{\partial x} – \frac{\partial P}{\partial y}dxdy}.$$ Como $$ \frac{\partial Q}{\partial x} – \frac{\partial P}{\partial y} = 3x^2+3y^2 $$ resulta que $$\int_{C}{(x^4 – y^3)dx + (x^3 + y^5) dy} = 3 \iint\limits_{K}{\left( x^2 + y^2 \right) dxdy} = \frac{3 \pi}{2}.$$

Referências Bibliográficas:

1. GUIDORIZZI, H.L. Um curso de cálculo: Vol 1, 2,3 e 4. Rio de Janeiro: LTC, 2001.
2. LEITHOLD, L. O cálculo com geometria analítica, vol 1 e 2. São Paulo: Editora Harbra, 1994.
3. SWOKOWSKI, E.W. Cálculo com geometria analítica, vol 1 e 2. São Paulo: Makron Books, 1994.
4. KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.
5. BATSCHELET, E. Introdução à Matemática para Biocientistas. São Paulo: Editora da USP, 1978.
6. ÁVILA, Geraldo S. S. Cálculo 3 – Funções de Várias Variáveis. 5ª Edição. Rio de Janeiro: LTC, 1995.

Leia Mais:

• Integral de Linha de 1ª e 2ª Espécies | Teorema de Green no Plano
• Integral de Linha de 1ª Espécie | 1ª Lista de Exercícios Resolvidos
• Integral de Linha de Campos Vetoriais | 1ª Lista de Exercícios Resolvidos
• O Teorema de Green No Plano | Lista de Exercícios Resolvidos.