O DIVERGENTE de um campo vetorial mede a densidade da mudança na força do campo vetorial. Em outras palavras, a divergência mede a taxa instantânea de mudança na força do campo vetorial ao longo da direção do fluxo.
Neste artigo queremos definir o divergente de um campo vetorial. Campos vetoriais são usados para modelar campos de força (gravidade, campos elétricos e magnéticos), fluxo de fluido, etc.
| Mais abaixo, neste artigo, temos uma vídeo-aula e uma lista com vários exercícios resolvidos sobre o DIVERGENTE de um campo vetorial. |
Seja A um subconjunto do \mathbb{R}^n e \vec{F} uma transformação de A em \mathbb{R}^n. Se para cada ponto de A o associarmos ao vetor \vec{F} iremos nos referir a \vec{F} como um campo vetorial.
No espaço \mathbb{R}^3, considere P(x,y,z) um ponto de um conjunto de pontos do espaço. Se para cada ponto P deste conjunto associarmos um vetor \vec{F}(P) = \vec{F}(x,y,z), então obtemos um campo vetorial para estes pontos e \vec{F}(x,y,z) é denominada função vetorial.
Em coordenadas cartesianas, $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ onde i = (1,0,0), j = (0,1,0) e k = (0,0,1) e F_i : \mathbb{R}^3 \rightarrow \mathbb{R}
O Divergente de Um Campo Vetorial
Seja $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ o campo vetorial definido em um aberto A do \mathbb{R}^3 e suponha que F_i admita derivadas parciais para i=1,2,3.
O divergente de \vec{F}, que se denota por div(\vec{F}), é o campo vetorial definido em A e dado por $$div\left( \vec{F} \right) = \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} = \nabla . \vec{F}$$ onde \nabla é o vetor gradiente.
Se imaginarmos um campo vetorial como um campo de velocidades de um gás ou de um fluido, então a divergência do campo está relacionada cam a expansão ou a contração do volume do volume do gás pelo fluxo do campo.
EXEMPLO
Considere \vec{F}(x,y,z) = (x^2+z)i-y^2 j + (2x+3y+z^2)k. Vamos calcular o divergente deste campo vetorial.
$$div\left( \vec{F} \right)(x,y,z) = \frac{\partial}{\partial x}(x^2+z) + \frac{\partial}{\partial y}(-y^2) + \frac{\partial}{\partial z}(2x+3y+z^2) = 2x – 2y + 2z.$$
Campo Incompressível
Se div{\vec{F}}=0 então dizemos que o campo vetorial \vec{F} é dito incompressível.
OBSERVAÇÃO:
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
EXEMPLO
Se F(x,y) = (y,-x), então $$div\left( \vec{F} \right)(x,y) = \frac{\partial}{\partial x}(y) + \frac{\partial}{\partial y}(-x) = 0. $$
Este campo vetorial é dito incompressível e tem representação dada na figura abaixo.
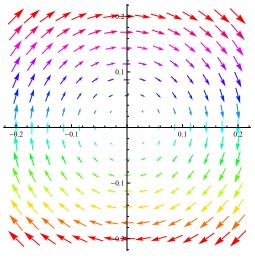 Fluxo Incompressível
Fluxo Incompressível
Listas de Exercícios Resolvidos
Leia Mais:
- Campos Vetoriais Conservativos e Potencial
- Campo Vetorial | O que são as Curvas de Fluxo ou Curvas Integrais?
- O Rotacional de um Campo Vetorial | Definição e Interpretação Geométrica
- O Divergente de um Campo Vetorial | Definição e Interpretação
- Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano

