O Que São Funções Periódicas? Definição e Exemplos.

Uma função f:\mathbb{R} \rightarrow \mathbb{R} é chamada de função periódica de período T se $$f(x+T) = f(x)$$ para todo x.

O menos valor de T > 0 é chamado período mínimo, ou simplesmente período, de f(x).

Por exemplo, a função f(x) = sen(x) tem períodos iguais a 2 \pi , 4 \pi , 6 \pi , .... , pois sen(x) = sen(x + 2 \pi) = sen(x + 4 \pi) = sen(x + 6 \pi) =... , . Todavia, 2 \pi é o período mínimo, ou período da função seno.

Já para um função constante, o período é qualquer número positivo.

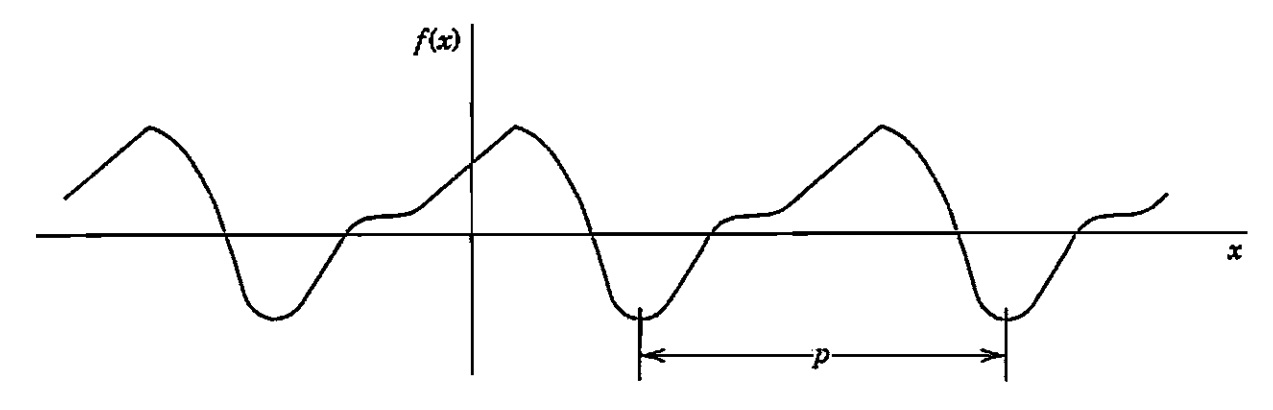
O gráfico de uma função periódica é obtido pela repetição periódica do seu gráfico em qualquer intervalo de tamanho T.

EXEMPLO 1

• As funções \sin{x} e \cos{x} são periódicas e com período igual a 2 \pi.
• A função \tan{x} é periódica e com período igual a \pi.

EXEMPLO 2

Determine o período da função \sin{(nx)}.

Da periodicidade da função seno podemos concluir que \sin{(nx)} é periódica com período T.

Daí

$$\sin{\left( n(x+T) \right)} = \sin{(nx)}$$ $$\Updownarrow$$ $$\sin{(nx)} \cos{(nT)} + \sin{(nT)} \cos{(nx)} = \sin{(nx)}.$$

Como o período da função seno é 2\pi, ficamos motivamos a tomar x=\frac{2\pi}{n} na igualdade acima.

Logo, $$\sin{(2\pi)} \cos{(nT)} + \sin{(nT)} \cos{(2\pi x)} = \sin{(2\pi)}$$ $$\Updownarrow$$ $$\sin{(nT)} = \sin{(2\pi)}$$ $$\Updownarrow$$ $$nT =2\pi \Leftrightarrow T = \frac{2 \pi}{n}.$$

É interessante ficar atento ao fato de que \sin{(2k\pi)} = \sin{(2\pi)}, k \in \mathbb{Z}.

No exemplo acima, a conclusão $$\sin{(nT)} = \sin{(2\pi)} \Leftrightarrow nT = 2\pi$$ é tomada, pois queremos encontrar o menor valor de T>0 tal que \sin{(nT)} = \sin{(2\pi)}.

Assim, nT = 2k\pi, onde k não pode ser zero, pois caso contrário, T=0. Por consequência, k=1.

EXEMPLO 3

As funções \cos{\left(\frac{n \pi}{L} x\right)} e \sin{\left(\frac{n \pi}{L} x\right)} são periódicas e com período \frac{2 L}{n}.

Vamos verificar estar afirmação para a função \cos{\left(\frac{n \pi}{L} x\right)}, sendo a verificação da afirmação para a função \sin{\left(\frac{n \pi}{L} x\right)} deixada como exercício.

Como \cos{x} é periódica, por consequência \cos{\left(\frac{n \pi}{L} x\right)} também o será.

Seja T este período.

Assim, $$\cos{\left(\frac{n \pi}{L} (x+T)\right)} = \cos{\left(\frac{n \pi}{L} x\right)}$$ $$\Updownarrow$$ $$\cos{\left(\frac{n \pi}{L} x\right)}\cos{\left(\frac{n \pi}{L} T\right)} – \sin{\left(\frac{n \pi}{L} x\right)}\sin{\left(\frac{n \pi}{L} T\right)} = \cos{\left(\frac{n \pi}{L} x\right)}, \forall x \in \mathbb{R}$$

Sem perda de generalidade, tome x = \frac{2L}{n}. Assim,

$$\cos{\left(2\pi \right)}\cos{\left(\frac{n \pi}{L} T\right)} – \sin{\left(2\pi \right)}\sin{\left(\frac{n \pi}{L} T\right)} = \cos{\left(2\pi\right)}$$ $$\Updownarrow$$
$$\cos{ \left(\frac{n \pi}{L} T\right) } = \cos{\left(2\pi \right)} \Leftrightarrow \frac{n \pi}{L} T = 2 \pi \Leftrightarrow T = \frac{2L}{n}.$$

Note que tomamos x = \frac{2L}{n}$ para que \frac{n \pi}{L} T = 2 \pi.

Porém, obteríamos o mesmo resultado se tomássemos x=\frac{L}{n} ou x= \frac{n}{2L}.

Se tomarmos x=\frac{L}{n} no momento em que consideramos x = \frac{2L}{n} no exemplo anterior, então chegaríamos em

$$\cos{\left(\pi \right)}\cos{\left(\frac{n \pi}{L} T\right)} – \sin{\left(\pi \right)}\sin{\left(\frac{n \pi}{L} T\right)} = \cos{\left(\pi\right)}$$ $$\Updownarrow$$
$$-\cos{\left(\frac{n \pi}{L} T\right)} = \cos{\left(\pi\right)} \Leftrightarrow \cos{\left(\frac{n \pi}{L} T\right)} = -\cos{\left(\pi\right)}.$$

Porém, \cos{(x)} satisfaz a seguinte propriedade - \cos{(x)} = \cos{(x+\pi)}, ou seja, -\cos{\left(\pi\right)}=\cos{2\pi}.

Daí, $$\frac{n \pi}{L} T = 2 \pi \Leftrightarrow T = \frac{2L}{n}.$$

Por outro lado, se tomarmos x=\frac{L}{2n} no momento em que consideramos x = \frac{2L}{n} no exemplo anterior, então chegaríamos em
$$\cos{\left(\frac{\pi}{2} \right)}\cos{\left(\frac{n \pi}{L} T\right)} – \sin{\left(\frac{\pi}{2} \right)}\sin{\left(\frac{n \pi}{L} T\right)} = \cos{\left(\frac{\pi}{2}\right)}$$ $$\Updownarrow$$
$$- \sin{\left(\frac{n \pi}{L} T\right)} = \cos{\left(\frac{\pi}{2}\right)}. $$

Porém, \cos{(x)} satisfaz a seguinte propriedade - \cos{(x)} = \sin{(x+\frac{3\pi}{2})}, ou seja, \sin{\left(2 \pi\right)}= - \cos{\frac{\pi}{2}}.

Daí, \sin{\left(\frac{n \pi}{L} T\right)} = \sin{\left(\frac{\pi}{2}\right)} , portanto $$\frac{n \pi}{L} = 2 \pi \Leftrightarrow T = \frac{2L}{n}.$$

OBSERVAÇÃO:

Note ainda que 2L também é período de \cos{\left(\frac{n \pi}{L} x\right)} e \sin{\left(\frac{n \pi}{L} x\right)}.

De fato, $$\cos{\left(\frac{n \pi}{L} (x+2L)\right)} = \cos{\left(\frac{n \pi}{L} x\right)} \cos{\left(2n\pi\right)}- \sin{\left(\frac{n \pi}{L} x\right)} \sin{\left(2n\pi\right)} = \cos{\left(\frac{n \pi}{L} x\right)}$$

Analogamente, comprovamos o mesmo fato para a função seno.

O período \frac{2L}{n} é denominado período mínimo de ambas as funções.

PROPRIEDADES DAS FUNÇÕES PERIÓDICAS

Seja f(x) uma função real periódica com período T. Então, podemos estabelecer as seguintes propriedades:

1. Para todo n \in \mathbb{Z}, temos que $$f(x+nT) = f(x).$$
2. Se f(x) e g(x) possuem período T, então $$h(x) = \alpha f(x) + \beta g(x); \;\;\;\;\;\alpha , \beta \in \mathbb{R}.$$

Leia Mais:

• O Delta de Dirac | Da definição à solução de Equações Diferenciais
• Função de Heaviside ou Degrau Unitário
• A Função Erro de Gauss ou Integral de Probabilidade
• Função Gama | Fatorial Generalizado e Gama Incompleta
• Desafios de Matemática: 11 problemas para desafiar sua mente
• Efeito Broboleta | Edward Lorenz e a Teoria do Caos