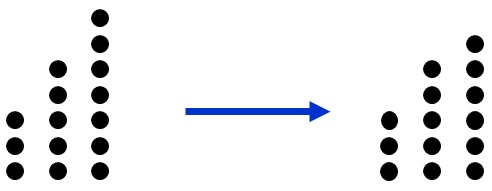
De qualquer posição insegura é possível jogar para uma posição segura. De uma posição segura, todas as jogadas possíveis conduzem a posições inseguras.
Quem Foi Bouton?
Bulletin of the American Mathematical Societycomo o nascimento da teoria dos jogos combinatórios.
O Teorema de Bouton e a Solução do Jogo do NIM
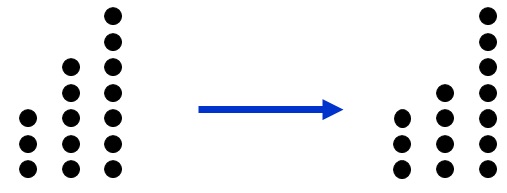
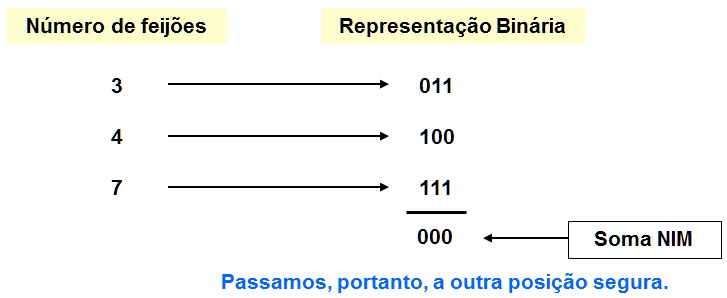
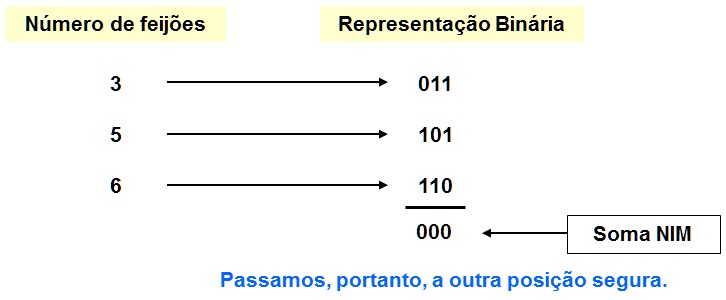
nimm
Exemplo do Jogo do NIM com pilhas de 3, 5 e 7 feijões
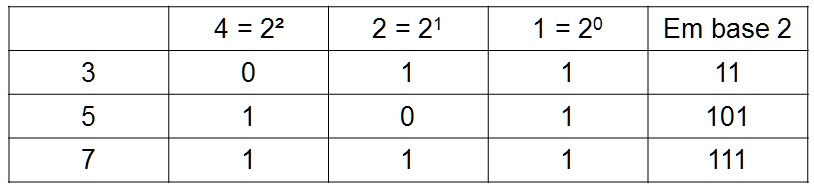
0 + 0 = 1 + 1 = 0
1 + 0 = 0 + 1 = 1
soma-nim3, 57
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
(011)+(101)+(111) = 001.
A posição acima, portanto, não é segura.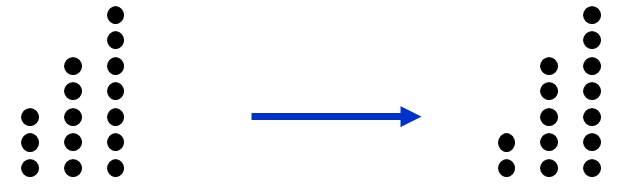
“Contos em Contas”
Leia Mais:
- TEORIA DOS JOGOS | Matemática Aplicada à Sociologia e Economia
- O Princípio das Gavetas de Dirichlet e o Jogo do SIM | Teoria dos Jogos
- Jogos Matemáticos | 6 Jogos Clássicos Envolvendo Matemática.
- Desafios de Matemática: Alguns problemas para desafiar sua mente!
- Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
